I.

Условие

Составить математическую модель линейной производственной задачи при возможном выпуске четырех видов продукции с использованием трех видов ресурсов, взяв исходные данные из приложения 1, где матрица удельных затрат А, вектор объема ресурсов В и вектор удельной прибыли С компактно записаны в виде

Преобразовать данную задачу к стандартному виду задачи линейного программирования и решить ее симплексным методом.

Дано:

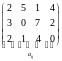- c_j (прибыль от реализации единицы товара),

- b_i – запас ресурсов

(количество i-го товара на производство

1 единицы j-го товара)

Сколько и какого товара нужно производить, чтобы прибыль была максимальной?

Решение

Пусть x_j – количество j-го товара.

Целевая функция имеет вид:

.

Введем ограничения, связанные с конечностью ресурсов:

.

Приведем к системе уравнений:

.

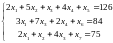Пусть x₅, x₆, x₇ – базисные переменные, х₁, х₂, х₃, х₄ – свободные.

Составим таблицу

	Своб.чл.	X1	X2	X3	X4	X5	X6	X7
X5	126	2	5	1	4	1	0	0
X6	84	3	0	7	2	0	1	0
X7	75	2	1	4	0	0	0	1
L	0	-26	-35	-18	-30	0	0	0

Выберем разрешающий столбец (наибольший по модулю отрицательный коэффициент в целевой функции), сделаем х₂ базисной переменной. Выберем разрешающую строку: т.к. 2,5<75, то разрешающей строкой будет строка х₅. Повторим эту операцию до тех пор, пока все коэффициенты в строке целевой функции не будут положительны.

	Своб.чл.	X1	X2	X3	X4	X5	X6	X7
X2	25,2	0,4	1	0,2	0,8	0,2	0	0
X6	84	3	0	7	2	0	1	0
X7	49,8	1,6	0	3,8	-0,8	-0,2	0	1
L	882	-12	0	-11	-2	7	0	0

	Своб.чл.	X1	X2	X3	X4	X5	X6	X7
X2	14	0	1	-3/4	1/2	1/5	-1/7	0
X1	28	1	0	2 1/3	2/3	0	1/3	0
X7	5	0	0	0	-1 7/8	-1/5	-1/2	1
L	1218	0	0	17	6	7	4	0

L_оптим=1218+17х₃+6х₄+7х₅+4х₆.

L_max=1218

Х₁ =28 – базисная переменная,

Х₂ =14 – базисная переменная,

Х₃ =0 – свободная переменная,

Х₄ =0 – свободная переменная,

Х₅ =0 – свободная переменная,

Х₆ =0 – свободная переменная,

Х₇ =5 – базисная переменная.

Вывод

Для того,чтобы прибыль была максимальной (=1218), необходимо производить 28 единиц первого товара, 14 единиц второго товара и 5 единиц - остаток 3-го ресурса.

II.