
- •23. Собственный механический и магнитный моменты электрона.
- •24 Полный механический и магнитный моменты электрона. Принцип Паули
- •25. Распределение электронов в атоме по состояниям. Таблица Менделеева.
- •7. Давление света.
- •8. Гипотеза де Броиля.Волновой пакет частиц.
- •11. Операторы.
- •12 Собственные волновые функции и собственные значения физических величин. Собственные волновые функции оператора компоненты импульса.
- •15 Уравнение Шредингера для свободной частицы.
- •Частица в одномерной потенциальной яме.
- •20. Линейный гармонический квантовый осциллятор
- •21. Классическая модель атома водорода
- •22. Уравнение Шредингера для водорода. Квантовые числа
- •43.Деление ядер
- •44.Плазма
- •9.Соотношение неопределенностей Гейзенберга.
- •10.Опыт Дэвиссона и Джермера. Смысл волн де Бройля
- •4.Гипотеза Планка. Вывод формулы Планка.
- •5.Внешний фотоэффект.
- •6.Эффект Комптона.
- •34. Эффективная масса электрона
- •35. Полупроводники. Собственная и примесная проводимость.
- •36. Полупроводниковый диод.
- •37. Эффект Зеебека. Эффект Пельтье.
- •38. Конт разн потенц Контакт металл-металл.
- •39. Атомное ядро и его характеристики.
- •40. Ядерные силы и их свойства.
- •41. Радиоактивность. Альфа-распад. Бета-распад.
- •42.Закон радиоактивного распада.
- •26 Механический и магнитный моменты атома. Ls-связь.
- •27 Понятия об энергетических уровнях молекул.
- •28.Рентгеновские спектры. Закон Мозли.
- •29. Принцип тождества микрочастиц
- •30. Электронный газ в одномерном случае. Энергия Ферми.
- •31. Распределение Ферми-Дирака
- •32. Распределение Бозе-Эйнштейна
- •33. Энергетические зоны кристалла
- •45. Термоядерный синтез
- •46. Цепная реакция
- •Особенности теплового излучения, его характеристики.
- •2 Законы Кирхгофа, Стефана-Больцмана, Вина.
- •3. Тепловое излучение. Формула Релея-Джинса.
- •17 Решение уравнение Шредингера для низкого потенциального барьера.
- •18 Решение уравнение Шредингера для высокого потенциального барьера.
- •19)Туннельный эффект
- •13. Принцип причинности. Общее уравнение Шрёдингера.
- •14.Уравнение Шредингера для стационарных состояний
9.Соотношение неопределенностей Гейзенберга.
В квантовой механике отсутствует понятие траектории. Если в классической механике можно одновременно определить место нахождения частицы и ее скорость, то в квантовой механике это невозможно. Чем точнее определяется координата частицы, тем больше неточность в определении ее импульса. Щель шириной ∆у. 1ый дифракционный максимум. Рассмотрим дифракцию электрона на щели. До того как электрон пройдет щель, проекция импульса эл-на на ось у=0. Координата у до пролета эл-ном щели не определена. В тот момент, когда эл-н проходит щель, неопределенность у становится ∆у. При прохождении эл-ном щели в рез-те дифракции, эл-н рассеивается. Наиболее вероятная область рассеивания эл-на – область 1-го дифракционного максимума, кот. огранич. 2 симметричными минимумами. В рез-те дифракции, импульс эл-на попадает в область, опр. углом 2 . В проекции импульса Ру появляется неопределенность равная ∆р=2p*sin . Условие главного дифракционного минимума имеет вид b*sin =mλ, m=±1;±2…; ∆у*sin =λ => sin =λ/∆y;
Подставим:
∆py=2p*
λ/∆y;
∆y∆
py=2ћkλ;
∆y∆py=2λћ*2π/λ;
∆y∆py=4πћ,
где 4πћ=const;
т.е. ∆y∆py=const;
точные соотношения неопределенностей
Гейзенберга имеют вид
 ;
;
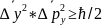 ;
;
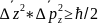 ;
при решении пользуются упрощенными:
∆x∆
;
при решении пользуются упрощенными:
∆x∆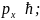 где ћ=h/2π;
∆y∆
где ћ=h/2π;
∆y∆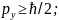 ∆x∆
∆x∆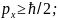
∆z∆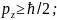 иногда используются соотношения вида
∆x∆
иногда используются соотношения вида
∆x∆
∆y∆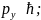 ∆z∆
∆z∆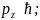 Существует еще одно соотношение ∆E*∆t~ћ.
Чем точнее надо измерить энергию, тем
больше времени надо затратить.
Существует еще одно соотношение ∆E*∆t~ћ.
Чем точнее надо измерить энергию, тем
больше времени надо затратить.
10.Опыт Дэвиссона и Джермера. Смысл волн де Бройля
Опыт Дэвиссона-Джермера — физический эксперимент по дифракции электронов, проведённый в 1927 г. американскими учёными Клинтоном Дэвиссоном и Лестером Джермером.
Идея опыта:
Проводилось
исследование отражения электронов от
монокристалла никеля. Установка включала
в себя монокристалл никеля, сошлифованный
под углом, и установленный на держателе.
На плоскость шлифа направлялся
перпендикулярно пучок монохроматических
электронов. Скорость электронов
определялась напряжением U
на электронной пушке:
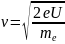 .
Под углом θ к падающему пучку электронов
устанавливался цилиндр Фарадея,
соединённый с чувствительным
гальванометром. По показаниям гальванометра
определялась интенсивность отражённого
от кристалла электронного пучка. Вся
установка находилась в вакууме.
.
Под углом θ к падающему пучку электронов
устанавливался цилиндр Фарадея,
соединённый с чувствительным
гальванометром. По показаниям гальванометра
определялась интенсивность отражённого
от кристалла электронного пучка. Вся
установка находилась в вакууме.
В опытах измерялась интенсивность рассеянного кристаллом электронного пучка в зависимости от угла рассеяния 0<θ<90o от азимутального угла 0<φ<360o , от скорости электронов в пучке.
Опыты показали, что имеется ярко выраженная селективность (выборочность) рассеяния электронов. При различных значениях углов и скоростей, в отражённых лучах наблюдаются максимумы и минимумы интенсивности. Условие максимума: ∆=2d*sinθ=λn, n=1,2..
Здесь
d—
постоянная кристаллической решётки.Таким
образом наблюдалась дифракция электронов
на кристаллической решётке монокристала.
Опыт явился блестящим подтверждением
существования у микрочастиц волновых
свойств. Правильное толкование волн
Дебройля дал Макс Борн. Волны Дебройля
имеют вероятностный смысл. Борн показал,
что интенсивность волны Дебройля
определяет вероятность нахождения
частицы в данный момент времени в данной
точке пространства. Ф-ция Дебройля
является сложной ф-цией координат и
времени и никакого отношения к волне
не имеет, но термин «волновая ф-ция»
сохранился. Интенсивность волны Дебройля
опр-ся Ψ*φ*=|Ψ|2.
это вероятность нахождения частицы в
данной точке пространства в данный
момент времени. Условие нормировки:
 Данное равенство говорит о том, что
частица точно находится в данный момент
времени в объеме V.
Данное равенство говорит о том, что
частица точно находится в данный момент
времени в объеме V.
