23. Собственный механический и магнитный моменты электрона.

Момент импульса электрона, движущегося по орбите, равен 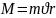(механический момент). Электрон движется по орбите создаёт магнитный момент 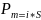S-площадь орбиты. За период T ч/з любое сечение орбиты пройдёт заряд 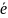, что соответствует току

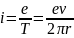
Найдём отношение магнитного момента к механическому

= ;

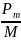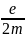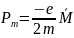
Эксперимент соотношения для атомов Fe привело к рез-ту, в 2 раза превысило результат, записанный выше: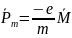

Этот факт привёл к предположению , что обладает собственным механическим и магнитным моментам. Основными экспериментами , подтверждающий этот факт являются опыты Штерна-Герлоха и спектры излучения цельных металлов.

1.Опыты Штерна-Герлоха атомы H , находится в S-сост. пропускаемый ч/з неоднородное магнитное поле, на атомы в неоднородное магнитное поле должна действовать сила , в том случае , если атомы обладают магнитным моментом 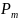, но в s – состоянии магнитное число m=0. В соответствии гиромагнитным соотношениям , нулевому мехоническому моменту e=0 соответствует нулевой магнитный момент.

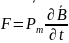
В S состоянии атом орбит механич и магнитными моментами не обладает т.е в опыте Штерна –Герлоха не должно было бы наблюдаться отклонение пучка атома H , тем не менее на экране наблюдался вместо однако пятна 2 (пучёк раздвоился)

Действие магнитного поля на пучёк в S- состоянии можно было объяснить , только предполож. , что атом обладает собст. магнитным моментом, кот. складывается из собственных моментов электронов.

Атом водорода имеет 1 электрон т.к. опыты Штерна- Герлоха привели к заключ., что обладает собственным магнитным моментом изависит от проекции этого момента . Расчит значение собственного магнитного момента электрона. Получим название магнетона Бора.

С собственным магнитным моментом связан собственный магнитный момен.-спин. Ярким подтверждением существованию собственн. магнитному и мех. моментов является спектры щелочных металлов в частном случае спектры Na, в котором вместо 1й линии, соотв переходу 2p->1S наблюдается две линии, соответствующие этому переходу.

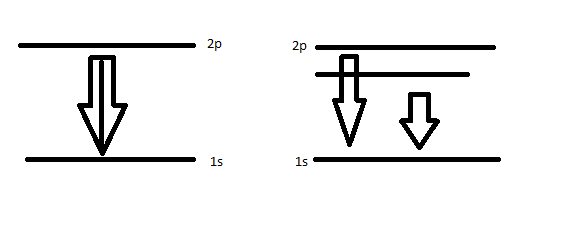
Состоянию p соответствует l=1. В этом случае магнитное число m принимает значения -1,0,1.

Вырожение по магнитному числу m, это выражение снимается в магнитном поле , в котором должно было бы наблюдаться 3 линии соответствующие значению m. Дуплет Na наблюдается и в отсутствии внешнего магнитного поля . Кроме того наблюдается 2 линии , а не 3. Наличие линий объясняется следующим образом: круговые токи в атомах создают слабое магнитное поле, которое оказывает воздействие на собственный магнитный момент электрона и в зависимости от его проекции на направление поля появляется 2 линии. Определим условие квантования механического момента.

Магнетон Бора опред. проекцию момента на некоторое направление. Воспользуемся соотношением для собственных моментов и подставим туда значения магнитона Бора : ;

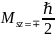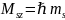; ; , то =>

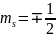
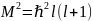
Магнитное число m связано с орбитальным числом , чтобы провести различие м/ у l и квантовым числом, определяющее условие квантования собственного мех момента, его обозначают буквой S , тогда условие квантования собственного мех момента запишется в виде , используем связь

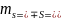S=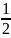

Условие квантования орбит механического момента :

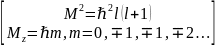
Условие квантования собств механического момента:

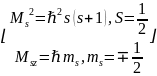
Каждое состояние характеризуется суммарным значение момента импульса: Полный момент импульса: , j= , j меняется от l+S до