46. Условия независимости криволинейного интеграла второго рода от пути. Интегрирование полных дифференциалов.
Пусть ф-ции P(x,y),Q(x,y) и их частные производные dP/dy, dQ/dx непрерывны, замкнуты, ограничены односвязной областью Д, тогда следующие 4 условия эквивалентны:
1)
,
где L
– любой замкнутый контур Д.
2)
не
зависит от пути AB.
3) Pdx+Qdy=dU, U – однозначная ф-ция, определенная в области Д. \
4) dP/dy=dQ/dx в области Д.
Доказательство:
где
.
Т.к. у ф-ции U существуют непрерывные частные произодные, то она дифиренцируема.
Нахождение ф-ции по ее полному дифференциалу.
Первый способ:
U(x,y)-?; dU=Pdx+Qdy; Pdx+Qdy*dQ/dx=dP/dy
Второй способ:
;
{
;
}
;
не зависит от пути.
48-49. Векторные поля. Поток векторного поля. Дивергенция.
Говорят, что в V
занадо векторное поле, если каждой т.
поставлен
в соответствие некоторый вектор
.
Физ. Векторные поля не зависят от выбора
СК.
Векторная линия – кривая, в каждой точке M которой направлен по касательной к кривой. Векторная трубка – часть пространства, состоящая из целых векторных линий, каждая ВЛ или целиком лежит внутри этой трубки или находится вне ее. Поток векторного поля. Дивергенция.
Дивиргенцией
векторного поля
называется
скалярная ф-ция
.Формула
Остроградского:
характеризует
плотность источников поля в данной
точке. Не зависит от выбора СК.
Циркуляция и ротор векторного поля.
Ротором (или вихрем)
векторного поля
называется вектор-функция
Ротор характеризует завихренность поля в данной точке. Ротор является постоянным вектором, направленным вдоль оси вращения OZ. Его модуль равен удвоенной угловой скорости вращения тела.
Рассмотрим
.
С- кусочно гладкая пов-ть. КРИ-2
называется циркуляцией
вдоль кривой L
в направлении
.
Если
-силовое
поле, то его циркуляция – работа вдоль
пути L.
(формула Стокса).
48. Потенциальное векторное поле и его свойства.
называется
потенциальным в области G,
если его можно представить как градиент
некоторого скалярного поля U(M).
Функция U(M)
– потенциал
векторного поля
.
;
;
;
;
;
Т.о. в потенциальной поверхностно односвязной области G поле обладает следубщими свойствами:
1) циркуляция потенциального вдоль любого замкнутого контура равна нулю.
2) Для любых т. А,В из области G циркуляция потенциального поля не зависит от выбора кривой АВ, а зависит только от выбора А и В.
3) Потенциальное поле является безвихревым
- необходимое и
достаточное условие потенциальности
поля
в поверхностно односвязной области.
Гармоническое векторное поле.
гармоноческое, если оно является одновременно потенциальным и сопеноидальным.
;
;
50. Формула Грина.
Область наз. односвязной если в ней любой замкнутый контур может быть стянут в точку с помощью непрерывной деформации, при к-й не границы области не пересекаютя.
Область D наз. односвяз., если каков бы ни был замкн. контур l , лежащий внутри этой области, ограниченная этим контуром конечн. часть пл-ти целиком принадл. D.
Порстая область: замкн. пл-ть D (обл. вместе с её границами) – её можно разбить на конечное число как y- так и x- трапецивидных областей.
Например: круг, прямоугольник, кольцо.
Теор. Грина: пусть
P(x,y),
Q(x,y)
и
и
непрерывны в простой области D
тогда
где L – граница области D, к-я обходится в положительном направлении.
Док-во
Предположим D – односвяз. область, огр. L – полож. ориентир. Предположим, что оюл. D такова, что прямые параллельн. осям пересекают ее не более, чем в 2-х точках.
Для I2 – аналогично.
Формула Грина имеет место для любой простой области.
Если контур обходится в обратном направлении, то перед двойным интегралом ставится «-».
51. Теорема Остроградского
Формула Остроградского – Грина устанавливает связь между криволинейным интегралом и двойным интегралом, т.е. дает выражение интеграла по замкнутому контуру через двойной интеграл по области, ограниченной этим контуром.
Будем считать, что рассматриваемая область односвязная, т.е. в ней нет исключенных участков.
y
y = y2(x)
D
A
C
B
y= y1(x)
0 x1 x2 x
Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде:
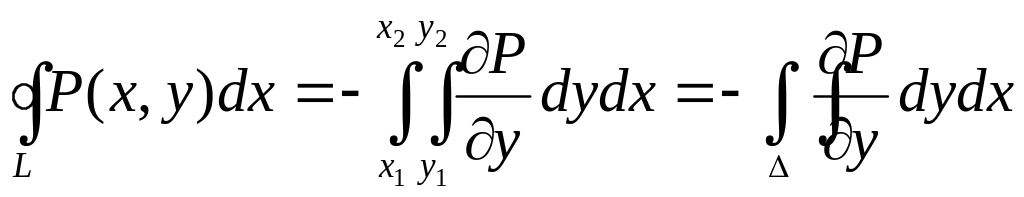
Если участки АВ и CD контура принять за произвольные кривые, то, проведя аналогичные преобразования, получим формулу для контура произвольной формы:
Формула Остроградского – Грина справедлива и в случае многосвязной области, т.е. области, внутри которой есть исключенные участки. В этом случае правая часть формулы будет представлять собой сумму интегралов по внешнему контуру области и интегралов по контурам всех исключенных участков, причем каждый из этих контуров интегрируется в таком направлении, чтобы область все время оставалась по левую сторону линии обхода.
Формула Остроградского – Грина позволяет значительно упростить вычисление криволинейного интеграла. Криволинейный интеграл не зависит от формы пути, если он вдоль всех путей, соединяющих начальную и конечную точку, имеет одну и ту же величину. Условием независимости криволинейного интеграла от формы пути равносильно равенству нулю этого интеграла по любому замкнутому контуру, содержащему начальную и конечную точки. Это условие будет выполняться, если подынтегральное выражение является полным дифференциалом некоторой функции, т.е. выполняется условие тотальности.
52. Формула стокса
Формула Стокса связывает криволинейные интегралы второго рода с поверхностными интегралами второго рода.
Пусть в пространстве задана некоторая поверхность S. L – непрерывный кусочно – гладкий контур поверхности S.
z S
L
y
l
x
Предположим, что функции P,Q и R непрерывны на поверхности S вместе со своими частными производными первого порядка. Применим формулу, выражающую криволинейный интеграл через определенный.
Введем обозначения:
Применив формулу Грина – Остроградского, можно заменить криволинейный интеграл равным ему двойным интегралом. После преобразований устанавливается следуюшее соответствие между криволинейным и поверхностным интегралом:
эта формула и называется формула Стокса.