26. Линейные ду 1 порядка: однор и неоднор, метод Бернули

Определение. Ду линейное относительно неизвестной функции и ее производной, если оно может быть записано в виде:

при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением. P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b.

ЛОДУ. Рассмотрим методы нахождения общего решения ЛОДУ 1 порядка вида .

Общее решение:

ЛНДУ Для интегрирования линейных неоднородных уравнений (Q(x)0) применяются в основном два метода: метод Бернулли и метод Лагранжа. Метод Бернулли. Суть метода: искомая функция представляется в виде произведения двух функций .При этом - диф-е по частям. Подставляя в исходное уравнение, получаем: т.к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, может быть произвольным, выбранным по нашему усмотрению. Т.о., можно одну из составляющих произведение функций выбрать так, что выражение .возможно получить функцию u, проинтегрировав соотношение как однородное ду: Для нахождения v подставим поученное выражение для u в исходное уравнение с учетом того, что выражение, стоящее в скобках, равно нулю.

Интегрируя, можем найти функцию v:

; ; вторая составляющая произведения Подставляя полученные значения, получаем: Окончательно: , С₂ - произвольный коэффициент.

Метод Лагранжа.

Метод Лагранжа решения неоднородных линейных дифференциальных уравнений еще называют методом вариации произвольной постоянной. Вернемся к поставленной задаче:

Первый шаг - отбрасываем правую часть уравнения и заменим ее нулем. Далее находится решение получившегося однородного ду: .

Для того, чтобы найти соответствующее решение неоднородного дифференциального уравнения, будем считать постоянную С₁ некоторой функцией от х.

Тогда по правилам дифференцирования произведения функций получаем:

Подставляем полученное соотношение в исходное уравнение

Из этого уравнения определим переменную функцию С₁(х):

Интегрируя, получаем:

Подставляя это значение в исходное уравнение, получаем:

.

Таким образом, мы получили результат,

Уравнением Бернулли называется уравнение вида

где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.

29. ЛДУ-n: однор и неоднор Линейный диф опер-р его св-ва, св-св реш ЛДУ.

Опр. ЛДУ n – го порядка называется любое Ур-е первой степени отн-но ф-ии у и ее производных вида: где p₀, p₁, …,p_n – функции от х или постоянные величины, причем p₀  0. Левую часть этого Ур-я обозначим L(y). Опр. Если f(x) = 0, то ур-е L(y) = 0 называется ЛОДУ, если f(x)  0, то уравнение L(y) = f(x) называется ЛНДУ, если все коэффициенты p₀, p₁, p₂, … p_n – постоянные числа, то уравнение L(y) = f(x) называется линейным ДУ высшего порядка с постоянными коэффициентами.

Линейные однородные дифференциальные уравнения с произвольными коэффициентами.

Рассмотрим уравнение вида Опр. Выражение называется линейным дифференциальным оператором.Линейный дифференциальный оператор обладает следующими свойствами: 1) 2)

Решения линейного однородного уравнения обладают следующими свойствами: 1) Если функция у₁ является решением уравнения, то функция Су₁, где С – постоянное число, также является его решением. 2) Если функции у₁ и у₂ являются решениями Ур-я, то у₁ +у₂ также является его решением.

Структура общего решения. Общее решение ЛОДУ второго порядка. Из вышеизложенного видно, что отыскание общего решения ЛОДУ сводится к нахождению его фундаментальной системы решений.

Однако, даже для уравнения второго порядка, если коэффициенты р зависят от х, эта задача не может быть решена в общем виде.

Тем не менее, если известно одно ненулевое частное решение, то задача может быть решена.Теорема. Если задано уравнение вида и известно одно ненулевое решение у = у₁, то общее решение может быть найдено по формуле:

31.метод вариации произвольных постоянных.

Для этого сначала находят общее решение соответствующего однородного уравнения в виде:

Затем, полагая коэффициенты C_i функциями от х, ищется решение неоднородного уравнения:

Можно доказать, что для нахождения функций C_i(x) надо решить систему уравнений:

33. Двойные интегралы. Св-ва.С учетом того, что S_i = x_i  y_i получаем:

В приведенной выше записи имеются два знака , т.к. суммирование производится по двум переменным х и у.

Т.к. деление области интегрирования произвольно, также произволен и выбор точек Р_i, то, считая все площади S_i одинаковыми, получаем формулу:

Свойства двойного интеграла.

1)

2)

3) Если  = ₁ + ₂, то

4) Теорема о среднем. Двойной интеграл от функции f(x, y) равен произведению значения этой функции в некоторой точке области интегрирования на площадь области интегрирования.

5) Если f(x, y)  0 в области , то .

6) Если f₁(x, y)  f₂(x, y), то .

7) .

36-37. Замена переменных в двойном интеграле. Двойной интеграл в полярной системе координат.

(*)

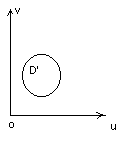
Свойства

1. x(u,v), y(u,v) – взаимно однозначны

2. x(u,v), y(u,v) – непрерывные, непр. частн. пр-е 1-го порядка

3. 

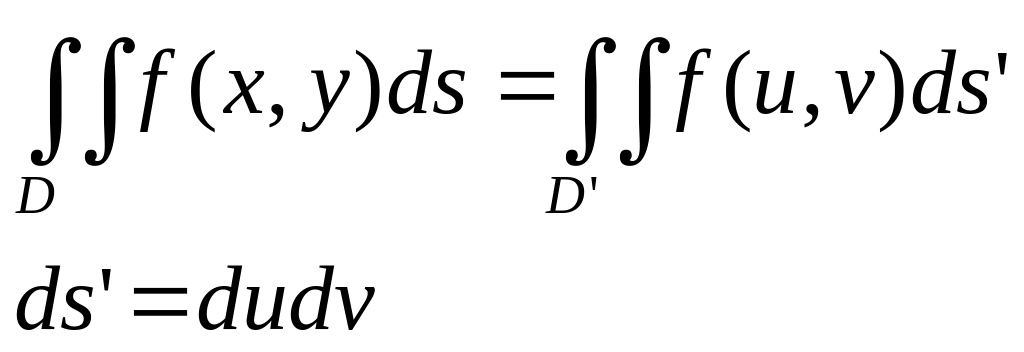
P₁: x(u,v), y(u,v) P_2: x(u+_∆u,v), y(u+_∆u,v)

I – Якобиан(Якоби)

Модуль I – коэффициет растяжения площади в т. с координатами u и v при отображении D на D’.

Вычисление в полярной сист координат. ,

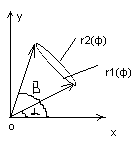
a)

b )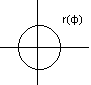

c)

39. Тройной интеграл: определение, свойства.

Пусть задано пространств. тело D. В точках этого тела определена ф-ция U=f(x,y,z). Разобьем это тело на конечное число D_i –тых (i=1,2,3,…). В каждой области D_i выберем произвол. точку (x_i,y_i,z_i) и составим интегральную _n= (x_i,y_i,z_i) * V_i Если сущ. предел и он конечный и он не зависит от способа деления обл. D на части и выбора точек (x_i,y_i,z_i) , то этот предел называют тройным интегралом по обл.D от ф-ции f(x,y,z) lim(_n= f(x,y,z)dx dy dz Следовательно m=(x,y,z)dxdydz

Св-ва тройного интеграла аналогично св-м двойного интеграла 1) Всякая интегрируемая в обл. D ф-ция ограничена в этой области.

2) Могут быть построены суммы Дарбу

верх S_= M_i * V_i низ s_= m_i * V_i

3) Необходимо и достаточное условие сущ. интеграла

lim( S_-s_)=0

4) Как и в случае двойного интеграла сущ. тройной интеграл от любой непрерывной ф-ции, заданной в обл. D. Однако тройной интеграл сущ. и в случае, когда ф-ция f(x,y,z) имеет разрывы 1-го рода на конечном числе пов-тей данного тела D.

5)Тройной интеграл обладает св-вами линейности и аддетивности

_Dfdx = _D1fdx + _D2 , где D=D1D2

6)Если сущ. тройной интеграл от ф-ции f, то сущ. интеграл по модулю

и существует равенство

fdv

Если функция fв области D ограничена какими-то числами m  f  М , то для тройного интеграла справидливо неравенство

mV_d  dvM V_D

7) Имеет место теорема о среднем , т.е. если функция (x,y,z) не-прерывная в области D , то справедливо равенство

 dv   (X₀ , Y_o , Z₀) (X₀ , Y_o , Z₀)D

40. Вычисление тройных интегралов

Определение: Тройным интегралом f(M) по обл. Ω € R называется предел интегральной суммы

∑_k=1ⁿf(M_k)∆V_k = ∑_k=1ⁿf(ξ_k n_k ζ_k)V(Ω_k), если мелкость разбиения обл. Ω λ = max d(Ω_k) стремится к 0.

Единственное отличие от ДИ заключается в том, что при нахождении тройного интеграла интегрирование ведется не по двум, а по трем переменным, а областью интегрирования является не часть плоскости, а некоторая область в техмерном пространстве.

Суммирование производится по области v, которая ограничена некоторой поверхностью (x, y, z) = 0.

Здесь х₁ и х₂ – постоянные величины, у₁ и у₂ – могут быть некоторыми функциями от х или постоянными величинами, z₁ и z₂ – могут быть функциями от х и у или постоянными величинами.

Пример. Вычислить интеграл

41. Замена переменных в тройных интегралах.

Операция замены переменных в тройном интеграле аналогична соответсвующей операции для двойного интеграла.

Можно записать:

,

где |i| - модуль Якобина.

38-42. Приложения двойных и тройных интегралов:

7) Вычисление объемов тел с помощью тройного интеграла.

Если поверхность тела описывается уравнением f(x, y, z) = 0, то объем тела может быть найден по формуле: при этом z₁ и z₂ – функции от х и у или постоянные, у₁ и у₂ – функции от х или постоянные, х₁ и х₂ – постоянные.

8) Координаты центра тяжести тела.

9) Моменты инерции тела относительно осей координат.

10) Моменты инерции тела относительно координатных плоскостей.

11) Момент инерции тела относительно начала координат.

В приведенных выше формулах п.п. 8 – 11 r – область вычисления интеграла по объему, w – плотность тела в точке (х, у, z), dv – элемент объема

• в декартовых координатах: dv = dxdydz;

• в циллиндрических координатах: dv = dzdd;

• в сферических координатах: dv = ²sinddd.

12) Вычисление массы неоднородного тела. Теперь плотность w – величина переменная.

1) Вычисление площадей в декартовых координатах.

Площадь S может быть вычислена с помощью двойного интеграла по формуле:

2) Вычисление площадей в полярных координатах.

43. Криволинейные интегралы I рода.

Определение. Кривая ( ) называется непрерывной кусочно – гладкой, если функции ,  и  непрерывны на отрезке [a,b] и отрезок [a,b] можно разбить на конечное число частичных отрезков так, что на каждом из них функции ,  и  имеют непрерывные производные, не равные нулю одновременно.

Если определено не только разбиение кривой на частичные отрезки точками, но порядок этих точек, то кривая называется ориентированнной кривой. Ориетированная кривая называется замкнутой, если значения уравнения кривой в начальной и конечной точках совпадают.

Рассмотрим в пространсве XYZ кривую АВ, в каждой точке которой определена произвольная функция .

Разобьем кривую на конечное число отрезков и рассмотрим произведение значения функции в каждой точке разбиения на длину соответствующего отрезка. Сложив все полученные таким образом произведения, получим так называемую интегральнуюсумму функции f(x, y, z).

Определение. Если при стремлении к нулю шага разбиения кривой на частичные отрезки существует предел интегральных сумм, то этот предел называется криволинейным интегралом от функции f(x, y, z) по длине дуги АВ или криволинейным интегралом первого рода.