12. Определенный интеграл с переменным верхним пределом.

Интеграл вида f(t)dt=Ф(x), x [a,b] – интеграл с перем. верхним пределом.

Теорема 1: пусть f(x) непрерыв. на [a,b], тогда Ф(х)= f(t)dt тоже непрерыв. на [a,b]

Док-во: х [a,b] возьмем (х+ х) [a,b]. Рассмотрим Ф(х)=Ф(х+ х)-Ф(х)= f(t)dt- f(t)dt= f(t)dt+ f(t)dt- f(t)dt= f(t)dt=f( ) х, где [х, х+ х].

Ф(х)=f( ) х.

х 0 => Ф(х) 0, что означает непрерывность Ф(х) в точке х.

т.к. х – любое, то Ф(х) непрерыв. на [a,b]. ч.т.д.

Теорема 2 (т. Барроу):пусть f(x) непрер. на [a,b], тогда Ф(х)= f(t)dt явл. первообразной для f(x) на [a,b], т.е. ( f(t)dt)=f(x)

Производная от интеграла с перем. верхним пределом равна подинтегр. ф-ции от перем. предела.

Док-во: Ф(х)=f( ) х, где [х, х+ х]

( f(t)dt)=Ф (x)=lim _{х 0} Ф(х)/ х= lim _{х 0} f( ) х/ х= lim _{х 0} f( ) (тогда х) =f(x) ч.т.д

f(х)dх= f(t)dt+С

13. формула Н.-Л.

Теорема: (Теорема Ньютона – Лейбница)

Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то

это выражение известно под названием формулы Ньютона – Лейбница.

Доказательство: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция 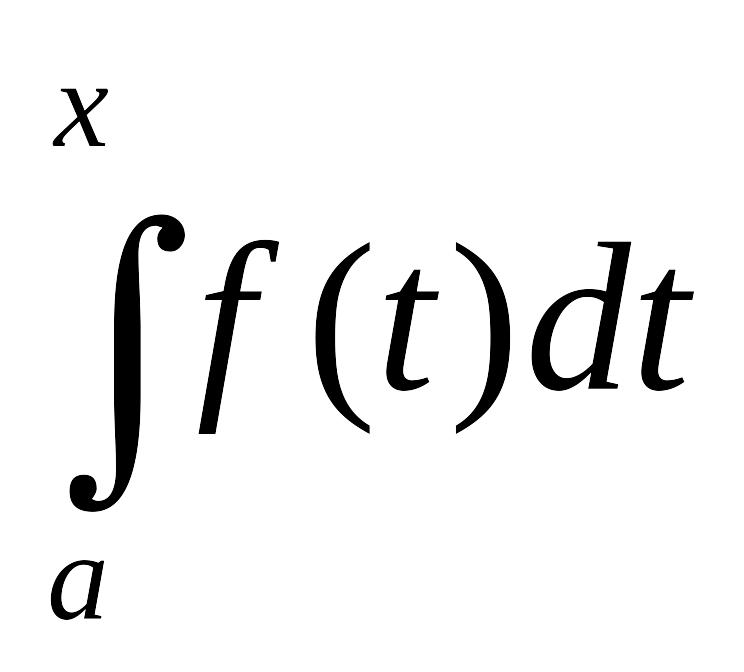- первообразная функция от f(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то

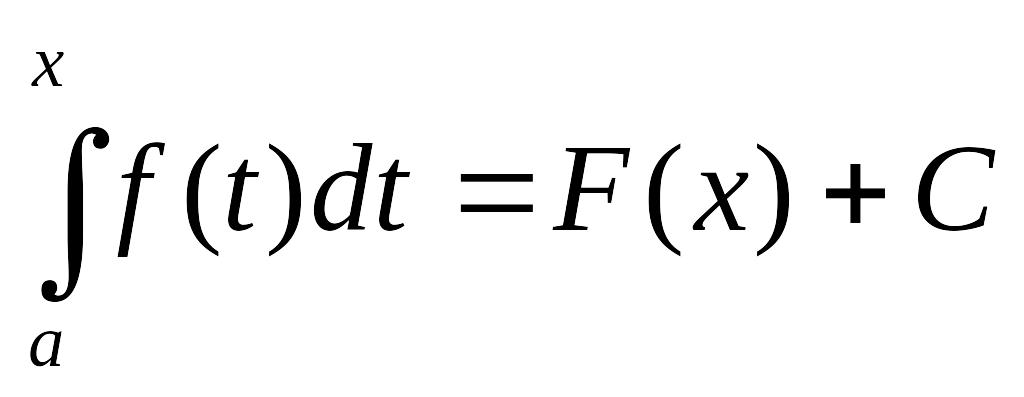
при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:

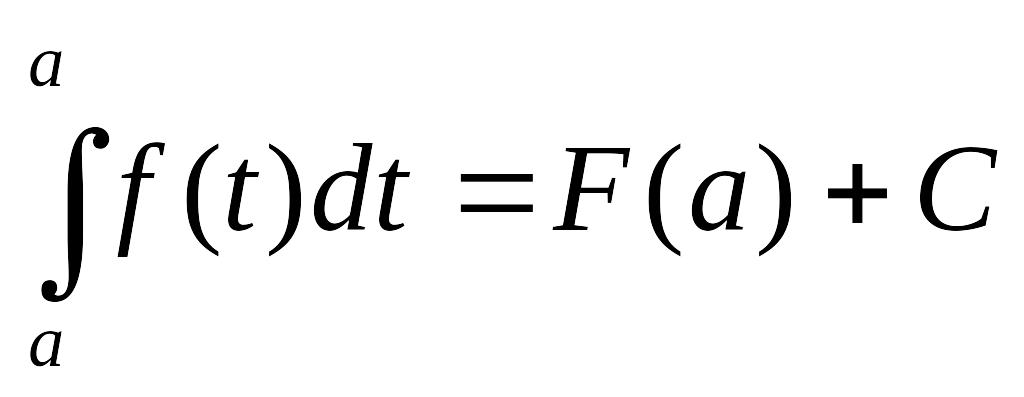
Тогда . А при х = b:

Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:

Теорема доказана.

Иногда применяют обозначение F(b) – F(a) = F(x) .

Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.

14. Замена переменных в определенном интеграле.

Теорема 1 (внесение множителя под знак дифференциала): Пусть u=(x) непрер. дифференцируема на пром-ке с концами a и b; пусть f(u) непрер. на множ-ве значений u=(x) Е().

Тогда f((x)) (х)dx= f(u)du

Док-во: если f(u) имеет первообр. F(u), то f((x)) (х) имеет первообр. F( (x))

f((x)) (х)dx= F( (x)) |^b_a= F( (b)) - F( (a)); f(u)du=F(u) |^(b)_(a)= F( (b)) - F( (a)) ч.т.д.

Теорема 2 (вынесение множителя из-под знака диф-ла): Пусть х=(t) непрер. диф-ма на (,); (t)>0 (=> возрастает) ((t)<0); ()=a; ()=b; пусть f(x) непрер. на пром-ке с концами a и b, тогда

f(х)dх= f((t)) (t)dt

Док-во: g(t)= f((t)) (t); если g(t) имеет первообр. G(t) на (a,b), то f(x) имеет первообр. F(x)=G(^-1(x)) (сущ-ние ^-1(x) гарантировано монотонностью: ^-1(x)>0 (<0)); f((t)) (t)dt= G(t) |^_=G() – G()

f(х)dх=G(^-1(x)) |^b_a=G(^-1(b)) - G(^-1(a))= G() - G() ч.т.д.

15. Интегралы от периодических, нечетных и четных ф-ций.

Теорема: Пусть f(x) интегр. на [-a,a], тогда если f(x) четная, то , если нечетная, то .

Если f(x) – непрерывная с периодом T, интегрируемая на некотором отрезке длины Т, то она интегрируема на любом отрезке длины Т.

Док-во:

Интегрирование по частям в определенном интеграле.

- непр. диф-е ф-ции на

; ; ;

16. НИ-1

Пусть f(x) определена на и инт на ; , т.е.

Пусть . Если этот lim существует и конечен, то говорят, что НИ-1 сходится. Если не существует или бесконечен, то расходится.

;

1. Аддитивность : Если сходится, то , ;

2. Линейность: Если сходится и 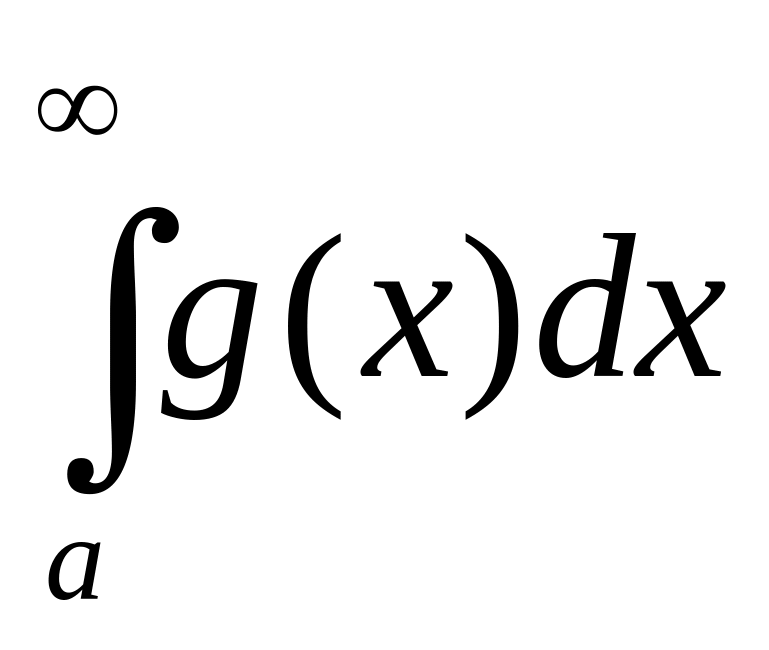сходится, то сходится и

Вычисление и преобразование НИ-1.

Если f(x) непрерывна на и F – какая-то первообразная для ф-ции f(x), то

Интегрирование по частям.: Если U,V – непрер. Диф-мы ф-ции на , то

Исследование на сходимость.

Т1: Пусть ф-ции f(x) и g(x) , тогда если и , то

сходится сходится

расходится пасходится

Предельный признак сравнения для НИ-1.

Т2: Пусть , ; , тогда если конечный , то и сходятся или расходятся одновременно.

При k=1 при

Т3: Если и сходится, то сходится.

Определение: называется абсолютно сходящимся, если сходится .

Если расходится, а сходится, от - неабсолютно (условно) сходящийся

Главное значении.

, , Если и сходится, то и