18. Построение статистической функцией распределения. Гистограмма.Назовите числовые характеристики статистического распределения. Дайте определение этих характеристик.
Статистическое распределение выборки
Пусть из генеральной
совокупности извлечена выборка, причем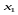
наблюдалось
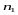раз,
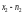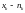раз ,
раз,
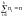— объем выборки.
Наблюдаемые
значения
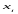называют вариантами,
а последовательность вариант, записанных
в возрастающем порядке — вариационным
рядом. Числа наблюдений называют
частотами,
а их отношения к объему выборки
—
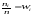относительными
частотами.
Статическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
Полигон и гистограмма
Полигоном частот
называют ломаную, отрезки которой
соединяют точки
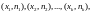.Для
построения полигона частот на оси
абсцисс откладывают варианты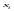
,
а на оси ординат — соответствующие им
частоты
.
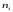Точки
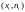соединяют отрезками прямых и получают
полигон частот.
Полигоном
относительных частот
называют ломаную, отрезки которой
соединяют точки
.
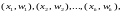Гистограммой
частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною h,
а высоты равны отношению
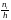(плотность частоты).
Для построения
гистограммы частот на оси абсцисс
откладывают частичные интервалы, а над
ними проводят отрезки, параллельные
оси абсцисс на расстоянии
.
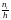Площадь i-го
участка гистограммы равна
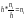— Сумме частот вариант i-го
интервала. Площадь гистограммы частот
равна объему выборки.
Гистограммой
относительных частот называют ступенчатую
фигуру, состоящую из прямоугольников,
основаниями которых служат частичные
интервалы длиною h,
а высоты равны отношению
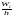— (плотность относительной частоты)
Площадь i-го
участка гистограммы равна
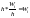—относительной частоте вариант i-го
интервала. Площадь гистограммы частот
равна сумме относительных частот
вариант, т.е. единице.
Статистические оценки параметров распределения
Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Естественно возникает задача оценки параметров, которыми определяется это распределение. Например, если наперед известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить (приближенно найти) математическое ожидание и среднее квадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение.
Обычно в распоряжении
исследователя имеются лишь данные
выборки, например, значения количественного
признака
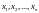полученные в результате n
наблюдений. Через эти данные и выражают
оцениваемый параметр.
Рассматривая
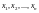как независимые случайные величины
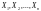можно сказать, что найти статистическую
оценку неизвестного параметра
теоретического распределения — это
значит найти функцию от наблюдаемых
случайных величин, которая и дает
приближенное значение оцениваемого
параметра.
Итак, статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.