8. Числовые характеристики вариационного ряда. Характеристики положения и характеристики рассеивания. Мода, Медиана. Размах варьирования. Коэффициент вариации. Асимметрия. Эксцесс.

Пусть изучается дискретная генеральная совокупность относительно количественного признака X.

Генеральной средне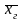й называют среднее арифметическое значений признака генеральной совокупности.

Если все значения x₁, х₂, …, x_N признака генеральной совокупности объема N различны, то

.

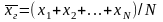Если же значения признака x₁, х₂, …, x_k имеют соответственно частоты N₁, N₂, ..., N_k , причем N₁ +N₂+…+N_k=N ,то

,

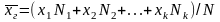т. е. генеральная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам.

Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема п.

Выборочной средне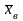й называют среднее арифметическое значение признака выборочной совокупности.

Если все значения x₁, х₂, …, x_n признака выборки объема n различны, то

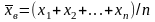
Если же значения признака x₁, х₂, …, x_k имеют соответственно частоты n₁, n₂, …, n_k, причем п₁ + п₂+… + n_k = n, то

,

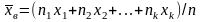или

,

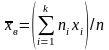т.е. выборочная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам.

Допустим, что все значения количественного признака X совокупности, безразлично-генеральной или выборочной, разбиты на несколько групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти ее среднюю арифметическую.

Групповой средней называют среднее арифметическое значений признака, принадлежащих группе.

Теперь целесообразно ввести специальный термин для средней всей совокупности.

Общей средне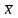й называют среднее арифметическое значений признака, принадлежащих всей совокупности.

Зная групповые средние и объемы групп, можно найти общую среднюю: общая средняя равна средней арифметической групповых средних, взвешенной по объемам групп,

Опуская доказательство, приведем иллюстрирующий пример.

Пример. Найти общую среднюю совокупности, состоящей из следующих двух групп:

Группа……………………....	первая		вторая
Значение признака…………	1	6	1	5
Частота……………………...	10	15	20	30
Объем……………………….	10+15 = 25		20 + 30 = 50

Решение. Найдем групповые средние:

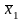=(10*1+15*6)/25=4;

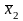= (20*1+30*5)/50 = 3,4.

Найдем общую среднюю по групповым средним:

=(25* 4 + 50*3,4)/(25 + 50) = 3,6.

Замечание. Для упрощения расчета общей средней совокупности большого объема целесообразно разбить ее на несколько групп, найти групповые средние и по ним общую среднюю.

Рассмотрим совокупность, безразлично-генеральную или выборочную, значений количественного признака X объема n:

значения признака .…… x₁ x₂ … x_k

частоты........................... n₁ n₂ … n_k

При этом 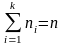. Далее для удобства записи знак суммы 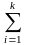заменен знаком .

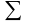Найдем общую среднюю:

.

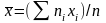Отсюда

. (*)

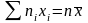Заметим, что поскольку x - постоянная величина, то

. (**)

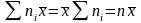Отклонением называют разность 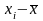между значением признака и общей средней.

Теорема. Сумма произведений отклонений на соответствующие частоты равна нулю:

.

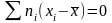Доказательство. Учитывая (*) и (**), получим

.

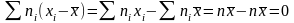Следствие. Среднее значение отклонения равно нулю.

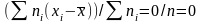
Пример. Дано распределение количественного признака X:

x_i 1 2 3

n_i 10 4 6

Убедиться, что сумма произведений отклонений на соответствующие частоты равна нулю.

Решение. Найдем общую среднюю:

= (10*1+4*2+6*3)/20 =1,8

Найдем сумму произведений отклонений на соответствующие частоты:

.

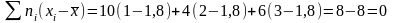Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику - генеральную дисперсию.

Генеральной дисперсией D_г называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения .

Если все значения x₁, х₂, …, x_N признака генеральной совокупности объема N различны, то

.

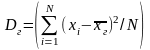Если же значения признака x₁, х₂, …, x_k имеют соответственно частоты N₁, N₂,…, N_k, причем N₁ +N₂+…+N_k=N, то

,

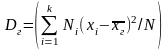т.е. генеральная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.

Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:

.

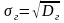Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения , вводят сводную характеристику - выборочную дисперсию.

Выборочной дисперсией 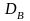называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения x₁, х₂, …, x_n признака выборки объема п различны, то

.

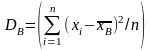Если же значения признака x₁, х₂, …, x_k имеют соответственно частоты п₁, n₂,…, n_k, причем n₁ + n₂+…+n_k = n, то

,

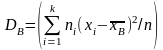т.е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.

Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой-средним квадратическим отклонением.

Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии:

.

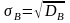Кроме выборочной средней и выборочной дисперсии применяются и другие характеристики вариационного ряда. Укажем главные из них.

Модой М₀ называют варианту, которая имеет наибольшую частоту. Например, для ряда

варианта ....1 4 7 9

частота .... 5 1 20 6

мода равна 7.

Медианой т_е называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т.е. n = 2k+ 1, то m_е=x_k+1 при четном n = 2k медиана

Например, для ряда 23567 медиана равна 5; для ряда 235679 медиана равна (5 + 6)/2 = 5,5.

Размахом варьирования R называют разность между наибольшей и наименьшей вариантами:

R=x_max-x_min

Например, для ряда 1 3456 10 размах равен 10 — 1 =9.

Размах является простейшей характеристикой рассеяния вариационного ряда.

Средним абсолютным отклонением θ называют среднее арифметическое абсолютных отклонений:

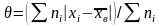
Например, для ряда

х_i 1 3 6 16

n_i 4 10 5 1

имеем:

;

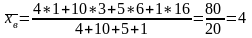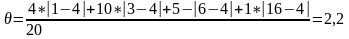
Среднее абсолютное отклонение служит для характеристики рассеяния вариационного ряда.

Коэффициентом вариации V называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней:

.

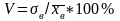Коэффициент вариации служит для сравнения величин рассеяния по отношению к выборочной средней двух вариационных рядов: тот из рядов имеет большее рассеяние по отношению к выборочной средней, у которого коэффициент вариации больше. Коэффициент вариации — безразмерная величина, поэтому он пригоден для сравнения рассеяний вариационных рядов, варианты которых имеют различную размерность, например если варианты одного ряда выражены в сантиметрах, а другого — в граммах.

Замечание. Выше предполагалось, что вариационный ряд составлен по данным выборки, поэтому все описанные характеристики называют выборочными; если вариационный ряд составлен по данным генеральной совокупности, то характеристики называют генеральными.

Для оценки отклонения эмпирического распределения от нормального используют различные характеристики, к числу которых относятся асимметрия и эксцесс. Смысл этих характеристик аналогичен смыслу асимметрии и эксцесса теоретического распределения.

Асимметрия эмпирического распределения определяется равенством

,

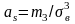где m₃ - центральный эмпирический момент третьего порядка.

Эксцесс эмпирического распределения определяется равенством

,

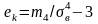где m₄ — центральный эмпирический момент четвертого порядка.

Моменты т₃ и m₄ удобно вычислять методом произведений.