32. Сравнение двух вероятностей биномиальных распределений.

Пусть в двух генеральных совокупностях производятся независимые испытания: в результате каждого испытания событие А может появиться в первой совокупности с неизвестной вероятностью P1, а во второй—с неизвестной вероятностью Р2. По выборкам, извлеченным из первой и второй совокупностей, найдены соответственные частоты:

W1(A)=m1/n1 W2{A) = m2/n2,

где m1,m2 — числа появлений события А; n1,n2 — количества испытаний.

В качестве оценок неизвестных вероятностей примем относительные частоты: P1=w1 и P2=w2.

Требуется при заданном уровне значимости а(альфа) проверить нулевую гипотезу, состоящую в том, что

вероятности Р1 и Р2 равны между собой: Н0: P 1 = P 2. Другими словами, требуется установить, значимо или незначимо различаются относительные частоты W1 и W2.Предполагается, что выборки имеют достаточно большой объем.

Правило 1. Для того чтобы при заданном уровне значимости а (альфа) проверить нулевую гипотезу H0: p1| = p 2 = p ,о равенстве вероятностей появления события в двух генеральных совокупностях (имеющих биномиальные распределения) при конкурирующей гипотезе Н1: Р1=\ Р2, надо вычислить наблюдаемое значение критерия:

U_набл=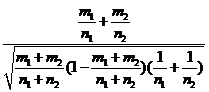

и по таблице функции Лапласа найти критическую точку Uкp по равенству Ф(Uкр.) = ( 1—а ) / 2.

Если | Uнабл. | < Uкр — нет оснований отвергнуть нулевую гипотезу.

Если | Uнабл. | > Uкр — нулевую гипотезу отвергают.

Правило 2. При конкурирующей гипотезе H1: p1 > р2 находят критическую точку правосторонней критической области по равенству ф(Ukр) = ( 1—2 а ) / 2.

Если Uнабл < Uкр — нет оснований отвергнуть нулевую гипотезу.

Если Uнабл > Uкр—нулевую гипотезу отвергают.

Правило 3.

При конкурирующей гипотезе H1: P1 < Р2 находят критическую точку Uкр. правилу 2, а затем полагают границу левосторонней критической области U кр== — Uкр.

Если Uнабл >—Uкр— нет оснований отвергнуть нулевую гипотезу.

Если Uнабл <—Uкр — нулевую гипотезу отвергают.

33.Сравнение нескольких дисперсий нормальных генеральных совокупностей по выборкам различного объемы. Критерий Бартлетта.

Пусть генеральные совокупности Х1, Х2, . . . , XL распределены нормально. Из этих совокупностей извлечены независимые выборки, вообще говоря, различных объемов Ni .По выборкам найдены исправленные выборочные дисперсии S1, S2, . . . , Sl(все S в квадрате). Требуется при уровне значимости а(альфа)проверить нулевую гипотезу об однородности дисперсий, т. е. гипотезу о равенстве между собой генеральных дисперсий:

Н₀: D(X₁)=D(X₂) =D(X₃)=… =D(X_l)

Введем обозначения

k_i=n_i-1 – число степеней свободы дисперсии S²_i/

k= – сумма чисел степеней свободы

– средняя арифметическая исправленных дисперсий,взвешенная по числам степеней свободы;

V=2.303( )

C=1+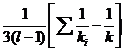

B= – случайная величина (критерий Бартлетта)

Наблюдаемое значение критерия : B_набл=  

И по таблице критических точек распределения   по уровню значимости   и числу степеней свободы l-1 (l– число выборок). Найти критическую точку   правосторонней критической области.

Если B_набл<  – нет оснований отвергнуть нулевую гипотезу.

Если B_набл>  – отвергаем нулевую гипотезу.

1)Критерий Бартлетта  весьма чувствителен к отклонениям распределения от нормального, поэтому к выводам, полученным по этому критерию надо относиться осторожно.2)При условии однородности дисперсий в качестве оценки генеральной дисперсии принимают среднюю арифметическую исправленных дисперсий, взвешенную по числам степеней свободы.