2) Найти асимптотическое поведение спектра энергии треугольного сигнала вида при больших частотах, не вычисляя его спектр.

Для треугольного сигнала (2.5) расчет показывает, что

(2.26)

Здесь спектр спадает при увеличении частоты пропорционально четвертой степени.

Билет 8

1) Функция автокорреляции действительного детерминированного сигнала. Взаимная функция корреляции двух действительных детерминированных сигналов.

Наряду со спектральной характеристикой сигналов часто используется корреляционный анализ сигналов. Корреляционная (или автокорреляционная) функция сигнала определяется для детерминированных вещественных сигналов следующим образом.

, (3.1)

где  - величина временного сдвига сигнала.

Формирование корреляционной функции в случае прямоугольного импульса показано на рис.3.1

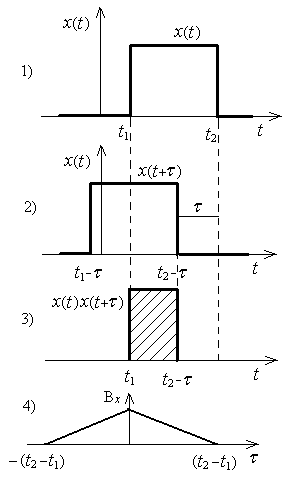
Рис.3.1

Ясно, что при =0 эта функция имеет максимум, величина которого равна энергии сигнала, т.е.

(3.2)

Эта функция четная, что легко доказать.

(3.3)

Для оценки степени связи между двумя различными сигналами x₁(t) и x₂(t) используется взаимная корреляционная функция, которая имеет следующий вид.

(3.4)

При =0 взаимная корреляционная функция не обязательно достигает максимума. Она не обязательно является четной функцией.

Существует особый случай, когда взаимная корреляционная функция двух гауссовых сигналов представляет собой гауссовую функцию. Пусть сигналы x₁(t) и x₂(t) определяются выражениями

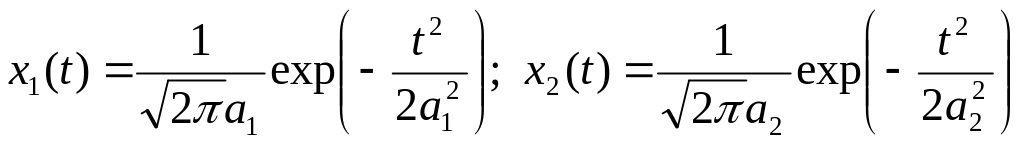(3.5)

Согласно формуле (3.4) можем записать взаимную корреляционную функцию так.

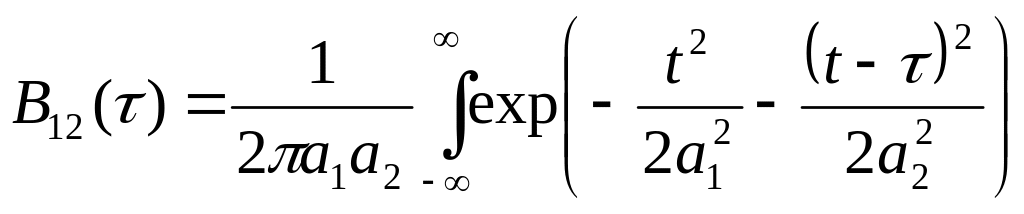(3.6)

Сделаем следующее преобразование

(3.7)

Второе слагаемое не зависит от переменной t. Соответствующая экспонента может быть вынесена за знак интеграла. Далее делаем замену переменной в виде

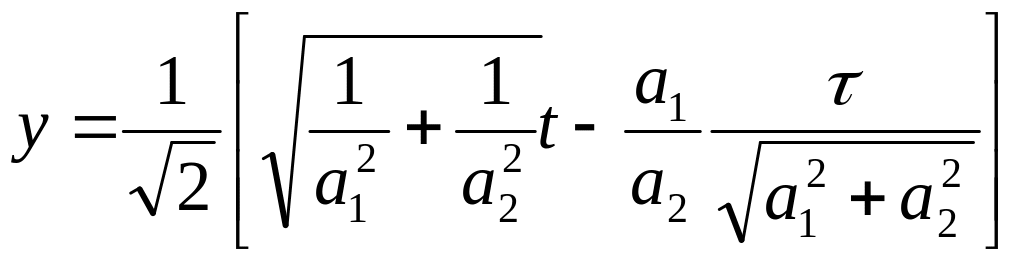
и учтем, что . В результате получим следующее выражение для взаимной корреляционной функции.

(3.8)

Таким образом, взаимная корреляционная функция двух гауссовых сигналов представляет собой гауссовую функция, причем параметр кривой а₁₂ функции однозначно связан с параметрами сигналов.

(3.9)

В случае периодического сигнала автокорреляционная функция вычисляется следующим образом.

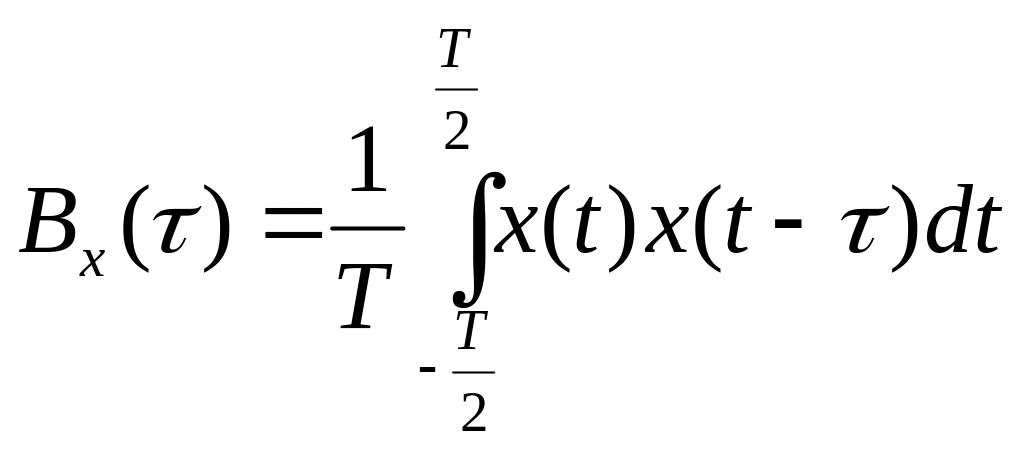(3.10)

где Т – период функции x(t).

Из этого определения следует, что автокорреляционная функция периодического сигнала также является периодической.

2) Найти асимптотическое поведение спектра энергии сигнала вида

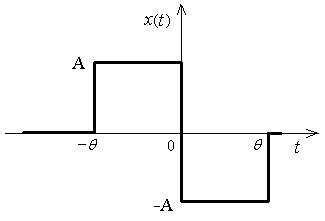
при больших частотах, не вычисляя его спектр. Какое значение имеет спектр на нулевой частоте.

Спектральную плотность энергии этого сигнала можно найти прямым вычислением спектральной плотности амплитуды и последующим вычислением квадрата ее модуля. Но проще воспользоваться другим подходом. Заметим, что интегрирование такого сигнала дает треугольный сигнал вида

(2.34)

Для треугольного сигнала (2.5) спектральная плотность энергии дается формулой (2.26). В этой формуле мы должны учесть, что амплитуда сигнала (2.34) имеет величину А вместо А для сигнала (2.5). Поэтому вместо (2.26) получаем спектральную плотность энергии сигнала (2.34) в виде

(2.35)

Теперь мы должны учесть, что сигнал, представленный на рис.2.13, получается путем дифференцирования треугольного сигнала (2.34). Следовательно, его спектральная плотность энергии получается умножением (2.35) на . В результате имеем, что

(2.36)

Этот спектр показан на рис.2.14. Значение спектральной плотности равно нулю на нулевой частоте.

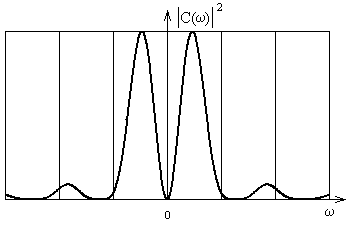
Рис.2.14

Асимптотика по максимумам равна

(2.37)

Коэффициент 16А² определяется тем, что в максимумах этого спектра скачки сигнала, представленного на рис.2.13, когерентно в фазе, независимо от знака скачка: (А+2А+А)=4А, что и приводит к (2.37).

Билет 9