Билет 1

1) Спектральная плотность амплитуды и спектр энергии действительного сигнала. Их основные свойства.

Сигнал первой группы может быть представлен в виде интеграла Фурье.

(2.8)

Функция является комплексной и называется спектральной плотностью амплитуды сигнала. Эта функция может быть вычислена с помощью обратного преобразования Фурье.

(2.9)

Поскольку сигнал является действительной функцией, из (2.9) нетрудно получить, что спектральная плотность амплитуды имеет следующее свойство симметрии , где звездочка сверху обозначает комплексное сопряжение.

Пусть в точку приема прибывают два одинаковых сигнала в два различные момента времени t=0 и t=. Тогда первый и второй сигналы могут быть представлены в единой системе координат, как и . Подставляя в уравнение (4), находим спектральную амплитуду второго сигнала в виде

(2.10)

Если в виде (2.8) подставить в (2.2), то получим энергию сигнала в виде

(2.11)

Функцию называют спектральной плотностью энергии сигнала или просто спектром энергии. В дальнейшем постоянный множитель будем не писать, а подразумевать и функцию также будем называть спектральной плотностью энергии. Так как , то она является четной функцией частоты, т.е. . Кроме того, спектральная плотность энергии является неотрицательной величиной, т.е. . Из (2.10) легко получить, что . Это значит, что спектральная плотность энергии не зависит от положения сигнала на оси времени (задержки сигнала).

Если мы будем применять анализатор спектра для измерения спектральной плотности энергии, то обнаружим, что он не может различить положительные и отрицательные частоты. Он измеряет суммарную величину спектральной плотности энергии, т.е. . В связи с этим будем называть функцию математической спектральной плотностью энергии, заданной на всей оси частот, а функцию - физической спектральной плотностью энергии, заданной только для положительных частот.

2) Канальная модель Кларка и спектр Джейкса.

Когда имеется много переотражателей, то естественно предположить, что они располагаются вокруг приемника равномерно, например, по окружности, как показано на рис. 2.17. Такая модель переотражателей называется моделью Кларка.

Рис. 2.17 Расположение переотражателей в моделе Кларка

Спектральная плотность мощности в случае модели Кларка определяется следующим путем. Выделим интервал частот df_d вблизи частоты f_d. Заключенная в этом интервале принимаемая мощность равна . Эта мощность обусловлена доплеровским смещением частоты (2.3.86). Рассеянная мощность, связанная с угловым интервалом d, равна , где - угловая плотность рассеянной мощности. Заметим, что одинаковое доплеровское смещение f_d наблюдается для переотражетелей с угловыми координатами  и (-). Отсюда вытекает следующее равенство мощностей

. (2.3.87)

Будем полагать, что полная рассеянная мощность равна единице и равномерно распределена в интервале [0-2) углов . Тогда (2.3.87) примет вид

. (2.3.88)

Отсюда находим спектральную плотность мощности

. (2.3.89)

Используя (2.3.85) для вычисления производной, получаем спектр (2.3.89) в виде

. (2.3.90)

Такой спектр называется доплеровским спектром Джейкса. Спектр Джейкса для максимальной частоты Доплера f_max=10 Гц показан на рис. 2.18. Его вид часто характеризуется, как «уши кролика». Этот спектр является четной функцией и заключен в интервале [-f_max, f_max].

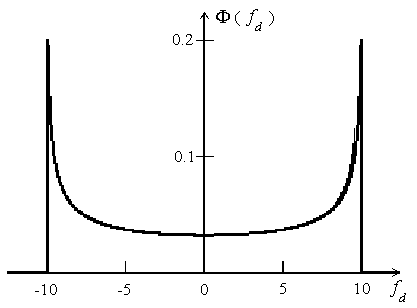
Рис. 2.18 Доплеровским спектр Джейкса для f_max=10 Гц