2) Вычислить спектральную плотность амплитуды и спектр энергии сигнала

Рассмотрим сигнал, представленный на рис.2.6.

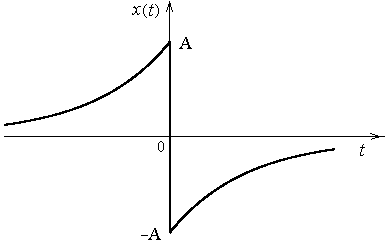
Рис.2.6

Используя (2.12) и (2.16), находим спектральную плотность амплитуды.

(2.17)

Отсюда находим спектральную плотность энергии в виде

(2.18)

Эта функция показана на рис.2.7.

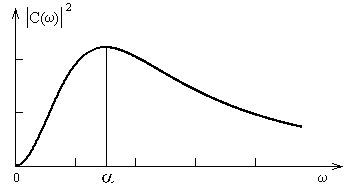
Рис.2.7

Поставим 3 вопроса. Почему этот спектр равен нулю на нулевой частоте? Почему в спектре имеется максимум на частоте =? Почему асимптотика спектра ( ) в 4 раза больше, чем для простого экспоненциального сигнала?

На первый вопрос мы находим ответ легко из формулы (2.9)

(2.19)

Билет 4

1) Случайные узкополосные сигналы. Релеевское распределение амплитуды и замирания сигнала в многолучевом канале связи.

Допустим, что величины I(t) и Q(t) в любой момент времени являются случайными, имеют нулевые средние значения и подчиняются нормальному закону распределения вероятностей, т.е.

(4.24)

Будем предполагать, что в совпадающие моменты времени величины I(t) и Q(t) являются статистически независимыми. Поэтому двумерную функцию плотности вероятности можно записать, как произведение одномерных функций распределения.

(4.25)

Теперь поставим задачу найти статистические свойства амплитуды А и фазы  нормального узкополосного процесса в некоторый фиксированный момент времени. Амплитуды А и фазы  связаны с квадратурными компонентами следующими соотношениями.

(4.26)

Геометрическая интерпретация параметров узкополосного сигнала ясна из Рис.4.6.

Рис.4.6

Вероятность попадания конца вектора А в темный прямоугольник малой площади равна . Поскольку существует однозначная связь (4.26) между квадратурными компонентами (I,Q) с одной стороны и амплитудой и фазой (А,) с другой стороны, то эту же вероятность можно записать в виде , где функция есть интересующая нас двумерная функция плотности вероятности параметров А и . Эти вероятности равны между собой, а двумерные функции плотности вероятности связаны между собой через якобиан преобразования координат следующим образом.

(4.27)

Чтобы найти якобиан преобразования, учтем, что . Тогда якобиан будет равен

(4.28)

Отсюда находим интересующую нас двумерную функцию плотности вероятности параметров А и .

(4.29)

Для определения одномерной функции плотности вероятности необходимо двумерную функцию плотности вероятности (4.29) проинтегрировать по всем возможным значениям фазы :

(4.30)

Распределение амплитуды (4.30) называется распределением Релея. Сигнал в таком канале испытывает замирания, так как его амплитуда может принимать малые значения.

Интегрируя двумерную функцию плотности вероятности (4.29) по всем возможным значениям амплитуды, находим функцию плотности вероятности следующим образом.

(4.31)

Используя замену переменной A²=z, находим

(4.32)

Отсюда следует, что фаза распределена равномерно в промежутке (0,2). Сопоставляя и с выражением (4.29) для , приходим к важному выводу, что

(4.33)

Это значит, что амплитуда и фаза нормального узкополосного процесса являются независимыми случайными процессами в совпадающие моменты времени.

Релеевское распределение амплитуды (4.30) для ²=2 показано на Рис.4.7.

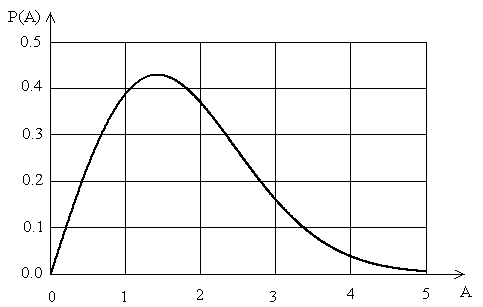
Рис.4.7

Релеевское распределение амплитуды зависит только от одного параметра . Максимум кривой находится в точке А=. Средняя величина амплитуды равна

(4.34)

Средняя мощность сигнала равна . Она делится между квадратурными компонентами поровну. Дисперсия амплитуды характеризует отклонение амплитуды от среднего значения и вычисляется по следующей формуле.

(4.35)

Медианное значение амплитуды показывает границу, ниже и выше которой амплитуда появляется с вероятностью 50%. Медианное значение амплитуды можно вычислить по формуле .

Если мы интересуемся вероятностью, с которой амплитуда А будет меньше заданной величины, то следует пользоваться интегральной функцией вероятности, которая имеет следующий вид.

(4.36)

Допустим, нас интересует вероятность того, что уровень сигнала опустится ниже медианного уровня на 10дБ и более. В этом случае пороговое значение амплитуды равно 10^-0,5А_m. Вероятность такого события равна примерно 7%.

Предположим теперь, что результирующий сигнал представляет собой сумму детерминированного и случайного релеевского сигналов. Геометрическая интерпретация суммирования этих сигналов показана на Рис.4.8.

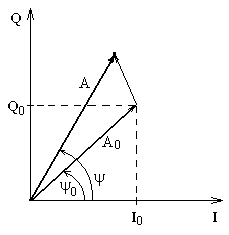
Рис.4.8

Здесь амплитуда и фаза для детерминированного сигнала обозначены как А₀ и ₀, а для суммарного сигнала как А и . Теперь вместо (4.24) одномерные функции распределения вероятностей квадратурных компонент необходимо записать в виде

(4.37)

Чтобы получить двумерную функцию распределения вероятностей , поступим аналогично рассмотренному выше случаю релеевских замираний. При этом в (4.27) сделаем замену: и и учтем якобиан преобразования координат А. В результате получим, что

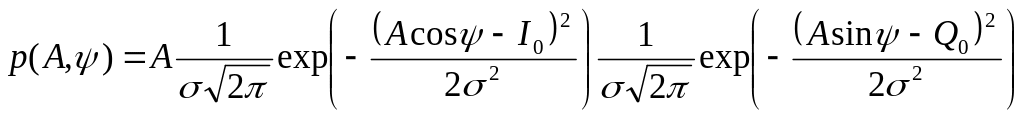(4.38)

Для определения одномерной функции плотности вероятности необходимо двумерную функцию плотности вероятности (4.38) проинтегрировать по всем возможным значениям фазы :

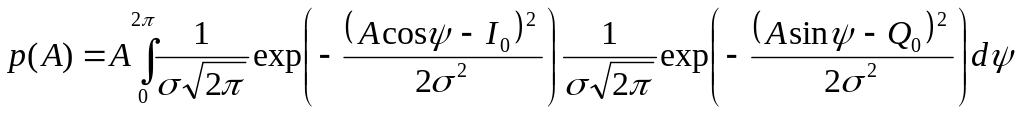(4.39)

После элементарных алгебраических преобразований это выражение принимает следующий вид.

(4.40)

Интеграл в этом выражении сводится к функции Бесселя нулевого порядка от мнимого аргумента I₀(x) путем замены . Также необходимо учесть, что для детерминированного сигнала . Таким образом, искомая функция распределения равна

(4.41)

Эта функция обобщает релеевский закон распределения (4.30), так как он следует из (4.41) в частном случае при А₀=0. Поэтому функция (4.41) носит название обобщенной функции распределения Релея. Ее называют также функцией распределения Райса или Релея-Райса. Несколько кривых распределения Райса для ²=2 показаны на Рис.4.9.

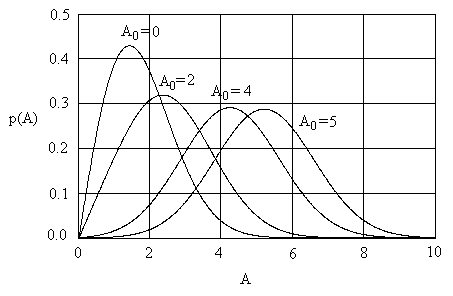
Рис.4.9

Распределения отличаются уровнем детерминированной компоненты А₀ в результирующем сигнале. Видно, что с увеличением детерминированной компоненты распределение плотности вероятности трансформируется и постепенно переходит от релеевского распределения (А₀=0) к нормальному распределению. Это можно подтвердить и математически. Если отношение А₀/σ велико, то в выражении (4.41) функцию Бесселя можно заменить ее асимптотическим разложением

(4.42)

Тогда формула (4.41) преобразуется к виду

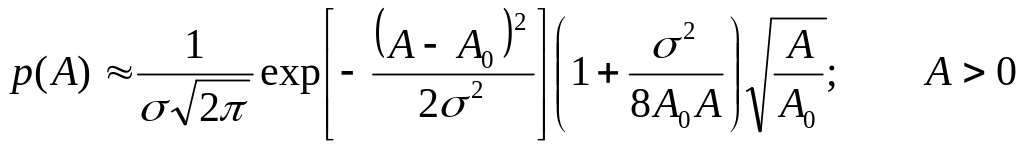(4.43)

Отсюда видно, что, если множитель близок к единице, распределение (4.43) близко к нормальному с параметрами А₀ и σ.

Когда отношение А₀/σ мало, то обобщенная функция Релея мало отличается от (4.30), причем поправка может быть получена путем разложения функции Бесселя в степенной ряд. Ограничиваясь только первыми двумя членами этого разложения, получаем

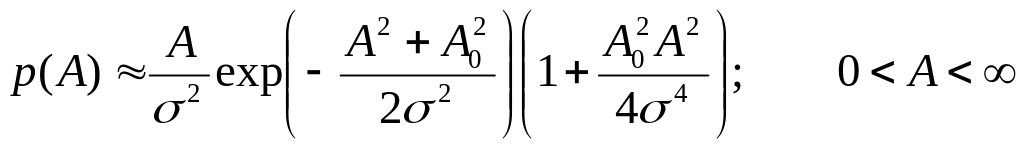(4.44)