Билет 2

1) Три способа представления узкополосного сигнала. Принцип работы модулятора и демодулятора.

Подавляющее большинство систем радиосвязи работают, используя узкополосные сигналы. В отличие от гармонического сигнала с фиксированными амплитудой и начальной фазой, амплитуда и фаза узкополосного сигнала являются медленно меняющимися функциями. Такой сигнал запишем в виде

(4.1)

Такой сигнал можно представить другим способом, если воспользоваться известной тригонометрической формулой

(4.2)

Эта формула дает разложение узкополосного сигнала на два ортогональных сигнала: и . Поскольку косинусное и синусное колебания сдвинуты по фазе на 90, говорят, что эти колебания происходят в квадратуре. Соответственно, формула (4.2) называется квадратурным разложением узкополосного сигнала. В иностранной литературе формулу (4.2) принято называть (I,Q)-разложением и записывать в виде

(4.3)

где .

Квадратурное разложение узкополосного сигнала широко используется в системах связи для построения модуляторов. Принцип работы модулятора изображен на рис.4.1.

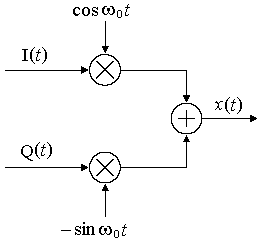
Рис.4.1

При приеме узкополосного сигнала его разложение на две квадратуры выполняется, используя ортогональность косинусного и синусного колебаний. Соответствующие формулы преобразования имеют вид.

(4.4)

(4.5)

Схема обработки сигнала с целью выделения отдельных квадратур показана на рис.4.2.

Рис.4.2

Наконец, существует третье представление узкополосного сигнала, которое математически можно записать так.

(4.6)

Величина носит название комплексной амплитуды узкополосного сигнала. Ее можно записать также в виде . Отсюда следует, что .

2) Вычислить спектральную плотность амплитуды и спектр энергии сигнала

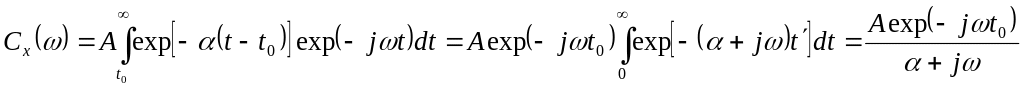(2.12)

Отсюда находим спектральную плотность энергии в виде

(2.13)

График этой функции показан на рис.2.4. Спектральная плотность энергии не зависит от знака амплитуды и начального момента импульса t₀. Спектральная плотность энергии определяет исходный сигнал неоднозначно.

Рис.2.4

Как определить полосу спектра сигнала? Можно найти частоту, где спектр спадает вдвое. Однако гораздо удобнее иметь дело с энергетической полосой, которая определяется шириной прямоугольника, равновеликого по площади половине энергии сигнала.

. Для спектра (2.13) получим, что . Учитывая, что длительность сигнала равна , находим, что

(2.14)

Формула (2.14) говорит о том, что сигнал, меньшей длительности имеет более широкий спектр, причем ширина спектра обратно пропорциональна длительности сигнала. Коэффициент пропорциональности зависит от формы сигнала.

Билет 3

1) Комплексная амплитуда узкополосного сигнала. Рассмотреть пример вычисления комплексных амплитуд сигналов для антенной решетки в случае приема плоской волны.

Комплексная амплитуда играет важную роль при анализе и синтезе линейных устройств типа фильтров или антенных решеток.

Допустим, что узкополосный сигнал на приемном конце линии связи принимается несколькими антеннами. Множество принятых сигналов затем суммируются. При этом амплитуда и фаза каждого сигнала подвергаются изменениям в соответствие с некоторым заданным алгоритмом обработки сигнала. Таким образом, мы можем написать, что результирующий сигнал равен

(4.7)

Теперь воспользуемся представлением узкополосного сигнала (4.6) и вместо (4.7) получим следующий результат.

(4.8)

где – комплексные весовые коэффициенты.

Мы видим, что такая обработка сигнала сводится только к изменению комплексной амплитуды сигнала. Результирующая комплексная амплитуда сигнала равна взвешенной сумме отдельных комплексных амплитуд.

(4.9)

Прием гармонического сигнала с помощью антенной решетки.

Предположим, что N элементов эквидистантной АР распределены вдоль оси x, как это показано на рис.4.3. Начало координат выбрано в точке расположения крайнего левого элемента решетки с номером 1. Межэлементное расстояние обозначено буквой d.

Рис.4.3

Предположим, что плоская монохроматическая волна единичной амплитуды падает на АР под углом φ по отношению к оси y. Волна возбуждает гармоническое электрическое колебание в каждом элементе АР. Без ограничения общности начало отсчета времени можно выбрать так, что при t=0 фаза колебания равна нулю в первом элементе решетки.

Таким образом, сигнал, принятый первым элементом, можно представить в виде

, (4.10)

где j - мнимая единица; - циклическая частота; - частота колебания, Гц.

Комплексная амплитуда этого сигнала просто равна единице.

Колебание во втором элементе АР опережает колебание в первом на время , которое легко определить, используя рис.4.3. Из геометрических соображений находим, что

, (4.11)

где с - скорость распространения электромагнитных волн, которую мы считаем равной скорости света, так как не рассматриваем влияние среды.

За время  фаза колебания второго элемента АР увеличивается на величину по отношению к фазе колебания в первом элементе. Поэтому сигнал, принятый вторым элементом, можно записать как

. (4.12)

Подставляя (4.11) в (4.12) и учитывая, что длина волны =с/f₀, находим колебание, возбуждаемое волной во втором элементе, в виде

. (4.13)

Здесь первый множитель дает комплексную амплитуду сигнала во втором элементе.

Выражение (4.13) легко получить также, применяя в качестве исходной формулу, описывающую распространение плоской волны,

, (4.14)

где - волновое число; r – расстояние, пробегаемое волной.

Из рис.4.3 видно, что расстояние, которое волна проходит до второго элемента меньше, чем расстояние, которое она проходит до первого элемента, на величину . Эта разница в расстояниях называется обычно разностью хода волны. Разность фаз колебаний, получающаяся из-за разности хода, определяется умножением разности хода на волновое число, как показывает формула (1.5). Таким образом, мы находим, что разность фаз равна , что соответствует выражению (4.14).

Теперь легко понять, что колебания, возбуждаемые волной в разных элементах АР, отличаются только разностью фаз _n, которая зависит от номера элемента n следующим образом:

. (4.15)

Обобщая (4.13), с помощью (4.15) получим выражение, описывающее колебания во всех элементах АР:

. (4.16)

Второй множитель в этом выражении зависит только от частоты колебания. Он одинаков для всех элементов АР, поэтому не несет информации о геометрии АР и направлении прихода волны. Во многих задачах этот множитель опускают из рассмотрения. Первый множитель называют комплексной амплитудой сигнала. Именно он имеет существенное значение в задачах, связанных с обработкой сигнала. Обозначим комплексную амплитуду как S_n. Тогда выражение (4.16) принимает вид

. (4.17)

Антенная решетка представляет собой многоканальную систему, так как волна возбуждает одновременно N колебаний различной амплитуды. Математика дает нам возможность описать единообразно всю совокупность сигналов (4.17), если ввести вектор комплексных амплитуд S и вектор сигналов s(t), следующим образом: