2) Каким образом связаны между собой функция автокорреляции действительного сигнала и его спектр энергии ?

Корреляционная (или автокорреляционная) функция сигнала определяется для детерминированных вещественных сигналов следующим образом.

,

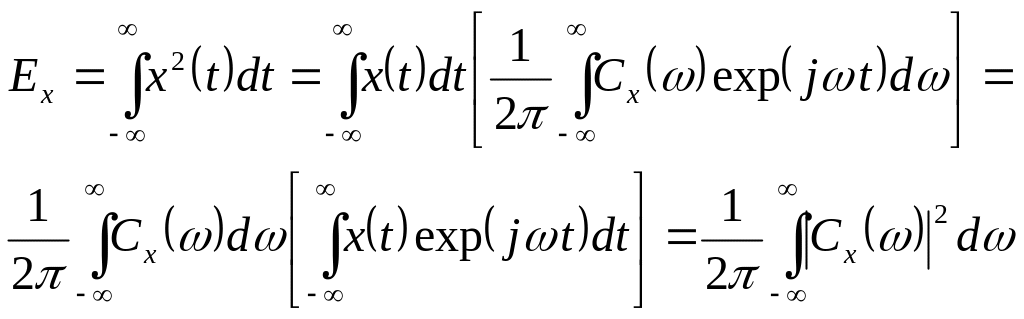
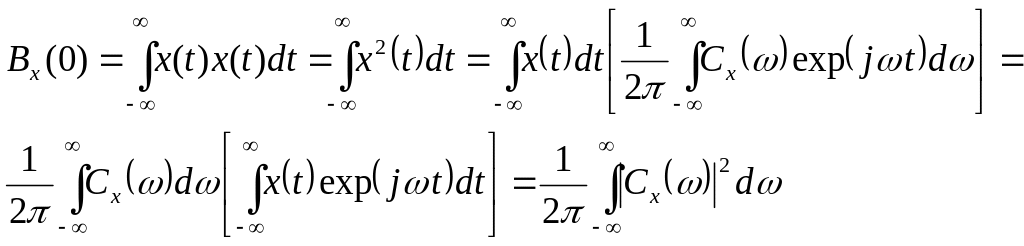
Билет 23

1) Оценка импульсной характеристики многолучевого канала при известной длине импульсной характеристики.

рассмотрим более общую задачу, когда ИХ содержит (m+1) канальных коэффициентов h(0), h(1),..., h(m) и для канального оценивания применяется последовательность сигналов длительностью L. В этом случае приемник регистрирует последовательность сигналов

. (8.1.18)

Плотность вероятности входного сигнала x(k) будет иметь следующий вид:

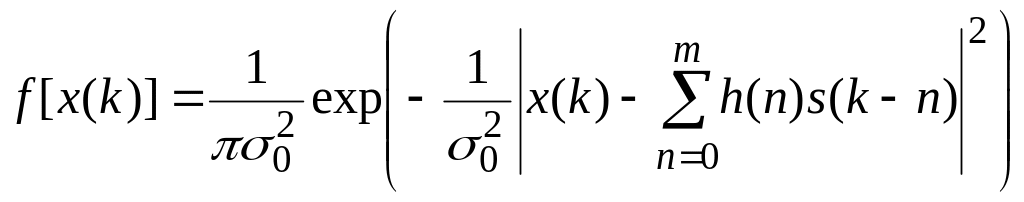. (8.1.19)

Поскольку имеет место задержка сигналов в канале, для оценки канальных коэффициентов необходимо увеличить длину последовательности принятых сигналов по сравнению с длиной L обучающей последовательности. В данном случае число задержанных сигналов равно m, и поэтому длину последовательности принятых сигналов выберем равной L+m.

Принятые сигналы x(1), x(2),..., x(L+m) являются статистически независимыми. Поэтому их совместная плотность вероятности равна произведения одномерных функций плотности вероятности (8.1.19) и, следовательно, мы можем записать, что

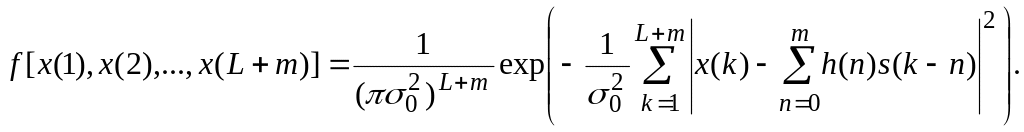(8.1.20)

В общем случае неизвестными величинами в (8.1.20) являются значения ИХ h(0), h(1),..., h(m) и число задержанных лучей m. Однако сейчас мы предполагаем, что число задержанных лучей m задано. Мощность собственного шума обычно считается известной, поскольку может быть измерена. Однако для общности рассмотрения будем предполагать, что мощность собственного шума также подлежит оценке, как параметр функции правдоподобия (8.1.20). Значения искомых параметров, которые обеспечивают максимальное значение функции правдоподобия (8.1.20), называются максимально правдоподобными оценками этих параметров.

Найдем логарифм от функции правдоподобия (8.1.20) в виде

. (8.1.21)

Максимум плотности вероятности будет иметь место при выполнении следующих условий:

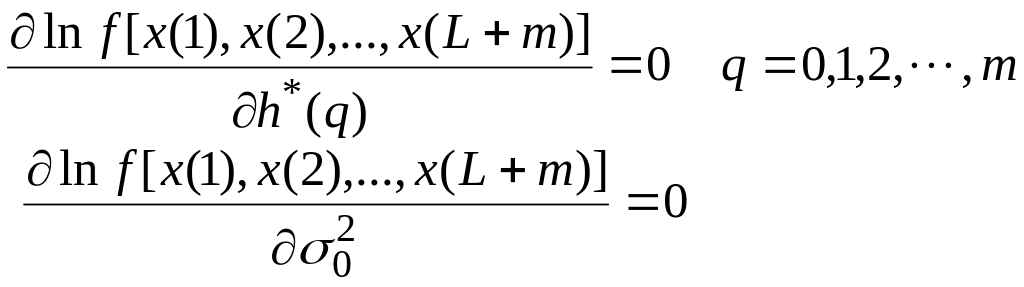. (8.1.22)

По сути, первые (m+1) условий в (8.1.22) представляют собой (m+1) линейных уравнений, из которых можно найти оценки канальных коэффициентов h(0), h(1),..., h(m). Эти уравнения имеют вид

. (8.1.23)

Для удобства дальнейшего анализа введем в рассмотрение матрицу M и вектор R с элементами

, , (8.1.24)

и перепишем (8.1.23) в виде

, (q=0,1,2,..., m). (8.1.25)

Второе условие в (8.1.22) дает нам оценку дисперсии шума в виде

. (8.1.26)

Если канальные оценки , полученные путем решения системы уравнений (8.1.25), подставить в (8.1.26), то мы получим оценку дисперсии шума .

Если не делать предположения о гауссовости шума z(k), то уравнение (8.1.26) может быть рассмотрено как квадратичный функционал от переменных h(0), h(1),..., h(m). Минимизируя этот функционал, мы придем к (8.1.25). Таким образом, в случае гауссовского шума обе оценки (наименьшей квадратичной ошибки и максимального правдоподобия) будут давать одинаковый результат.

Решение задачи представим более компактно в векторно-матричной форме. Введем векторы входных данных , шумов , ИХ и обучающих сигналов S₀, S₁, S₂, …, S_m размерности (L+m) и равных

(8.1.27)

Векторы S₀, S₁, S₂, …, S_m будем называть обучающими векторами. Они отличаются друг от друга тем, что обучающая последовательность сдвигается на одну позицию при смене индекса обучающего вектора на единицу. Объединим обучающие векторы в матрицу S следующим образом.

. (8.1.28)

Теперь уравнение (5.1.18) в векторно-матричной форме можно записать так:

. (8.1.29)

Многомерную функцию плотности вероятности (8.1.20) теперь запишем следующим образом

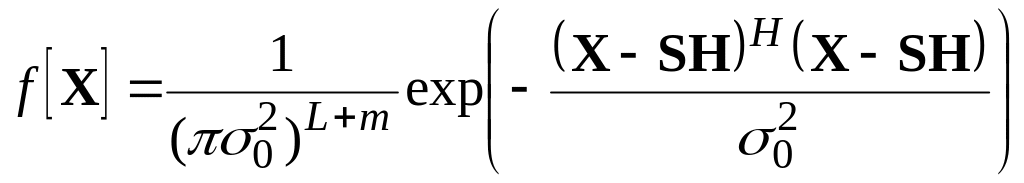. (8.1.30)

Уравнения (8.1.25) и (8.1.26) также могут быть записаны в векторно-матричной форме.

, (8.1.31)

. (8.1.32)

Введенные ранее матрица M и вектор R теперь запишем следующим образом: M=S^HS и вектор R=S^HX.

Матрица M является эрмитовой и представляет собой матрицу Грамма, составленную из скалярных произведений обучающих векторов S₀, S₁, S₂, …, S_m:

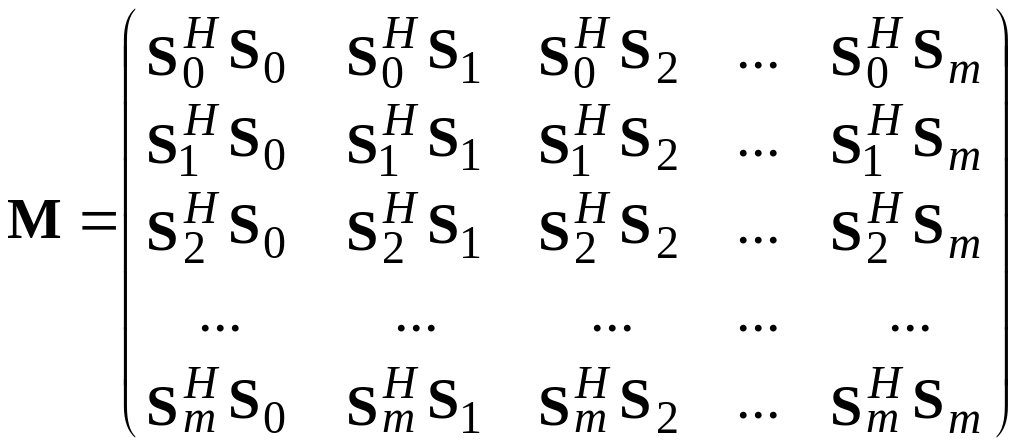. (8.1.33)

Элементами главной диагонали матрицы M являются квадраты модулей обучающих векторов. Будем предполагать, что сигналы обучающей последовательности имеют одинаковые амплитуды s. Тогда диагональные элементы M(n,n) равны между собой:

. (8.1.34)

Компоненты вектора R являются скалярными произведениями обучающих векторов S_n и вектора X входных сигналов.

Решение уравнения (8.1.31) дает оценку ИХ в виде

. (8.1.35)

Подставим сюда вектор принятых сигналов (8.1.29) и найдем, что

. (8.1.36)

Ясно, что оценка является случайной величиной и, строго говоря, не совпадает с точным значением ИХ H. Среднее значение оценки равно . Это значит, что оценка является несмещенной.

Точность оценивания определяется матрицей ошибок, которая по определению равна

. (8.1.37)

Используя (8.1.36), преобразуем это выражение к виду

. (8.1.38)

Учтем, что корреляционная матрица шума <ZZ^H>=₀²I. Тогда

. (8.1.39)

Допустим, что обучающие векторы являются ортогональными, а сигнала имеют одинаковую амплитуду. Тогда матрица M имеет диагональный вид с элементами (8.1.34). В этом случае матрица ошибок канального оценивания  также является диагональной и имеет одинаковые элементы равные

. (8.1.40)

В этом случае оценки отсчетов ИХ h(n) (n=0,1,2, ..., m) будут статистически независимы между собой, а точность их оценивания будет одинаковой.

В общем случае точность оценки (8.1.36) определяется следующими факторами:

• ОСШ для сигналов обучающей последовательности. Увеличение ОСШ увеличивает точность оценивания ИХ;

• длина обучающей последовательности. Ее увеличение ведет к уменьшению ошибки;

• степень ортогональности обучающих векторов S₀, S₁, S₂, …, S_m.

Требование ортогональности обучающих векторов имеет важное значение. Если обучающая последовательность выбрана неудачно (нет ортогональности обучающих векторов), то матрица М становится близкой к сингулярной матрице, а некоторые ее собственные числа становятся близкими к нулю. Это приводит к уменьшению точности оценивания, так как согласно (8.1.39) матрица ошибок определяется обратной матрицей M^1, собственные числа которой возрастают. Чтобы обеспечить хорошую точность оценивания ИХ, необходимо выбрать обучающие последовательности таким образом, чтобы базис, построенный на соответствующих векторах, был бы максимально близок к ортогональному. Для этого детерминант матрицы M должен быть близок к максимальному значению, равному (det(M))_max=L^m+1 при единичной амплитуде сигнала.

Рассмотрим два примера генерирования двоичной обучающей последовательности длительностью 26 символов, каждый из которых может принимать только два значения 1 или -1. Первые 5 сигналов последовательности назначаются произвольно, а последующие сигналы определяются с использованием следующих соотношений: s(k)=-s(k-5)s(k-3) (пример 1) и s(k)=-s(k-5)s(k-2) (пример 2). Таким образам, в каждом из примеров мы можем получить 32 (2⁵) последовательности сигналов, которые могут рассматриваться в качестве обучающих. Для каждой такой последовательности вычислим det(M) и найдем его отношение к максимально возможному значению равному L^m+1. В таблице 8.1 представлены результаты расчетов этого отношения для всех возможных последовательностей.

Таблица 8.1.

Номер	Начальные комбинации сигналов	Пример 1	Пример 2
1	11111	0,9679	0,9733
2	1111-1	0,9419	0,9671
3	111-11	0,9303	0,9130
4	111-1-1	0,9009	0,0000
5	11-111	0,9375	0,0000
6	11-11-1	0,8746	0,0000
7	11-1-11	0,9216	0,8032
8	11-1-1-1	0,9446	0,0000
9	1-1111	0,9671	0,8432
10	1-111-1	0,8032	0,8543
11	1-11-11	0,0000	0,9465
12	1-11-1-1	0,9465	0,9432
13	1-1-111	0,8635	0,8032
14	1-1-11-1	0,9130	0,0000
15	1-1-1-11	0,8543	0,0000
16	1-1-1-1-1	0,0000	0,8635
17	-11111	0,0000	0,9303
18	-1111-1	0,9733	0,8175
19	-111-11	0,9432	0,8532
20	-111-1-1	0,8032	0,9446
21	-11-111	0,0000	0,9441
22	-11-11-1	0,0000	0,8746
23	-11-1-11	0,0000	0,9679
24	-11-1-1-1	0,8432	0,8828
25	-1-1111	0,0000	0,9375
26	-1-111-1	0,8828	0,0000
27	-1-11-11	0,9196	0,0000
28	-1-11-1-1	0,8175	0,9419
29	-1-1-111	0,9441	0,9196
30	-1-1-11-1	0,0000	0,9009
31	-1-1-1-11	0,8532	0,9216
32	-1-1-1-1-1	0,0000	0,0000

Для определения «лучшей» обучающей последовательности (в смысле ортогональности обучающих векторов) в таблице 8.1 нужно найти значения, близкие к единице. Нулевые значения соответствуют обучающим последовательностям, которые не подходят для оценивания ИХ, так как они образуют линейно зависимые системы обучающих векторов. Видно, что лучшими последовательностями являются последовательности №1, 9 и 18 (в примере 1) и № 1, 2 и 23, (в примере 2), а худшими - № 11, 16, 17, 21, 22, 23, 25 (в примере 1) и № 4, 5, 6, 14, 15, 26, 27 (в примере 2).

Для выяснения смысла оценки (8.1.35) введем систему так называемых взаимных векторов [51]. Эти векторы являются взаимными по отношению к обучающим векторам. Матрица взаимных векторов имеет вид

. (8.1.41)

Тогда оценка ИХ (8.1.35) будет равна

. (8.1.42)

Отсюда ясно, что процедура оценивания ИХ канала сводится к проектированию вектора X принятых сигналов на систему взаимных векторов. Каждая проекция вектора X дает оценку одного канального коэффициента. На практике взаимные векторы могут быть подготовлены заранее и храниться в памяти вычислителя. Поэтому для оценки ИХ канала требуется mL комплексных умножений и столько же сложений.

Взаимные векторы не являются ортогональными, так как матрица Грамма не диагональная. В тоже время . Это значит, что взаимный вектор с индексом k является ортогональным всем обучающим векторам, кроме вектора с индексом k. Благодаря этому возможно независимое оценивание канальных коэффициентов.

Входящие в (8.1.29) векторы принятых сигналов X и шума Z принадлежат пространству размерности L+m. В тоже время обучающие векторы сосредоточены в подпространстве размерности (m+1). Вектор шума Z может быть представлен в виде суммы ортогональных векторов _col и _ort. Вектор _col находится в (m+1)-мерном подпространстве обучающих векторов (8.1.33), а вектор _ort принадлежит ортогональному подпространству размерности (L-1). Так как собственный шум является однородным, то его средняя мощность в подпространстве обучающих векторов равна (m+1)₀² и в оставшемся подпространстве - (L-1)₀². Следовательно, минимальное значение выражения (8.1.32) полностью определяется значением мощности шума в ортогональном подпространстве и равно

. (8.1.43)

Среднее значение мощности этого шума равно

. (8.1.44)

Шум из ортогонального подпространства не влияет на точность оценки ИХ, которая определяется только шумовой компонентой _col.