2) Найти функцию автокорреляции прямоугольного сигнала, длительность и амплитуда которого равны т и а соответственно.

, (3.1)

где  - величина временного сдвига сигнала.

Формирование корреляционной функции в случае прямоугольного импульса показано на рис.3.1

Рис.3.1

Ясно, что при =0 эта функция имеет максимум, величина которого равна энергии сигнала, т.е.

(3.2)

Эта функция четная, что легко доказать.

Билет 15

1) Фазовая модуляция, используемая в системах цифровой связи.

При цифровой фазовой модуляции M сигналов на интервале времени (0 t T) можно представить в виде

(5.10)

где g(t) - огибающая сигнала, а определяет M возможных значений фазы несущей, которая переносит передаваемую информацию. Цифровую фазовую модуляцию (ФМ) называют также модуляцией с фазовым сдвигом.

Заметим, что рассматриваемые сигналы имеют одинаковую энергию, т.е.

(5.11)

ФМ сигналы являются двумерными сигналами. Поэтому их можно представить как линейную комбинацию двух ортонормированных сигналов f₁(t) и f₂(t), т.е.

, (5.12)

где

(5.13)

Обозначим двумерный вектор с компонентами

(5.14)

Пространственные диаграммы ФМ сигналов для М=2,4 и 8 даны на рис. 5.2. Видно, что случаю М=2 соответствуют одномерные противоположные сигналы, которые идентичны рассмотренным ранее двоичным сигналам АМ.

Рис. 5.2.

Евклидово расстояние между точками ФМ сигналов равно:

(5.15)

Минимальное расстояние по Евклиду соответствует случаю, когда ,

(5.16)

2) Найти функцию автокорреляции гармонического сигнала .

Найдем автокорреляционную функцию гармонического сигнала . Применяя (3.10), получим, что

(3.11)

Первый интеграл равен T/2, а второй – нулю. Таким образом, окончательно получаем

(3.12)

При =0 , т.е. есть средняя за период мощность гармонического сигнала, амплитуда которого равна А. Автокорреляционная функция гармонического сигнала не дает никакой информации о фазе сигнала.

Билет 16

1) Квадратурная амплитудная модуляция, используемая в системах цифровой связи.

Одновременная передача двух отдельных k-битовых информационных блоков на двух несущих, находящихся в квадратуре (cos2f_ct и sin2f_ct), называется квадратурной АМ или КАМ (QAM). Соответствующие сигналы на интервале времени (0 t T) можно выразить так:

(5.17)

где A_mc и A_ms – информационные амплитуды сигнала для квадратурных несущих, а g(t) – форма импульса.

Сигнал КАМ можно записать также в виде

(5.18)

где и .

Из этой формулы видно, что сигнал КАМ можно рассматривать как комбинацию амплитудной и фазовой модуляций. Мы можем образовать определенную комбинацию М₁-уровневой АМ и М₂-позиционной ФМ. В результате получается сигнальное созвездие комбинированной АМ-ФМ, содержащее М=М₁М₂ точек пространства сигналов. Если М₁=2ⁿ и М₂=2^m, то сигнальное созвездие позволяет передавать m+n=logM₁M₂ двоичных символов, возникающих со скоростью R/(m+n). Для M=8 и M=16 пространственные диаграммы сигналов представлены на рис. 5.3.

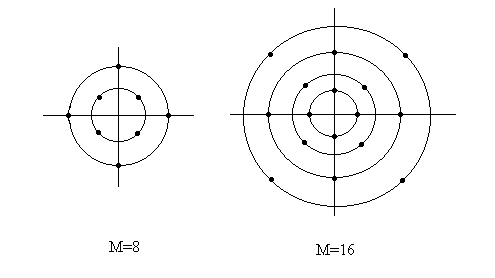
Рис. 5.3

КАМ сигналы являются двумерными сигналами. Поэтому их можно представить как линейную комбинацию двух ортонормированных сигналов f₁(t) и f₂(t), т.е.

(5.19)

где

(5.20)

и

(5.21)

Расстояние Евклида между произвольной парой сигнальных векторов равно

(5.22)

Для частного случая, когда амплитуды квадратурных сигналов принимают дискретные значения , пространственная диаграмма является прямоугольной, как показано на рис. 5.4.

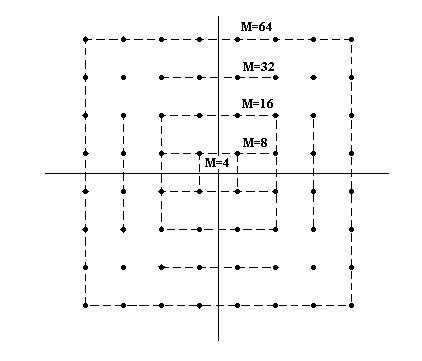
Рис. 5.4

В этом случае минимальное расстояние между сигналами равно

(5.23)

Такой же результат мы имели для АМ сигналов.