4.2. Экстраполяция и оценка погрешности при известном порядке аппроксимации.

В качестве исходного положения будем считать, что известно некоторое число членов последовательности z_n.

Например, оценка по правилу Рунге основана на предположении, что известен порядок точности численного метода (или порядок аппроксимации), т.е. z_nможно представить в виде

, (2.4)

где z– точное значение;z_n– приближенный результат, полученный при числе узловых точек (или числе слагаемых суммы) равномn;c₁– коэффициент, который предполагается не зависящим отn;k–порядок точности метода (или порядок аппроксимации);(n) – величина, полагаемая малой по сравнению сc₁n^-kпри тех значенияхn, которые использовались в данных конкретных расчетах.¹

Правила Рунге и Ричардсона. Одним из наиболее распространенных способов оценки погрешности численных методов с помощью экстраполяции, является правило Рунге [1].

В этом случае, уменьшив nвQраз (предполагается, чтоQ>1 иn/Q- целое), отбросив малые, приходим к системе двух уравнений

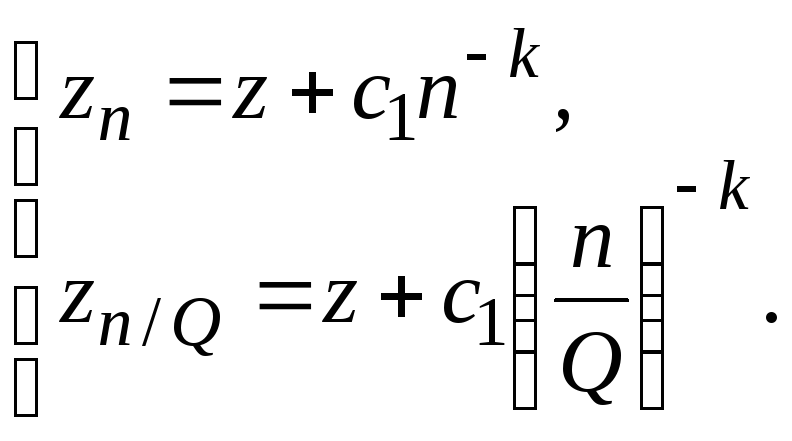(2.5)

Вычитая первое уравнение из второго, найдем

,

откуда нетрудно найти c₁, а, тем самым иz:

, (2.6)

С помощью (2.6) определяется экстраполированное (по правилу Ричардсона) значение искомого параметраz, а с его помощью оценивается погрешностьz_n‑zприближенного значения z_n. Этот способ оценки погрешности называетсяправилом Рунге.

Метод Ромберга. В некоторых случаях можно построить более подробную математическую модель погрешности, представив приближенный результат в виде суммы

. (2.7)

Тогда, чтобы найти неизвестные z,c₁,…,c_Lнужно использоватьL+1 значениеz_iи записать задачу в виде системы линейных уравнений, пренебрегая малыми величинами:

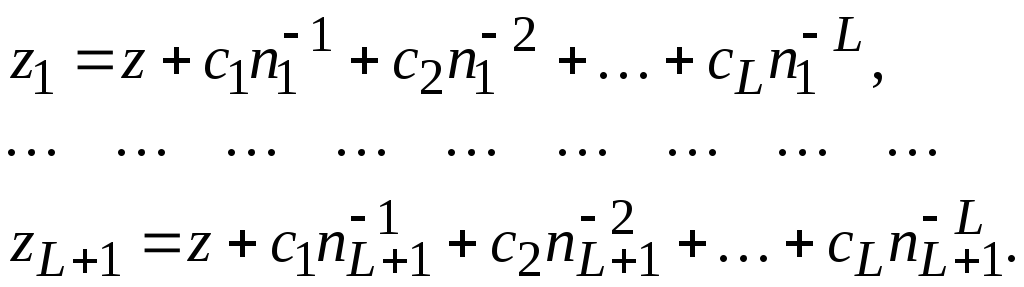(2.8)

Эта задачу можно решить путем построения интерполяционного многочлена Лагранжа [1,2] L-й степени

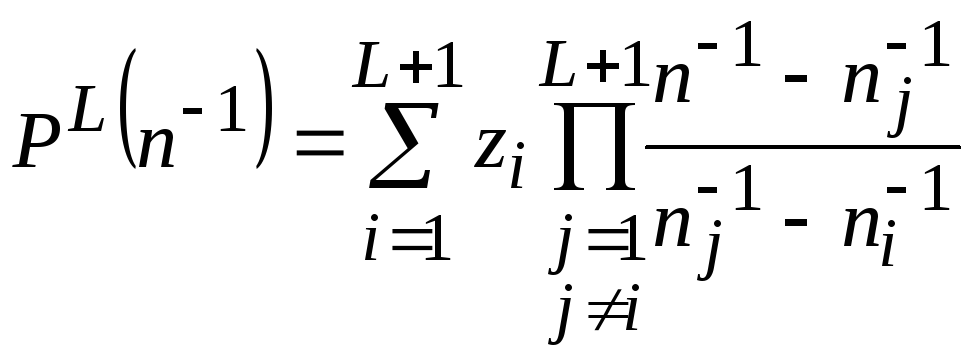
и экстраполяцией его до n

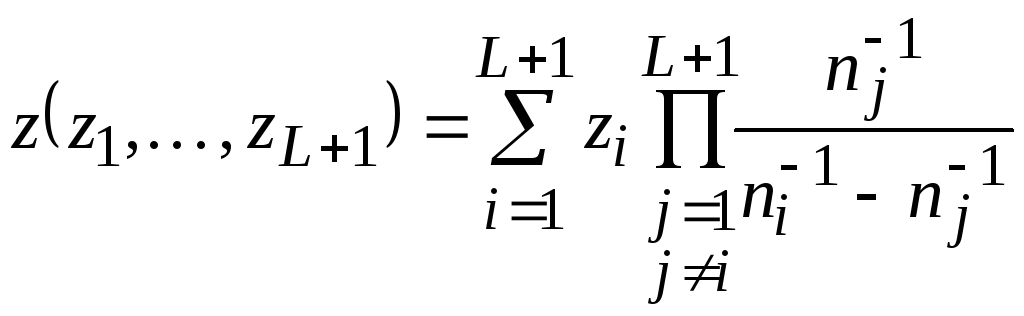(2.9)

(в скобках перечислены числа z_i, которые использованы для получения экстраполированного значенияz).

Интерполяционная формула обладает весьма полезным для практического применения свойством. Значение z, которое получается по формуле (2.9), может быть найдено путем последовательного применения рекуррентного соотношения Эйткена

, (2.10)

то есть для получения экстраполированного значения L+1-го порядка можно использовать два значенияL-го порядка, вычисленные для двух наборов данныхz_i, причем номер первой точки одного набора сдвинут на единицу относительно другого.

В случае если n_j=n₁Q^j1, выражение (2.10) принимает вид

, (2.11)

что при L=1 совпадает с (2.6), а приL>1 представляет собой аналогичное выражение, в котором вместо вычисленных участвуют экстраполиро­ванные значения.

Повторное применение правила Рунге для оценки погрешности результата вычислений z_nпри последовательном увеличении номераnвQраз называютметодом Ромберга [1].

Аналогичный подход имеет место и в случае, когда номер члена последовательности увеличивается на единицу (т.е. n_j+1=n_j+1). Для последовательности {z_n} строитсятаблица Нэвилла [7,8], представляющая собой матрицуz_jL(, ), в которой нулевой столбец – исходная последовательность, а все остальные столбцы находятся по правилу

. (2.12)

В более общем случае приближенный результат представляется в виде

, (2.13)

где k₁,…, k_L– произвольные действительные числа. Тем не менее, приn_j=n₁Q^j1задача определения коэффициентовc_iи экстраполированного значенияzрешается аналитически. Подставив в (2.8)n_j=n₁Q^j1преобразуем систему уравнений:

Введя обозначения , получим

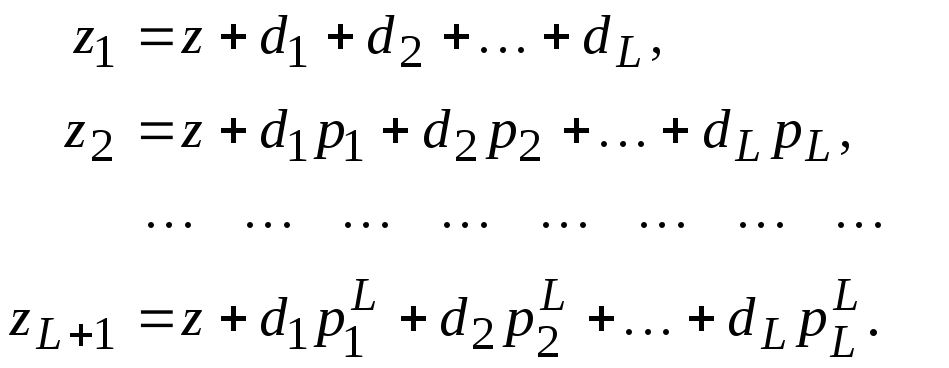(2.14)

Вычитая в (2.14) предыдущее уравнение, умноженное на p₁, из последующего, будем иметь

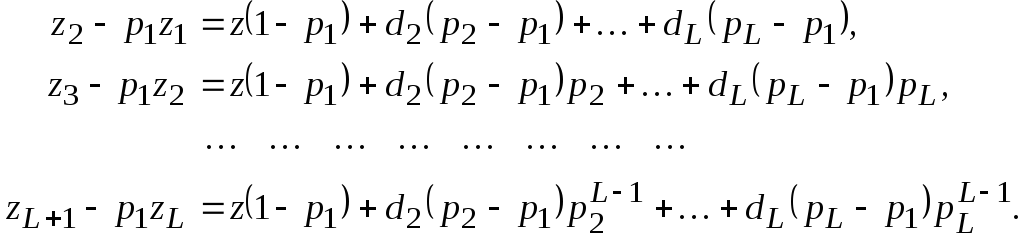
Разделив все уравнения на 1p₁и обозначив,, приходим к новой системе

(2.15)

которая по виду аналогична (2.14), но имеет на одно неизвестное меньше. Повторяя этот процесс Lраз, можно найтиz. Отметим, чтопредставляют собой Ричардсоновские экстраполяции (2.6).

Таким образом, определение искомого значения zи в случае произвольных (в общем случае не целых) показателяхk_i(но только приn_j=n₁Q^j1) сводится к повторному использованию уточнения (2.6), то есть, к методу Ромберга.

В случае n_jn₁Q^j1задача экстраполяции сводится к решению системыL+1 линейных уравнений типа (2.13) численным методом.

Главным ограничением для применения рассмотренных методов, основанных на разложении по степеням n, является то, что показатели степенейk_jдолжны быть известны заранее.