4.2. -Алгоритм
-алгоритмсостоит в построении
треугольной матрицы
,
в которой первые 2 столбца задаются по
правилу
,
далее
.
(3.6)
Тогда числа
представляют собой значенияz,
полученные из точного решения системы
2j+1 нелинейных уравнений
типа (2.14), в которой неизвестными являются
и коэффициентыdiи числа
.
Элементы нечетных столбцов
содержат решения аналогичных систем,
в которых используются значенияzlдляl=i-2j,…,i.
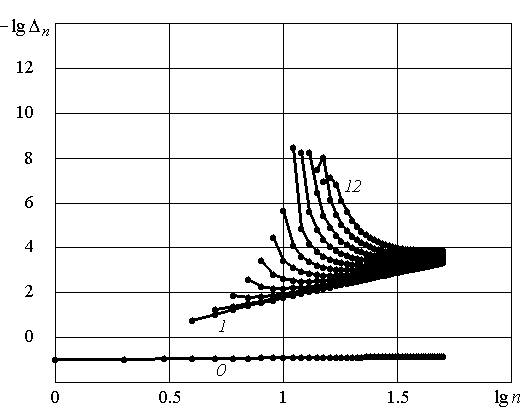
Результаты применения -алгоритма для экстраполяции последовательности сумм (2.2) даны на рис. 3.2а. Номера прямыхj=0,1,… соответствуют 2j+1 столбцам-матрицы.
|
а) |
б) |
Рис. 3.2. Результаты экстраполяции с помощью -алгоритма:
а) – последовательности сумм (2.2); б) – упрощенной последовательности (3.5).
Сравнивая рис. 3.2а с 3.1а нетрудно обнаружить заметное улучшение точности экстраполяции при применении -алгоритма, особенно, для трех и более раз экстраполированных данных. Это является следствием точного решения системы уравнений (2.14). Тем не менее, метод Ромберга дает лучшие результаты (рис. 3.2а), так как использует известные значения показателейkj, и поэтому допускает меньшую ошибку экстраполяции.
Точность решения системы уравнений иллюстрируется на рис. 3.2б, где показаны результаты применения -алгоритма к упрощенной последовательности (3.5). Погрешность порядка 10131014, которая остается после применения трехкратной экстраполяции, обусловлена только ошибками округления. Эти ошибки имеют большее значение, чем при применении метода Ромберга, так как для получения экстраполированных значений с помощью-алгоритма приходится использовать разности более высокого порядка.
4.3. -Алгоритм
-алгоритм [7,8] заключается в построении-таблицы по следующим правилам:
,
,
,
(3.7)
где
,
.
Экстраполированные значения находятся в четных столбцах матрицы. (Для того чтобы получить 1-е экстраполированное значение, необходимо использовать 4 рассчитанных, для получения дважды экстраполированного нужно 4 экстраполированных один раз и т.д).
-алгоритм применяется для данных, соответствующих последовательному увеличению nна единицу (для последовательностей, представимых в виде суммы степенных функций отn). На рис. 3.3а представлены результаты применения-алгоритма к последовательности (2.26). Видно, что в отличие от-алгоритма-алгоритм не решает точно задачу выделения степенных слагаемых последовательности. Применение-алгоритма к последовательности сумм (2.2) позволяет достичь точности порядка 10-5-10-6приn=10-20. Дальнейшее уточнение ограничивается погрешностью округления.
|
а) |
б) |
Рис. 3.3. Результаты экстраполяции с помощью -алгоритма:
а) – к последовательности (2.26); б) – к последовательности сумм (2.2).
4.4. U-алгоритм
u-алгоритмпредполагает для ускорения сходимости последовательностиzi, (i=1,…,n) использовать формулу
,
где
.
(3.8)
Здесь может kизменяется от 2 доn-1, номер экстраполяции равенk-1. Экстраполированные значения получаются путем применения формулы (3.8) к последовательностиziначиная с номера 1, 2,…
Как и -алгоритм u-алгоритм применяется для данных, соответствующих последовательному увеличениюnна единицу или на константу. На рис. 3.4 представлены результаты примененияu-алгоритма к последовательностям (2.26) и (2.2). Особенностью данного алгоритма является то, что если начинать экстраполяцию не с первого номера, а со второго или большего, то результаты экстраполяции могут ухудшаться.
При использовании подпоследовательности zkh, приh=10, 1000 результаты экстраполяции практически не меняются (рис. 3.5а,б). Таким же свойством обладает и-алгоритм.
|
а) |
б) |
Рис. 3.4. Результаты экстраполяции с помощью u-алгоритма:
а) – последовательности (2.26); б) – последовательности сумм (2.2).
|
а) |
б) |
Рис. 3.5. Результаты экстраполяции данных с помощью u-алгоритма при увеличении числа слагаемых на постоянную величину:
а) – на 10; б) – на 1000.
В результате анализа рассмотренных методов экстраполяции и примеров их применения можно сформулировать следующие выводы.
Рассмотренные методы повторной экстраполяции при неизвестных порядках аппроксимации kjмогут быть весьма эффективно использованы для уточнения результатов расчетов и оценки их погрешности.
В сравнении с методами, использующими известные значения kj, погрешности экстраполяции и округления рассмотренных в разделе 4 методов имеют существенно большие величины.
-алгоритм, единственный из рассмотренных, решает задачу распознавания степенных слагаемых последовательности, член которой представим в виде конечной или бесконечной суммы таких слагаемых. Ошибка экстраполяции имеет порядок следующего (неучтенного) слагаемого. При использовании остальных алгоритмов ошибка экстраполяции может содержать степенные слагаемые, отсутствующие в сумме. Поэтому с помощью -алгоритма при решении конкретных задач часто удается угадать закон изменения показателей степениki. Но тогда эту информацию можно использовать, и при проведении дальнейших параметрических исследований данной задачи применять метод Ромберга, требующий меньших затрат ресурсов.