Методика введения и изучения иррациональных чисел.
1. Введение начинается с целесообразно подобранной задачи. Например: извлечение квадратного корня из положительного числа, не являющегося полным квадратом; каким числом выражается длина диагонали квадрата со стороной 1; чему равна сторона квадрата, если известно, что его площадь равна 3.
Практические задачи: задачи измерения; каждой ли точке координатной прямой соответствует рац число?
Изображение чисел на координатной прямой
П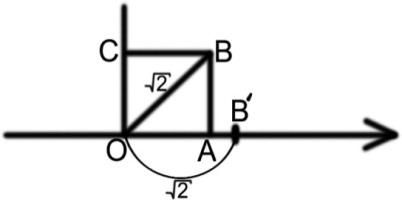
окажем,
что т. В’ соответствует числу, не явл
рацион, т. к. диагональ квадрата ОВ
несоизмерима с его стороной ОА
Д-во, что т. В не соотв. никакому рац числу
Т.
к. т. В’ находится на ОХ,
От
противного: пусть
– несократимая дробь. Обе части –
неотрицательны, возведем в квадрат,
получим:
,
,
=>
– четное, =>
– четное. Значит
можно представить в виде
.
Подставим в
:
=>
,
=>
– четное,
– четное. Тогда имеем
– четные. Это противоречит тому, что
– несократимая дробь. =>
=>
не
является рациональным числом.Таким
образом, число
можно изобразить на координатной прямой
некоторым числом, которое не является
рациональным. Такие числа называются
иррациональными.
2 подход
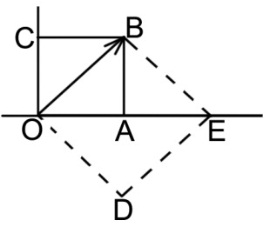
С
другой стороны
.
Если натуральное число не есть квадрат некоторого натурального числа, то оно есть квадрат иррационального числа. Таким образом, – иррациональное число.
3 подход
Иррациональные
числа – есть бесконечные десятичные
непериодические дроби. Так как
нельзя извлечь нацело
есть бесконечная десятичная непериодическая
дробь
есть число иррациональное.
4 подход
Рассмотрим приближенное значение с недостатком и с избытком:
С недостатком: 1,4; 1,41; 1,414; 1,4142
С избытком: 1,5; 1,42; 1,415; 1,4143
Объединим эти последовательности: 1,4< 1,41< 1,414 <1,4142 < < 1,4143 < 1,415 < 1,42 < 1,5
Докажем, что границей или пределом последовательностей является некоторое иррациональное число. Пусть границей явл , с другой стороны границей явл несократимая дробь .
Таким
образом, на границе последовательности,
представляющей квадраты членов,
последовательности приближений с
недостатком и с избытком находится с
одной стороны число 2, а с другой -
,
причем
=> данную последовательность определяют
два числа, не равные между собой, а это
невозможно => последовательности
определяют единственное число
.
Действия
над иррациональными числами:1)
сравнение (можно как десятичные дроби,
сравнивая кол-во единиц в соответствующих
разрядах, можно как квадраты корней);2)
сложение, вычитание, умножение, деление
(нельзя выполнять как с десятичными
дробями).
2.14Методика изучения процентов. Основные задачи на проценты в школьном курсе математики.
При изучение этого материала нужно сначала уч-мся объяснить, что такое сотая часть числа (напр, сотая часть метра – это см, сотая часть центнера – кг) надо отметить, что к этому времени уч-ся уже прошли деление и дроби, и у них не возникнет проблем. Люди давно заметили, что сотые доли величин удобны в практич д-ти (напр, при записи десятич дробей). Потому для них было придумано спец название – процент. Значит, а один см – один процент от 1м. Итак, 1 процент – это 1 сотая доля. Здесь важно обратить внимание на мат запись процентов " % ", и главное объяснить, что целая часть равна 100%. Также надо обратить внимание на свойства.
Свойства.
1)1% = А/100.
2)1%* 100 = А
Найти В процентов.
1% = А/100
В% = В*А/100
В*1% = В%
Пример найти 7% от числа 17.
7% от 17 будет 7*17/100 = 1.19 или одна целая девятнадцать сотых это семь процентов от семнадцати.
Также нужно отметить, что проценты это аналог обыкнов дробям ( 1/100 ) из этого следует, что процентами выполняются все 4 действия присущие обыкнов дробям. Так что при изучение темы проценты можно опираться на уже изученную тему по обыкновенным дробям.
Чтобы найти процентное отношение двух чисел А и В, надо отношение этих чисел умножить на 100%, то есть вычислить (а/в)*100%.