
- •Методика изучения начал систематического школьного курса планиметрии.
- •Методика изучения подобных треугольников.
- •Методика изучения основных соотношений между элементами треугольника.
- •Методика изучения понятия равенства фигур. Доказательство первых теорем планиметрии. Признаки равенства треугольников.
- •2.6 Методика изучения величин в школьном курсе планиметрии.
- •2.7Обобщение понятия степени в школьном курсе математики.
- •2.8 Исторические и логические последовательности изучения числовых множеств. Общий принцип расширения числовых множеств. Общая схема изучения новых чисел.
- •2.9Методика повторения и дальнейшего изучения натуральных чисел. Изучение обыкновенных и десятичных дробей.
- •2.10 Методика изучения тригонометрических функций в курсе планиметрии.
- •Методика изучения показательной и логарифмической функций в средней школе.
- •Методика введения и изучения рациональных чисел.
- •Методика введения и изучения иррациональных чисел.
- •2.14Методика изучения процентов. Основные задачи на проценты в школьном курсе математики.
- •2.15Методика изучения тождественных преобразований.
- •Методика изучения тригонометрических уравнений и неравенств в средней школе.
- •2.17Методика изучения показательных и логарифмических уравнений и неравенств в средней школе.
- •2.18Методика изучения уравнений и их систем в средней школе. Равносильность уравнений. Алгебраические уравнения и их системы.
- •Методика изучения неравенств и их систем в средней школе. Метод интервалов при решении неравенств.
- •Методика изучения функций. Понятие функций. Возможная методическая схема изучения функций в базовой школе. Методика изучения алгебраических функций.
- •Методика изучения числовых последовательностей и прогрессий.
- •Методика введения и изучения понятия производной в средней школе.
- •2.24Методика обучения школьников решению текстовых задач арифметическим методом и методом составления уравнений и неравенств.
- •2.25 Методические особенности изучения тригонометрических функций в средней школе. Построение графиков тригонометрических функций.
- •2.26 Использование понятия производной в курсе алгебры средней школы.
Методика изучения показательной и логарифмической функций в средней школе.
Ознакомление учащихся с показательной и логарифмической функциями начиная с изучения свойств степеней и логарифмов.
Курс
алгебры знакомит учащихся с понятием
степени с рациональным показателем.
Таким образом для любого основания
степени
 (где
(где
 ,
,
 )
можно построить функцию:
)
можно построить функцию:
 ,
,
 ,
область определения которой – множество
действительных чисел. Необходимо ввести
определение степени с иррациональным
показателем. Используемое свойство
степени с основным, например, большим
единицы (возрастании), рациональное
приближение иррационального числа α:
r1<
α< r2.
Исходя из графического изображения
зависимости показателя степени и
значения степени, показывается, что
найдется такое значение y,
которое будет наибольшим среди всех
ar1
и наименьшим среди всех ar2
, которое можно считать значением aα.
,
область определения которой – множество
действительных чисел. Необходимо ввести
определение степени с иррациональным
показателем. Используемое свойство
степени с основным, например, большим
единицы (возрастании), рациональное
приближение иррационального числа α:
r1<
α< r2.
Исходя из графического изображения
зависимости показателя степени и
значения степени, показывается, что
найдется такое значение y,
которое будет наибольшим среди всех
ar1
и наименьшим среди всех ar2
, которое можно считать значением aα.
Затем формируется определение показательной функции: функция, заданная формулой y=ax ( , ), называется показательной функцией с основанием a, и формулируемые основные свойства: D(ax)=R; E(ax)=RТ; ax возрастает при a>1 и ax убывает при 0<a<1; напоминаются основные свойства степеней. Т.о. показательная функция есть систематизация, обобщение и расширение знаний учащихся о свойствах степени.
Логарифмическая функция – новый математический объект для учащихся. К понятию логарифма учащихся подводят в процессе решения показательного уравнения ax=b в том случае, если b нельзя представить в виде степени с основанием a. Наше уравнение в случае b>0 имеет единственный корень, который называют логарифмом b по основанию a и обозначают logab, т.е. alogab=b. Одновременно с введением нового понятия учащиеся знакомятся с основным Логарифмическим тождеством. При работе с логарифмами применяются следующие их свойства, вытекающие из свойств показательной функции:
При любом ( ) и любых положительных x и y, выполнены равенства:
1. loga1=0
2. logaa=1
3. logaxy= logax+ logay
4. logax/y= logax- logay
5. logaxp= plogax
Изучение
логарифмической функции начинается с
выделения определения: функцию, заданную
формулой
 называют логарифмической функцией с
основанием
.
Основные свойства выводится из свойств
показательной функции:
называют логарифмической функцией с
основанием
.
Основные свойства выводится из свойств
показательной функции:
1.
 ,
,
2.
 ,
,
3. Логарифмическая функция на всей области определения возрастает (при a>1) или убывает (при 0<a<1).
Покажем,
что
при a>1
возрастает. Пусть
 и
и
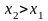 ,
надо доказать, что:
,
надо доказать, что:
 .
Допустим противное, т.е. что
.
Допустим противное, т.е. что
 .
Т.к. показательная функция
.
Т.к. показательная функция
 при a>1
возрастает, то из неравенства
следует:
при a>1
возрастает, то из неравенства
следует:


 ,
что противоречит выбору
,
что противоречит выбору
 .
Следовательно:
и функция
при a>1
– возрастает.
.
Следовательно:
и функция
при a>1
– возрастает.
Т.к. при a>1 функция возрастает, то логарифмическая функция положительна при x>1 и отрицательна для 0<x<1 (для основания 0<a<1 – наоборот). На основании рассмотренных свойств строится график этой функции.
Методика введения и изучения рациональных чисел.
Большинство применений в математике связано с измерением величин, но для этих целей не достаточно мн-ва натуральных чисел. т.к. не всегда единица величины (1м, см) укладывается в целое число раз в измеряемой величине. Поэтому для решения задач измерения величины необходимо рассмотреть мн-во N чисел. 1) первичным расширением этого мн-ва является мн-во положительных рациональных чисел. 2) зетем мн-во положительных действительных чисел и далее введем мн-во всех действительных чисел.
Пон-е
дроби. Пон-е положительного рационального
числа. Рассмотрим
задачу измерения длины отрезка. Пусть
дан отрезок
![]() предположим что при измерении оказалось,
что отрезок а
состоит из 2х отрезков е
в
этом случае длина отрезка а не может
быть выражена N
числом. Разобьем отрезок е на несколько
равных частей предположим на 3 и если
1/3 доля отрезка е укладывается в а
например 8 то в этом случае говорят, что
отрезок а соответствует пара чисел
(8,2) такая запись 8/3 называется дробной.
В общем случае отрезку а.
будет соотвествовать дробь m/n
т.е. отрезок а=m/n
отрезка е.
n
– знаменатель. он показывает на сколько
равных частей были разбит единичный
отрезок. m-
числитель. он показывает сколько частей
равных n
–ой части отрезка e
состоит отрезок а.
Дробь m/n
называется правильной если ее числитель
меньше знаменателя. и неправильной если
числитель больше знаменателя или равен
ему. 1/3 правильная. 3/3 неправильная.
предположим что при измерении оказалось,
что отрезок а
состоит из 2х отрезков е
в
этом случае длина отрезка а не может
быть выражена N
числом. Разобьем отрезок е на несколько
равных частей предположим на 3 и если
1/3 доля отрезка е укладывается в а
например 8 то в этом случае говорят, что
отрезок а соответствует пара чисел
(8,2) такая запись 8/3 называется дробной.
В общем случае отрезку а.
будет соотвествовать дробь m/n
т.е. отрезок а=m/n
отрезка е.
n
– знаменатель. он показывает на сколько
равных частей были разбит единичный
отрезок. m-
числитель. он показывает сколько частей
равных n
–ой части отрезка e
состоит отрезок а.
Дробь m/n
называется правильной если ее числитель
меньше знаменателя. и неправильной если
числитель больше знаменателя или равен
ему. 1/3 правильная. 3/3 неправильная.
Вернемся к задачи: Если 1/3 часть отрезка е уложилась в отрезке а восемь раз то очевидно что 1/6 часть отрезка е уложится в отрезке а 16 раз. 1/9 24 раза. Вообще говоря длина- одного и того же отрезка а при заданном единичном отрезке е может выражаться различными дробями при чем если длин выражена дробью m/n то она может быть выражена и дробью m*n/n*k, k€ (к пренадлежит мн-ву нат. чисел) N. Две дроби выражающие длину одного и того же отрезка называются равными.
Как сравнивать дроби. Две дроби m/n и p/q будут равны – тогда и только тогда когда выполняется сл. равенство m/q и p/n. Пусть во мн. всех дробей введено отн-е «равенство» выясняем какими св-вами обладает это отношения: 1)рефлексивности. каждая дробь равна себе. m/n= m/n => mn=nm
2) симметричности (если одна дробь равна второй то вторая равна первой m/n=p/q => p/q=m/n 3) транзитивности. m/n=p/q^ p/q=а/в =>m/n=а/в -
Мн-во равных между собой дробей называются положительным рациональным числом а каждая дробь принадлежащая этому классу есть запись (представление этого числа мн-во всех положительных рациональных чисел обозначается Q+.
Положительное рац. число можно записать любой дробью из данного класса чаще всего оно записывается несократимой дробью. В каждом классе эквивалентности существует единственная несократимая дробь.
Арифметические действия во множестве рациональных чисел, их св-ва.
1. Сложение. Пусть положительное рац. числов r1 представлено дробью m/n, а положительное рациональное число r2 – дробью p/n (r1= m/n r2 = p/n) то их суммой называется положительное рациональное число которое представляется дробью m+p/n
св-ва сложения: 1) коммуникативные r1+r2=r2+r1 2) ассоциативный (r1+r2)+r3=r1+(r2+r3)
Докажим 1е св-во. r1= m/n, r2=p/n, r1+r2 = m+p/n, т.к. m+p=p+m т.о. r1+r2=r2+r1. r2+r1=p+m/n. Мы воспользовались коммуникативным законом сложения N чисел. т.к. m и p натуральные числа. 2
2) Умножение. Если r1= m/n, а r2 = p/q то их произведениям называется положительное число которое представляет собою mp/nq
Св-ва мн-ва Q+.1.Во множестве Q+ нет наименьшего элемента. (у мн-ва N – это 1) Предположим что существует наименьший элемент во мн-ве Q+ пусть это r1 записан дробью m/n, r1=m/n. составим число r2> r2=m/2n покажем что r2<r1, то r1-r2=m/n-m/2n=2m-m/2n=m/2n>0=>r1>r2.
2. Во мн-ве Q+ нет наибольшего элемента. Предположим что такое число существует пусть это r1=m/n, r2=2m/n, r1-r2=m/n-2m/n=-m/n<0 =>r1<r2, т.е. r2>r1
3. Мн-во Q+ упорядочено отн-е быть больше или быть меньше, т.к. эти отношения заданные во мн-ве Q+ являя отношениями строгого порядка. 4. Мн-во Q+ плотно в себе. т.е. между 2мя Q+ можно найти др. Q+.
Доли и дроби. 1)конструируем доли. 2)ученик записывает долю при этом поясняет что под чертой записываем число равных частей на к-е делятся объект. Равные части а над чертой –сколько таких частей мы взяли в нашем случае Доля. 3)Сравнение долей в нач. курсе мат. начинается только с использованием граф. моделей. Использование таблицы полосок. 4)обуч-е решению задач с долями а)нахождение числа по его доли. Пр. в матке было 15м. проволки израсходовали 1/3 из этого мотка сколько из этой проволоки израсходовали. с пом. модели. б)нахождение доли по числу. Пр. 3метра приходятся на ¼ часть проволоки в матке. Сколько всего метров проволоки в мотке.
Дроби. Этапы изучения этой темы аналогичны тем что были в теме доли. Обычно в этой теме вводят термины «числитель» и «знаменатель».
