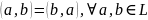20. Евклидовы пространства. Определение, примеры

ОПР: скалярное произведение двух векторов а и b в линейном пространстве L над полем Р - действительное число. Обозначается (а, b) и удовлетворяет следующим аксиомам:

1 (а, b) = (b, а) для любого а, b принадлежащего L

2 ((а + b), с) = (а, с) + (b, с) для любых а,b,c принадлежащих L

3 ((αa), b) = α (а, b) для любого а, b принадлежащего L, для любого α принадлежащего R

4 (а, а) ≥ 0, (а, а)= 0 в том и только том случае, если а = 0

Пример 1.

Пример 2 c[a;b] – пространство непрерывных функций на [a;b]

Пример3 В пространстве Rn x=(α1….αn) и y=(β1…βn)

Опред. Линейное пр-во L над полем R наз Евклидовым, если в нём определена операция скалярного произведения.

Замечание. В пр-ве L над полем С также может быть введено понятие скалярного произведения со свойствами:

1)x*y = ( )

2) (x1+x2)y = (x1,y) + (x2,y)

3) (λx1;y) = λ(x1;y)

4) (x;x)>=0, (x;x) = 0  x=

21. Свойства скалярного произведения, длина вектора, угол между векторами

Опред. Скалярным произведением 2-х векторов a, b в пр-ве над будем называть действительное число, кот. уд . следующим аксиомам:

1. 

2. 

3. 

4. 

Длиной вектора а в пр-ве над R наз. ; в : ; C : .

Теорема. В любом Евклидовом пр-ве справедливо нер-во Каши-Буняковского

Следствие.

Углом между векторами в произвольном Евклидовом пр-ве наз. угол , .

22. Ортонормированные системы векторов.

Опр. 1 вектора a,b в пр-ве наз ортогональными, если .

Лемма. Если некоторый вектор A ортогонален всем векторам пр-ва E, то это нулевой вектор.

, ,

1)Система векторов a1,a2, …,an(1) называется ортогональной, если (ai,…aj)=0(i=j); (ai,ai)>0, i=

2) система (1) называется ортонормированной, если она ортогональная и (ai,ai)=1, i=

Теорема. Ортогональные сис-мы ненулевых векторов линейно-независимы.

23.Метод ортогонализации Грамма – Шмидта.

Теорема: В n-мерном евклидовом пространстве существует ортонормированный базис.

Процесс построения ортогонального базиса к конечномерном Евклидовом пр-ве называется методом ортогонализации Грамма-Шмидта

В пр-ве многочленов не выше 2-й степени, требуется построить ортогональный базис a1= на .* *

,

Сис-ма: .

Эту систему можно нормировать

|b1| =

|b2|=

|b3|= =

Ортонормированная система e1= ; e2=t ; e3=

24, 25. Выражение скалярного произведения через координаты перемножаемых векторов. Матрица Грамма

Теорема. Если векторы a и b заданы своими координатами:a={X₁;Y₁;Z₁}, b={X₂;Y₂;Z₂}, то скалярное произведение опред. Формулой

ab=X₁X₂+Y₁Y₂+Z₁Z₂.

Скалярное произведение двух векторов равно сумме попарных произведений соответствующих координат этих векторов.

Следствие1. Необходимым и достаточным условием перпендикулярности векторов a и b является равенство: X₁X₂+Y₁Y₂+Z₁Z₂=0

Следствие2. Угол между векторами находится: cos f=

Слдствие3. Пр_us=XcosJ+YcosB+ZcosY

Определителем Грама системы векторов e₁, e₂, ..., e_n в евклидовом пространстве называется определитель матрицы Грама этой системы:

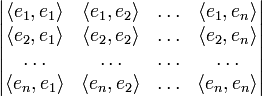
где   — скалярное произведение векторов e_i и e_j.

Матрица Грама возникает из следующей задачи линейной алгебры:

Пусть в евклидовом пространстве V система векторов e₁, e₂, ..., e_n порождает подпространство U. Зная, чему равны скалярные произведения вектора x из U с каждым из этих векторов, найти коэффициенты разложения вектора x по векторам e₁, e₂, ..., e_n. Исходя из разложения x = x₁e₁ + x₂e₂ + ... + x_ne_n получается линейная система уравнений с матрицей Грама:

Если базис ортонормированный, то матрица Грамма будет равна ед. матрице Е.

(x;y)=

При переходе к другому базису матрица Грамма является матрицей билинейной формы, меняется как матрица билинейной формы

Г’=T’ГT (T- матрица перехода от 1 базиса ко2)

Матрицу Грамма рассматривают не только для базисов, но и для произвольных наборов векторов.

Пусть матрица Грамма для a1….ak

1. Если векторы a1….ak – линейно независимы, то Г отлична от нуля.

2. Ранг Г равен количеству линейно-независимых векторов в системе a1….ak.

26. Нормированные векторные пространства Опр.: Говорят, что в линейном пр-ве L над полем R задана норма, которая каждому вектору х€L ставит в соответствие действительное число, которое обозначается так IIxII и удовлетворяет условиям: 1) IIλxII = λIIxII 2)IIxII ≥ 0, IIxII = 0 <=> x = 0 3)IIx+yII ≤ IIxII + IIyII – неравенство треугольника IIxII из пр-ва Rⁿ может быть определена такая: х = (α1…αn), IIxII = max I IαiI

Опр.: линейное пр-во, в котором введена норма называется нормированным. Теорема: евклидово пр-во является нормированным, если определить норму так IIxII = Док-во: первые 2 условия очевидны, докажем 3(н-во треугольника); рассмотрим норму: IIx + yII² = (x+y, x+y) = (x, x)+2(x,y)+(y,y) ≤ IIxII² + IIyII² = (IIxII + IIyII)² Следовательно, IIx + yII² ≤ (IIxII + IIyII)² , извлекая корни, получим неравенство треугольника.

27. Ортогональные матрицы и их свойства Матрица U называется ортогональной, если U^-1 = U^T Свойства: 1) det U = ±1 Док-во: det (U^-1U)= det E=1 det (U^-1U)=det(U^TU)=(det U)² =1 det U = ±1 2) если U1 и U2 ортогональны, то U1U2 = U также ортогональна Док-во: U1 -1 = U1T U2-1 = U2T UU^T = U1U2 = (U1U2)^T = U1U2U2^TU1^T = U1(U2U2^-1)U1^-1 =E 3) если столбцы матрицы U рассматривать как векторы из Rⁿ, то они образуют ортонормированный базис со скалярным произведением, равным сумме произведений соответствующих координат Док-во: U^TU=E ∑Uki Ukj = δij = Теорема: матрица перехода от одного ортонормированного базиса к другому ортогональна. Док-во: пусть Г, базис е1,е2…еn Г ’ , e1‘, e2’,…en’ тогда Г ‘ = Т^ТГ Т Г = Г ‘ = Е Т^Т Е Т = Е Т^ТТ = Е => Т^Т = Т^-1