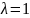- •2. Свойства линейных пространств
- •4Базис лин. Пр-ва, размерность. Коорд-ты.
- •5, 6 Матрич.Запись коо вект-в, изм. Коо при замене базиса
- •8. Изоморфизм векторных пространств, универсальный пример конечномерного векторного пространства.
- •9.Сумма и произведение линейных пространств
- •10. Линейный оператор, примеры, свойства.
- •11. Матрица лин. Оп-ра. Изменение матр. Оп-ра при замене базиса.
- •12. Действия над лин. Оп-ми. Матр. Суммы и произвед. Лин. Оп-ров.
- •13.Обратный лин. Оператор его матрица
- •14.Собственные векторы л.О., собств. Значения, характерист. Уравнение.
- •15.Правило нахождения собств. Векторов и собств. Значений
- •16 Модель бездефецитной торговли
- •17 Приведение матрицы линейного оператора к диагональному виду
- •18. Присоединенные векторы
- •19. Понятие о жордановой форме матрицы
- •20. Евклидовы пространства. Определение, примеры
- •21. Свойства скалярного произведения, длина вектора, угол между векторами
- •22. Ортонормированные системы векторов.
- •23.Метод ортогонализации Грамма – Шмидта.
- •28.Симметрические матицы и их свойства. Приведение симметрической матрицы к диагональному виду.
- •29.. Сопряж. Операторы и их св-ва.
- •33. Разложение произвольного линейного оператора в произведение самосопряженного оператора и изометрии.
- •34. Билинейная форма, ее матрица, изменение матрицы билинейной формы при изменении базиса.
- •35. Квадратичная форма и ее матричная запись.
- •36. Изменение матрицы квадратичной формы при линейной замене переменных, канонический вид квадратичной формы.
- •37. Приведение квадратичной формы к каноническому виду, закон инерции для квадратичных форм.
- •38 Положительно и отрицательно определенные квадратичные формы. Критерий Сильвестра.
13.Обратный лин. Оператор его матрица
Единичный (тождественный) оператор I действует по правилу I(x) = x ∀x ∈ V.
Л.О.(Лин.Оператор)
f−1
называется обратным по отношению к
Л.О. f,
если
 =f*
=I
(или можно
Е).
=f*
=I
(или можно
Е).
Теорема: для существования обратного оператора f необходимо и достаточно, чтобы f был взаимооднозначен.
Теорема: если А —
матрица линейного оператора в некотором
базисе, то
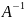 — матрица обратного оперетора в том же
базисе.
— матрица обратного оперетора в том же
базисе.
14.Собственные векторы л.О., собств. Значения, характерист. Уравнение.
Пусть f:Vn->Vn .
Опр.
Ненулевой вектор х Vn
наз-ся
собственным
вектором
оператора f,
если fx=λx(1),
где λ–некоторое
число (λ
P),
то λ
наз-ся собственным значением.
Vn
наз-ся
собственным
вектором
оператора f,
если fx=λx(1),
где λ–некоторое
число (λ
P),
то λ
наз-ся собственным значением.
Св-ва:1)Всякому собств. вектору отвечает одно собств. значение.
2)Собств. векторы, отвечающие собственным значениям — лин. независимы.
3)Мн-во всех собств. векторов, отвечающих одному собств. значению, дополненное нулевым вектором, образует лин-ые подпространства пространства Zn. Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор x имеет коорд. столбец X, то AX= λX или (A- λE)X=0. Можно записать в матричной форме: AX- λX, где X- матрица-столбец из коорд. вектора x.
Характ-им многочленом оператора f:Vn->Vn называется характеристический многочлен (xf (λ)=det(λE-Af)) его матрицы в некотором базисе. Характ-кий мн-н лин. оператора f не зависит от выбора базиса, в котором представлена его матрица. Уравнение Xf(λ)=0 называется характ-ким уравнением оператора f. Хар. ур-ние: (-1)nλn+an-1λn-1+…+a1λ+ a0=0 - Многочлен в левой части уравнения называется характ-ким мн-м. Характ. многочлен явл-ся многочленом n-ой степени. Теорема. Подобные матрицы имеют один и тот же характ. многочлен.
15.Правило нахождения собств. Векторов и собств. Значений
Выберем некоторый
базис e1,e2,e3,…,en
(1), тогда в этом базисе оператор f
будет иметь некоторую матрицу А,
и Х–координатный
столбец вектора. Тот факт, что х–собств.
значения, а
 –собств.
вектор оператора f,
то АХ= λХ;
(А– λE)X=0
(2). Система (2)–система линейных однородных
уравнений. Det(A–
λE)=0
(3). Решив ур-ние (3), получим характерист.
числа матрицы А.
Для нахождения собств. векторов, решим
систему: (A-
λE)X=0
.
–собств.
вектор оператора f,
то АХ= λХ;
(А– λE)X=0
(2). Система (2)–система линейных однородных
уравнений. Det(A–
λE)=0
(3). Решив ур-ние (3), получим характерист.
числа матрицы А.
Для нахождения собств. векторов, решим
систему: (A-
λE)X=0
.
16 Модель бездефецитной торговли
Пусть n
стран торгуют
между собой. Обозначим через
 нац-ный
доход i-той
страны;
нац-ный
доход i-той
страны;
 – это часть нац. дохода, которую j-тая
страна тратит на закупку товаров из
i-той
страны.
– это часть нац. дохода, которую j-тая
страна тратит на закупку товаров из
i-той
страны.
 +
+
 + … +
+ … +
 =
=

 =
=
 - это доля нац. дохода j-той
страны, кот-я тратится на закупку товаров
в i-той
стране.
- это доля нац. дохода j-той
страны, кот-я тратится на закупку товаров
в i-той
стране.
 = 1
= 1
C
элементами
составим матрицу:А =
 – структурная матрица международной
торговли
– структурная матрица международной
торговли
Сумма элементов по столбцам равна 1
Сумма элементов
по строкам:
 +
+
 + … +
+ … +
 =
=
 – все то, что покупают у i-той
страны => выручка i-той
страны в этой торговле.
– все то, что покупают у i-той
страны => выручка i-той
страны в этой торговле.

 .
не может
быть больше, чем
(доход)
.
не может
быть больше, чем
(доход)
 => АХ
= Х Х =
=> АХ
= Х Х =

Для бездефицитности
торговли нац. доходы стран должны быть
коорд-ми собственного вектора структурной
матрицы с собственным значением