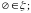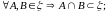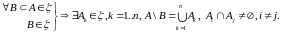- •1.Ортогональные и ортонормированные системы функций, ряды Фурье по ортого-
- •§1 Ортогональные системы функций. Ряды Фурье по ортогональным системам функций
- •Частичные суммы рядов Фурье: ядро Дирихле, формулы Дирихле.
- •3.Сходимость ряда Фурье в точке: Принцип локализации, условие Гёльдера, теорема
- •4.Равномерная сходимость ряда Фурье: Неравенство Бесселя, Теорема о равномерной
- •5.Сходимость семейства функций: определение равномерной сходимости семейства
- •6.Собственные интегралы с параметрами: свойства, теорема о дифференцировании
- •§1. Собственные интегралы с параметрами
- •7. Равномерная сходимость несобственного интеграла с параметрами: определение,
- •8. Свойства равномерно сходящихся несобственных интегралов: теоремы о предель-
- •9. Свойства равномерно сходящихся несобственных интегралов: теоремы о диффе-
- •10. Эйлеровы интегралы. Гамма-функция: определение, основное соотношение, про-
- •§3. Эйлеровы интегралы
- •11. Интеграл Фурье: определение, теорема (с леммами) о сходимости интеграла Фу-
- •§4 Интеграл Фурье
- •12. Преобразование Фурье: определение, свойства (ограниченность и непрерывность
- •§5. Преобразования Фурье
- •13. Теоремы о преобразовании Фурье и дифференцировании. Преобразование Фурье
- •14. Системы множеств: определения кольца, минимального кольца. Теорема о сущест-
- •§1 Системы множеств
- •15. Мера клеточных множеств. Теорема о полуаддитивности меры клеточных мно-
- •16. Внешняя мера, измеримые множества, мера Лебега. Свойства внешней меры.
- •17. Теорема о конечной аддитивности меры Лебега. Теорема о счетной аддитивности
- •18. Теорема о непрерывности меры Лебега. Какие множества измеримы по Лебегу?
- •19. Обобщение понятие меры Лебега на случай всей плоскости. Пример неизмеримого
- •20.Мера Лебега-Стилтьеса. Понятие абсолютно-непрерывной, дискретной и сингу-
- •21. Общее понятие меры. Продоление меры. Теорема о существовании и единственно-
- •§3 Общее понятие меры
- •22. Лебегово продолжение меры. Структура системы измеримых по Лебегу множеств.
- •§4. Лебегово продолжение меры
- •23. Измеримые функции: определения (X,y ) – измеримой, -измеримой, борелев-
- •24. Теорема об арифметических операциях с измеримыми функциями. Теорема об из-
- •25.Понятие сходимости почти всюду. Теорема Егорова.
- •26. Понятие сходимости по мере. Две теоремы о связи сходимости по мере и сходимо-
- •27. Простые функции: определение, теорема о простой функции. Необходимое и дос-
- •28. Интеграл Лебега для произвольных функций. Свойства интеграла Лебега. Теорема
- •29. Предельный переход в интеграле Лебега. Теорема Лебега (с док-вом). Теоремы
- •30. Понятие сигма-конечной меры. Интеграл Лебега по множеству бесконечной меры.
- •31. Сравнение интеграла Лебега с интегралом Римана.
- •32. Произведение мер. Формула для нахождения меры множества с помощью интегра-
- •§ 7 Произведение мер. Теорема Фубини.
- •33. Пространства суммируемых функций l1 и l2 . Теорема о полноте пространства l1.
- •§ 8 Пространства суммируемых функций.
§1 Системы множеств
Вспомним некоторые формулы, связанные с симметрической разностью множеств:
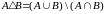
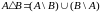
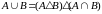
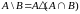
,
где
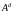 - дополнение.
- дополнение.
Определение
1. Непустая система множеств
 называется кольцом, если вместе
с любыми двумя множествами она содержит
их пересечение и симметрическую разность,
т.е.
называется кольцом, если вместе
с любыми двумя множествами она содержит
их пересечение и симметрическую разность,
т.е.
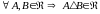 и
и
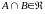 .
.
Условие
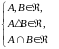 равносильно условию
равносильно условию
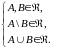 .
Это следует из формул, написанных выше
и
.
Это следует из формул, написанных выше
и
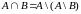 .
Таким образом, в определении кольца
вместо
.
Таким образом, в определении кольца
вместо
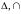 можно взять
можно взять
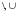 .
Т.е. кольцо - это система множеств,
замкнутая относительно операций
пересечения, объединения, разности и
симметрической разности двух (и любого
конечного числа) множеств.
.
Т.е. кольцо - это система множеств,
замкнутая относительно операций
пересечения, объединения, разности и
симметрической разности двух (и любого
конечного числа) множеств.
Если кольцо
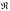 содержит хотя бы одно ненулевое
множество, то
содержит хотя бы одно ненулевое
множество, то
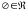 .
( Если
.
( Если
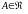
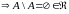 )
)
Пересечение любого числа колец является кольцом.
Примеры колец:
Множество ограниченных множеств из
 .
.
Множество измеримых по Жордану множеств.
Множество
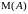 всех
подмножеств множества
всех
подмножеств множества
 .
Например, для
.
Например, для
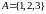 имеем
имеем
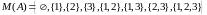 .
.
Любую систему множеств, не являющуюся кольцом, можно дополнить до кольца.
Определение
2. Пусть
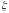 - система множеств,
- система множеств,
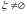 .
Кольцо
.
Кольцо
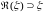 и такое, что
и такое, что
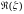 содержится
в любом кольце, содержащем
,
называется минимальным
кольцом над
или кольцом
порожденным
.
содержится
в любом кольце, содержащем
,
называется минимальным
кольцом над
или кольцом
порожденным
.
Примеры:
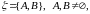
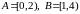 .
.
Тогда
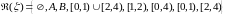
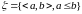 -
множество всех промежутков на прямой,
не является кольцом. Тогда
-
множество всех промежутков на прямой,
не является кольцом. Тогда
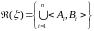 -
множество, состоящее из всевозможных
конечных объединений промежутков.
-
множество, состоящее из всевозможных
конечных объединений промежутков.
Теорема 1. Для любой непустой системы множеств существует и единственно минимальное кольцо .
Существование
докажем построением. Пусть
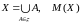 - система всех подмножеств множества
- система всех подмножеств множества
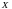 .
Пусть
.
Пусть
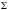 -
множество всех колец в
-
множество всех колец в
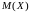 и содержащих
.
Тогда
и содержащих
.
Тогда
 - искомое минимальное кольцо над
.
- искомое минимальное кольцо над
.
Единственность очевидна, т.к. если бы минимальных кольца было два, то их объединение также было бы искомым кольцом. ■
Определение
3. Множество
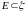 называется единицей
системы
,
если
называется единицей
системы
,
если
 .
.
Определение 4. Кольцо с единицей называется алгеброй множеств.
Если
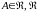 -
алгебра, то
-
алгебра, то
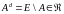 ,
т.е. алгебра множеств замкнута по
отношению с дополнению.
,
т.е. алгебра множеств замкнута по
отношению с дополнению.
Примеры:
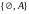 -
алгебра
с единицей А.
-
алгебра
с единицей А.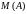 -
множество всех подмножеств А
– алгебра с единицей А.
-
множество всех подмножеств А
– алгебра с единицей А.Система всех конечных подмножеств множества А – кольцо, но алгебра только если А – конечно.
В
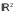 множество всех клеточных множеств
лежащих внутри
множество всех клеточных множеств
лежащих внутри
 -
алгебра с единицей
.
-
алгебра с единицей
.
Определение 5. Система множеств называется полукольцом если:
Примеры:
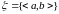 -
полукольцо.
-
полукольцо.В множество всех прямоугольников образуют полукольцо.
На
полукольце
минимальное
кольцо строится просто: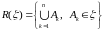 .
.
Определение
6. Кольцо
множеств называется
 -кольцом,
если:
-кольцом,
если:
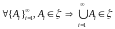 .
Кольцо множеств называется
.
Кольцо множеств называется
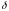 -кольцом,
если:
-кольцом,
если:
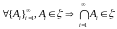 .
.
-алгеброй называется -кольцо с единицей.
-алгеброй называется -кольцо с единицей.
Замечание: понятия -алгебры и -алгебры равнозначны.
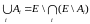 ,
,
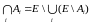 ■
■
Примеры:
- -алгебра.
Множество клеточных множеств внутри прямоугольника не является -алгеброй.
Определение.
Минимальной
алгеброй (
-алгеброй)
над
называется
алгебра (
-алгебра)
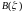
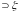 и содержащаяся в
и содержащаяся в
 алгебре
(
-алгебре),
содержащей
алгебре
(
-алгебре),
содержащей
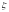 .
.
Определение.
Пусть
-множество
всех отрезков
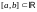 .
Борелевским
множеством
называется элемент борелевской
-
алгебры
.
Борелевским
множеством
называется элемент борелевской
-
алгебры
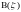 , т.е. минимальной
-алгебры
над
.
, т.е. минимальной
-алгебры
над
.