29. Предельный переход в интеграле Лебега. Теорема Лебега (с док-вом). Теоремы

Леви и Фату (без док-ва).

_{П.4. Предельный переход в интеграле Лебега}

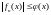_{Теорема 7 (Лебега). Пусть на , , интегрируема на . Тогда интегрируема на и} .

_{□ интегрируема на , интегрируема на}

_{Для =>}

_{По т. Егорова возьмем 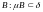и на :}

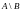_Т.е.

■

_{Теорема 8 (Леви). Пусть интегрируема на и} . _{Тогда, почти везде, на , интегрируема на и} .

_{Следствие}

_{Если и ряд сходится, то почти везде на}

_{сходится и}

_{Теорема 9 (Фату). Пусть измеримая функция, (почти везде) на и , то интегрируема на и} .

30. Понятие сигма-конечной меры. Интеграл Лебега по множеству бесконечной меры.

П. 5. Интеграл Лебега по множеству бесконечной меры

Мера , определённая на множестве называется - конечной, если , - конечна.

Последовательность множеств называется исчерпывающей на , если - конечно и .

Опр. Измеримая функция называется интегрируемой (суммируемой) на с - конечной мерой , если она интегрируема на множестве , - конечна и исчерпывающей последовательности

и он не зависит от выбора

Утверждения.

1. Для интегрирования простой функции необходимо и достаточно, чтобы каждое ненулевое значение она принимала на множестве конечной меры.

2. Из того, что сходится равномерно к , - интегрируема на

3. Из ограниченности функции не следует её интегрируемость.

31. Сравнение интеграла Лебега с интегралом Римана.

П. 6. Сравнение интеграла Лебега с интегралом Римана

Пусть - классическая мера Лебега.

Теорема 10. Если , то - интегрируема по Лебегу на и

Разбиение на частей точками

Суммы Римана-Дарбу:

Пусть:

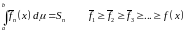
По Теореме Леви: и

почти всюду.

∎

Утверждения:

1. Если и несобственный интеграл , то

2. Если несобственный интеграл сходится абсолютно , то

3. Если несобственный интеграл сходится условно, то интеграл Лебега не существует.

Пример: - сходится условно, т.к. расходится

32. Произведение мер. Формула для нахождения меры множества с помощью интегра-

ла. Теорема Фубини (без док-ва).

§ 7 Произведение мер. Теорема Фубини.

Пусть - полукольца.

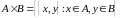- полукольцо.

- мера на , - аддитивная.

- мера на , - аддитивная.

Тогда - мера , - аддитивная.

- измеримо.

Теорема Фубини. Пусть , интегрируема по мере на , тогда

₍без доказательства).

33. Пространства суммируемых функций l1 и l2 . Теорема о полноте пространства l1.

§ 8 Пространства суммируемых функций.

Пусть на задана мера - полная.

Разобьем множество функций на на классы эквивалентности на _.

П. 1. Пространство .

пространство суммируемых на функций, то есть

- линейное пространство.

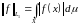
Теорема. Пространство - полное.

Пусть - фундаментальная последовательность

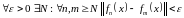
Выберем сходится. по следствию из теоремы Леви - сходится почти всюду. сходится почти всюду.

Докажем, что

- фундаментальна

по теореме Фату , то есть ∎

_Опр. Множество называется плотным в множестве , если любая окрестность любой точки из множества содержит точку из множества _.

_{Например,} плотно в _.

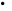в всюду плотно множество интегрируемых функций с конечным числом значений.

в всюду плотно множество интегрируемых непрерывных функций.

Опр. Мера называется мерой со счетным базисом, если счетная система измеримых множеств , такая что для измеримого

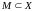
Пример: на отрезке счетным базис ­– множество промежутков с рациональным и концами (и их объединениями).

Опр. Пространство называется сепарабельным, если в нем существует счетное всюду плотное множество.

Если мера - мера со счетным базисом , то - сепарабельно.

Счетное всюду плотное множество:

- индикатор множества или характеристическая функция множества.

Счетное всюду плотное множество для

множество многочленов с рациональными коэффициентами

тригонометрическая система функций

П. 2. Пространство

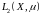- множество функций с интегрируемым квадратом, то есть

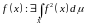
Свойства

∎

- интегрируема ∎

- линейное пространство.

Неравенство Коши — Буняковского.

Неравенство Минковского.

- полное без доказательства. ∎

- сепарабельно. (для со счетным базисом).

Для счетное всюду плотное множество – ортогональная тригонометрическая система.

Для многочлены Эрмита.

в интеграле