60.Что такое многокритериальная задача?

Задача с несколькими целевыми функциями. Она не имеет решения.

61.Что такое рекорд в методе ветвей и границ?

Рекорд - граничное значение целевой функции; наилучшее из найденных решений.

62.Приведите пример задачи целочисленного линейного программирования

Решить задачу ЦЛП:

f(x₁,x₂)= 2x₁+3x₂ → max,

5x₁+7x₂ ≤ 35,

4x₁+9x₂ ≤ 36,

x₁, x₂ ≥ 0,

x₁,x₂ - целые

Задачу решить можно методом прямого перебора. Организуем 2 цикла: 1-й по x1 от 0 до 9, 2-й, встроенный в первый, - по x2 от 0 до 5. Оператор тела цикла проверяет, удовлетворяет ли точка (x₁, x₂) обоим неравенствам, вычисляется значение функции f(x₁, x₂) и сравнивается с запомненным наилучшим решением

63. Приведите пример задачи параметрического линейного программирования.

Параметрическое программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров.

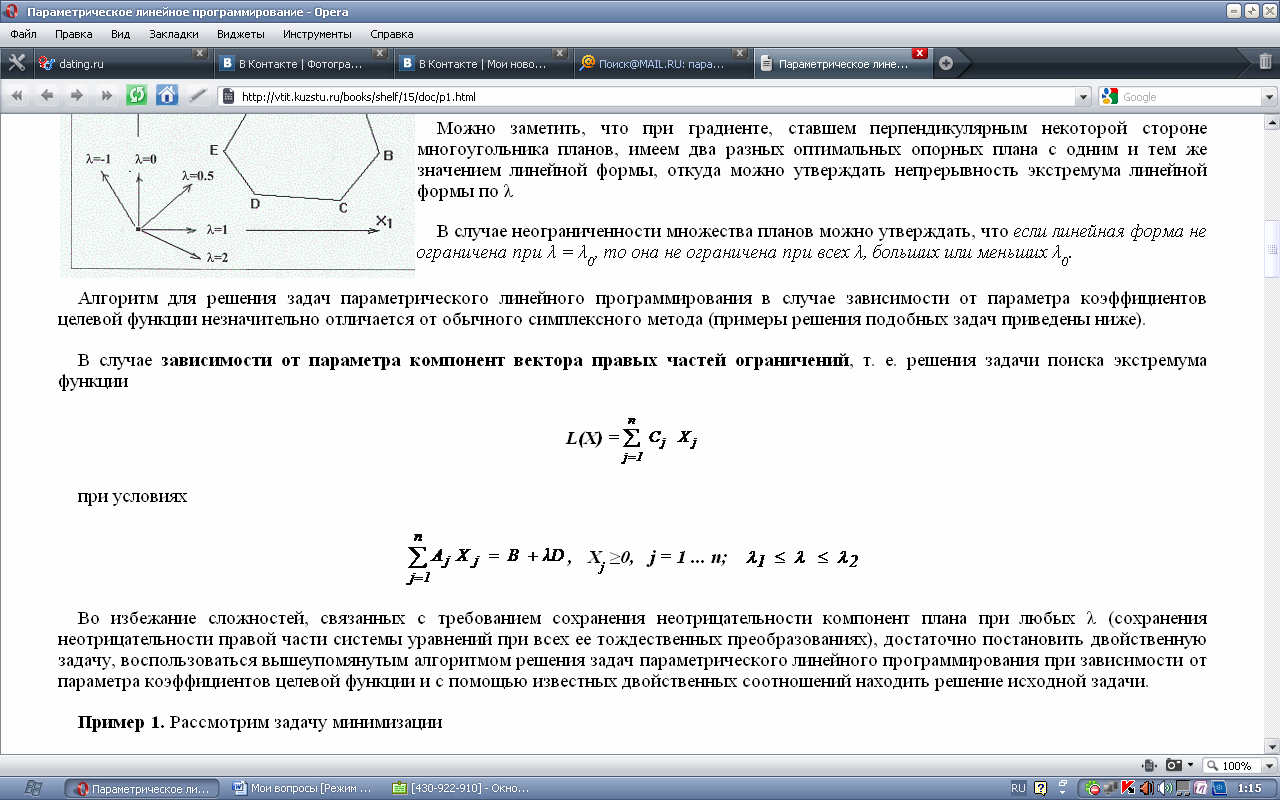
Рассмотрим задачу параметрического линейного программирования, в которой только коэффициенты целевой функции линейно зависят от некоторого единственного параметра λ (времени, температуры и т. п.):

О тыскать максимум (или минимум) функции:

при условиях:

64.Приведите пример многокритериальной задачи

М атематически такая задача содержит область допустим реш-ий, кот может иметь любую природу, и нес-ко целевых ф-ций, значение которых должно максимизироваться или минимизироваться в данной области. Максимизация или минимизация целевых ф-ций сводится друг к другу умножением на -1, поэтому, не нарушая общности, можно считать, что данная задача имеет вид: (x) max (i=1,2,…,n),

x D, (1)

x - ?,

где D – область допустим реш-ий. При этом в задаче x может быть векторным параметром. Если кол-во целевых функций (x) в задаче (1) больше одной, то данная задача явл зад-ей многокритериальной оптимизации. В экономических задачах допустим обл обычно задаётся системой ур-ний и неравенств, к которой могут быть добавлены некотор дополнит ограничения, например, ограничения на целочисленность переменных.

Пример. Парикмахерская может производит 2 вида продукции: муж и жен причёски, причём мастера, работающие в парик-ой явл-ся универсалами. Жен прич отнимает 2 ч работы мастера и приносит 10 у.е. прибыли. Муж прич отним 1 ч раб-ы и приносит 4 у.е. прибыли. Общий рес-с работы мастеров сост 40ч. Соц заказ, установленный для парик-ой при её открытии, состоит в максимальном кол-ве обслуженных клиентов. Если через x₁ и x₂ обознач кол-во муж и жен причёсок, сделанных в прарик-ой за рассматрив промежутов времени, то матем модель задачи имеет след вид: z₁= 4x₁+10x₂ → max

z₂= x₁ + x₂ →max

x₁+2x₂ ≤ 40

x₁, x₂ Z

x₁, x₂ ≥0

x₁, x₂ - ?

В дан задаче оптимальность производстен плана парик-ой опред-ся по 2 критериям: критерию максим прибыли и критерию максим кол-ва обслуженных клиентов. Этим критериям соответствуют целевые ф-ции z₁ и z_{2 .}

В задаче многокритериальной оптимизации (1), как правило, нет решений, поскольку цели, выражен различн критериями, часто явл-ся противоположными. Поэтому оптимальные значения целевых ф-ций достигаются при разных допустим реш-ях, кот нужно сравнивать, чтобы выбрать 1 допустимый вариант.