
- •Системы линейных уравнений. Разрешимость систем линейных уравнений (теорема Кронекера-Капелли).Методы решения.
- •Основные алгебраические структуры: группы, кольца , поля. Основные свойства. Примеры.
- •1. Гомоморфный образ группы также является группой относительно своей операции.
- •2. Пусть f: g1®g2 – гомоморфизм групп. Тогда
- •Композиция любых двух (или нескольких) гомоморфизмов (моно, эпи) является гомоморфизмом (моно, эпи).
- •Определители и их свойства. Основные методы вычисления определителей.
- •Линейные пространства, подпространства. Примеры. Свойства пространств. Линейная зависимость и независимость системы векторов. Базис пространства.
- •5. Линейные операторы. Собственные векторы и собственные значения линейного оператора, их свойства и отыскание.
- •6. Корни многочлена. Методы нахождения корней. Результант многочленов, его связь с корнями.
- •7. Поле комплексных чисел. Формула Муавра. Извлечение корня из комплексных чисел.
- •8. Линии второго порядка, их канонические уравнения, фокусы, директрисы, асимптоты.
- •9. Прямая и плоскость в пространстве, их уравнения. Взаимное расположение прямых и плоскостей.
- •10. Проективная плоскость. Координаты точки и прямой. Особенности линий второго порядка.
- •11. Операции над векторами векторного пространства v3. Векторный метод в решении геометрических задач.
- •12. Предел непрерывность функций одной и нескольких переменных. Свойства функций, непрерывных на отрезке.
- •13. Производная и дифференциал функции одной и нескольких переменных. Достаточные условия дифференцируемости.
- •14. Определенный интеграл, его свойства. Основная формула интегрального исчисления.
- •15. Числовые ряды. Абсолютная и условная сходимость. Признаки сходимости: Даламбера, интегральный, Лейбница.
- •18. Производная функция комплексного переменного. Условия Коши-Римана. Аналитическая функция.
- •19. Степенные ряды в действительной и комплексной области. Радиус сходимости.
- •20. Ряд Фурье по ортогональной системе функций. Неравенство Бесселя, равенство Парсеваля, сходимость ряда Фурье.
- •21. Уравнения в частных производных. Основные задачи математической физики. Метод Фурье.
- •23. Множества и способы их задания. Отношения и отображения. Понятие о мощности. Счетные и континуальные множества.
- •Свойства счетных множеств
- •Графическое представление
- •5. Основные тождества алгебры множеств
- •Принципы математической индукции
- •Отображение отношения функции
- •24. Коды постоянной и переменной длины, примеры их использования. Принцип работы архиватора.
- •25. Задача потребительского выбора и ее решение.
- •26. Понятие эластичности, геометрический смысл. Свойства эластичности, эластичность элементарных функций.
- •27. Производственная функция. Закон убывающей эффективности.
- •28. Транспортная логистика. Транспортная система России, ее особенности и характеристики. Маршруты движения автотранспорта. Математические методы для организации материала потока.
- •29. Задачи линейного программирования. Экономический анализ задач с использованием теории двойственности.
- •3) Двойственная задача.
- •30. Нелинейное программирование. Методы решения задач.
6. Корни многочлена. Методы нахождения корней. Результант многочленов, его связь с корнями.
Пусть
-
произвольный многочлен из кольца
![]() .
Пусть
.
Пусть
![]() - элемент из области целостности (область
без делителей нуля).
- элемент из области целостности (область
без делителей нуля).
![]() ,
,
![]() .
Сумму
.
Сумму
![]() называют значением многочлена
называют значением многочлена
![]() .
-
корень многочлена
,
если
.
-
корень многочлена
,
если
![]() .
.
Теорема Безу:
Пусть
![]() ,
,
тогда в кольце
существует многочлен
,
,
тогда в кольце
существует многочлен
![]() ,
что
,
что
![]() .
Другая формулировка теоремы Безу:
Остаток от делителя многочлена
на двучлен
.
Другая формулировка теоремы Безу:
Остаток от делителя многочлена
на двучлен
![]() равен значению многочлена
.
равен значению многочлена
.
Теорема: (Критерий
корня): Пусть
,
-
является корнем
тогда и только тогда, когда
![]() .
Доказательство. Необходимость: пусть
– многочлен, для которого
– корень. Докажем, что
.
Доказательство. Необходимость: пусть
– многочлен, для которого
– корень. Докажем, что
![]() .
По теореме Безу
.
По теореме Безу
![]() .
Достаточность:
.
Д-ть:
– корень.
.
Достаточность:
.
Д-ть:
– корень.
![]() ,
,
![]() .
Чтд.
.
Чтд.
Схема Горнера – это аппарат, который позволяет найти результат от деления многочлена на двучлен .
Пример. Выполнить деление по схеме Горнера.
Если – корень многочлена , то по критерию корня это означает, что .
Если
– корень многочлена
,
то
![]() ,
,
![]() ,
….
,
….
Может оказаться,
что
– корень многочлена
![]() и
т.д.
и
т.д.
Наибольшая натуральная степень двучлена , на которую делится многочлен , называется порядком кратности корня для многочлена .
Т.о.
является k-кратным
корнем ненулевого многочлена
в том и только том случае, если
![]() не
делится на
не
делится на
![]() .
Константа
есть k-кратный
корень многочлена
,
если
.
Константа
есть k-кратный
корень многочлена
,
если
![]() ,
не делится на
.
,
не делится на
.
Теорема: если многочлен f = anxn + an-1xn-1 + … + a1x + a0Z[x] имеет несократимую дробь p/q корнем, то: 1) р – делитель а0, а q – делитель аn. 2) p – mq – делитель f(m) для mZ.
Следствие: Если p/q – корень, то f(1)(p - q), a f(-1)(p + q). Замечание: данная теорема является лишь необходимым условием существования корня, а поэтому с помощью 1 условия можно найти все возможные корни, с помощью 2 условия можно отбросить некоторые, но в конечном итоге все они должны быть проведены по схеме Горнера.
Пример: Найти рац. корни многочлена 4х3 – 3х -1. р = {1}, q = {1, 2, 4}. p/q = {1, ½, ¼}. f(1) = 0. f(-1) = -2.
корни |
½ |
-½ |
¼ |
-¼ |
(-2/(p + q))Z |
- |
+ |
- |
- |
4 0 -3 -1
-½ 4 -2 -2 0
-½ 4 -4 0
-½ 4 -6
Ответ: данный многочлен имеет 2 рац. корня: простой корень -1 и двукратный корень -½.
Нахождение корней многочлена над полем действительных чисел.
Нахождение корней многочлена над полем рациональных чисел.
Решение уравнений.
Уравнением 3-й
степени называется уравнение вида
![]() (1), где
(1), где
![]() ,
,
![]() .
Комплексное число
- называется корнем этого уравнения,
если:
.
Комплексное число
- называется корнем этого уравнения,
если:
![]() .
.
Преобразуем
уравнение (1) в уравнение (2):
![]() (2).
(2).
![]() ,
,
![]() .
.
![]()
![]() .
.
Обозначим:![]() ,
,
![]() ,
,
![]() (3). Такое уравнение называют приведенным
кубическим уравнением.
(3). Такое уравнение называют приведенным
кубическим уравнением.
Пусть имеется
приведенное кубическое уравнение
![]() (*). Введем обозначения
(*). Введем обозначения
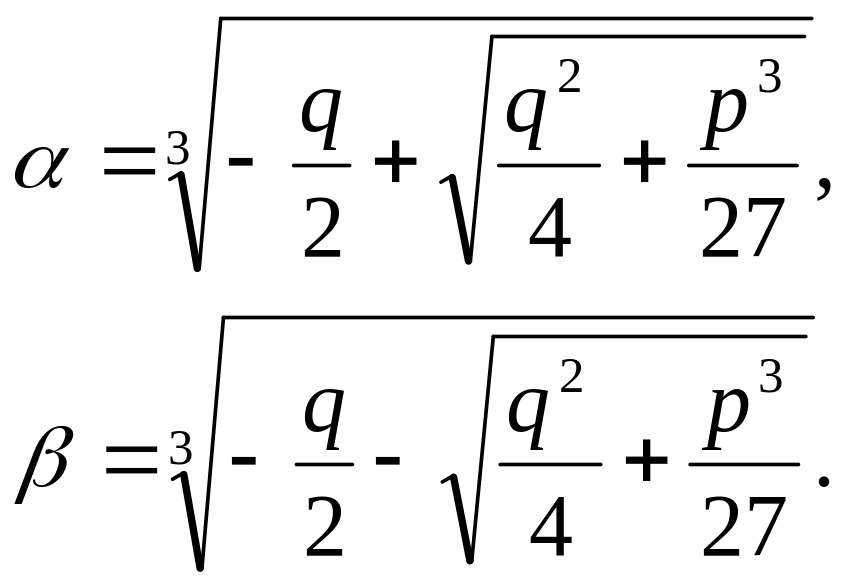 .
Это формулы Кардано.
.
Это формулы Кардано.
Теорема. Корни
уравнения (*) выражаются формулами:
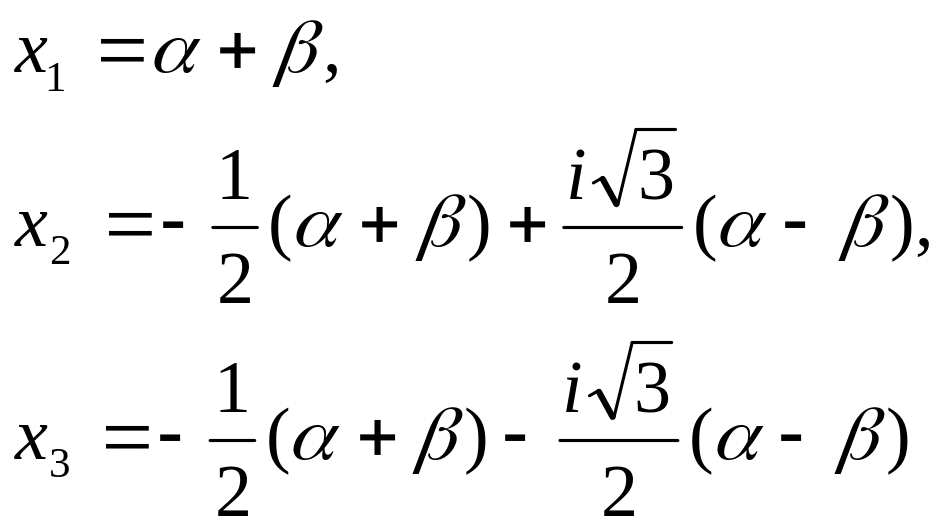
Пример. Решить уравнение 3 степени.
Уравнение 4-й степени. Метод Феррари.
![]() - уравнение 4-й
степени,
- уравнение 4-й
степени,
![]() .
Поделим на
.
Поделим на
![]() :
:
![]() .
.
Рассмотрим метод Феррари решения уравнения такого вида:
1.
![]() .
.
2. Дополним левую часть до полного квадрата.
![]()
![]() .
.
3. Дополним левую
часть до полного квадрата, дополняя
слагаемые с новой переменной
![]() .
.
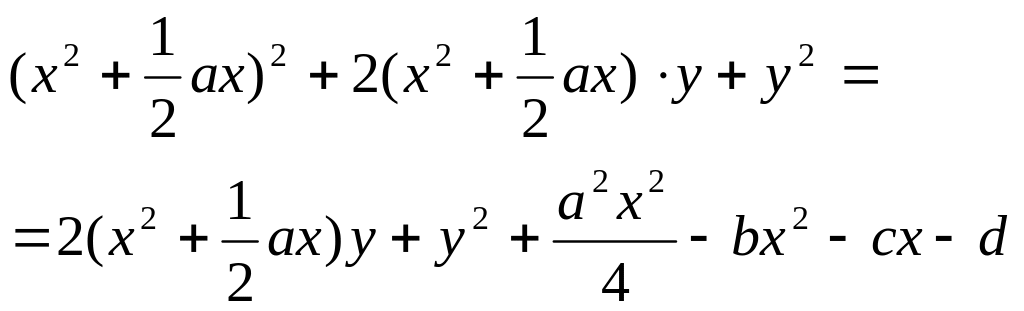
![]() .
.
4. Поскольку в левой части полный квадрат, следовательно, это уравнение имеет 2-х кратный корень, а это возможно, когда у уравнения в правой части Д=0.
![]() .
.
5. Найдем некоторый
корень кубического уравнения, относительно
.
Пусть это число
![]() .
Подставим его в уравнение пункта 3. В
правой части появится полный квадрат,
т.е. правая часть примет вид:
.
Подставим его в уравнение пункта 3. В
правой части появится полный квадрат,
т.е. правая часть примет вид:
![]() ,
,
![]() .
.
6. Последнее уравнение
преобразуется в дезъюнкцию:
![]()
![]() .
.
7. Решить полученные квадратные уравнения.
Пример. Решить уравнение методом Феррари.
Результантом
многочленов
![]() называется определитель, составленный
следующим образом.
называется определитель, составленный
следующим образом.
Пример:
Результант многочленов используется при решении систем уравнений.
