
- •Системы линейных уравнений. Разрешимость систем линейных уравнений (теорема Кронекера-Капелли).Методы решения.
- •Основные алгебраические структуры: группы, кольца , поля. Основные свойства. Примеры.
- •1. Гомоморфный образ группы также является группой относительно своей операции.
- •2. Пусть f: g1®g2 – гомоморфизм групп. Тогда
- •Композиция любых двух (или нескольких) гомоморфизмов (моно, эпи) является гомоморфизмом (моно, эпи).
- •Определители и их свойства. Основные методы вычисления определителей.
- •Линейные пространства, подпространства. Примеры. Свойства пространств. Линейная зависимость и независимость системы векторов. Базис пространства.
- •5. Линейные операторы. Собственные векторы и собственные значения линейного оператора, их свойства и отыскание.
- •6. Корни многочлена. Методы нахождения корней. Результант многочленов, его связь с корнями.
- •7. Поле комплексных чисел. Формула Муавра. Извлечение корня из комплексных чисел.
- •8. Линии второго порядка, их канонические уравнения, фокусы, директрисы, асимптоты.
- •9. Прямая и плоскость в пространстве, их уравнения. Взаимное расположение прямых и плоскостей.
- •10. Проективная плоскость. Координаты точки и прямой. Особенности линий второго порядка.
- •11. Операции над векторами векторного пространства v3. Векторный метод в решении геометрических задач.
- •12. Предел непрерывность функций одной и нескольких переменных. Свойства функций, непрерывных на отрезке.
- •13. Производная и дифференциал функции одной и нескольких переменных. Достаточные условия дифференцируемости.
- •14. Определенный интеграл, его свойства. Основная формула интегрального исчисления.
- •15. Числовые ряды. Абсолютная и условная сходимость. Признаки сходимости: Даламбера, интегральный, Лейбница.
- •18. Производная функция комплексного переменного. Условия Коши-Римана. Аналитическая функция.
- •19. Степенные ряды в действительной и комплексной области. Радиус сходимости.
- •20. Ряд Фурье по ортогональной системе функций. Неравенство Бесселя, равенство Парсеваля, сходимость ряда Фурье.
- •21. Уравнения в частных производных. Основные задачи математической физики. Метод Фурье.
- •23. Множества и способы их задания. Отношения и отображения. Понятие о мощности. Счетные и континуальные множества.
- •Свойства счетных множеств
- •Графическое представление
- •5. Основные тождества алгебры множеств
- •Принципы математической индукции
- •Отображение отношения функции
- •24. Коды постоянной и переменной длины, примеры их использования. Принцип работы архиватора.
- •25. Задача потребительского выбора и ее решение.
- •26. Понятие эластичности, геометрический смысл. Свойства эластичности, эластичность элементарных функций.
- •27. Производственная функция. Закон убывающей эффективности.
- •28. Транспортная логистика. Транспортная система России, ее особенности и характеристики. Маршруты движения автотранспорта. Математические методы для организации материала потока.
- •29. Задачи линейного программирования. Экономический анализ задач с использованием теории двойственности.
- •3) Двойственная задача.
- •30. Нелинейное программирование. Методы решения задач.
12. Предел непрерывность функций одной и нескольких переменных. Свойства функций, непрерывных на отрезке.
Определение. Пусть даны две переменные х и у. Переменная у называется функцией от переменной х, если каждому значению х из области его изменения ставится в соответствие по некоторому закону определенное значение у. Переменная х называется в этом случае аргументом функции у.
Пусть каждому натуральному числу n сопоставлено вещественное число, обозначенное xn. Тем самым нам заданы некоторые вещественные числа, определенным образом перенумерованные: х1 имеет номер 1, х2— номер 2, и т. д. Тогда говорят, что задана последовательность чисел, или числовая последовательность x1, x2, x3,…, xn.
Числа, составляющие последовательность, называются ее членами, а хn — общим или n-м членом последовательности.
Определение. Число
а называется пределом числовой
последовательности x1,
x2,
x3,…,
xn,
если для любого сколь угодно малого
положительного числа ε можно указать
такое натуральное число N,
что для всех членов последовательности
с номерами n > N выполняется неравенство
![]() .
.
Арифметические свойства пределов:
Если переменная хn имеет пределом число а, и а больше некоторого числа b, то значения переменной, начиная с некоторого n, будут также больше этого числа b.
Если переменная хn имеет пределом а, и а меньше некоторого числа с, то значения этой переменной, начиная с некоторого n, будут также меньше этого числа с.
Если переменная имеет предел, то он единственный. Иначе говоря, переменная не может иметь двух различных пределов.
Если имеем две переменные величины хn и уn, имеющие пределами соответственно числа а и b, причем хn = уn для всех n, то а = b.
Если переменные хn и уn имеют своими пределами соответственно числа а и b, причем хn ≤ уn для всех n, то a ≤ b.
Пусть имеем три переменные хn, уn и zn, связанные неравенствами хn ≤ уn ≤ zn для всех n. Тогда если переменные хn и zn имеют один и тот же предел а, то переменная уn также имеет предел и этот предел равен а.
Если множество значений переменной хn, начиная с некоторого значения n, ограничено, то хn является ограниченной величиной.
Если переменная хn имеет конечный предел, то она ограничена.

![]()
![]()
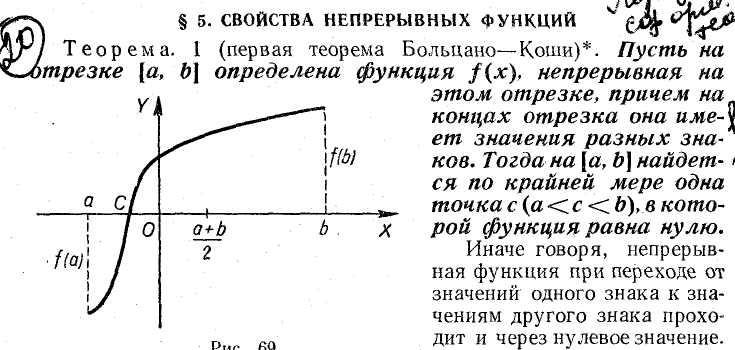


![]()

Определение Даны три переменные величины х, у и z. Если каждой паре значений независимых переменных х и у из области их изменения соответствует по некоторому закону определенное значение переменной z, то переменная z называется функцией двух независимых переменных х и у. Обозначение функции двух переменных следующее: z = f(х, у)
![]()

![]()

Теорема 3 (теорема Вейерштрасса об ограниченности функции). Если функция f(x, у) непрерывна в ограниченной замкнутой области (D), то f(x, у) ограничена в области (D).

![]()
![]()
13. Производная и дифференциал функции одной и нескольких переменных. Достаточные условия дифференцируемости.

![]()
![]()
![]()
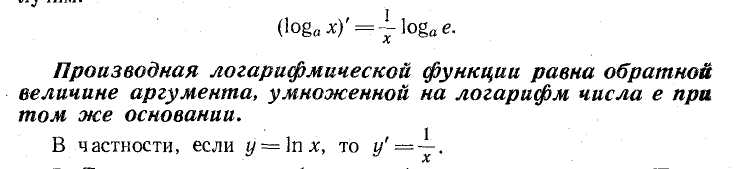
![]()
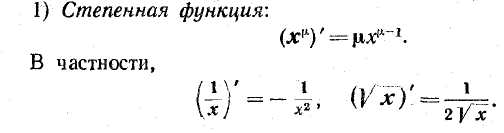



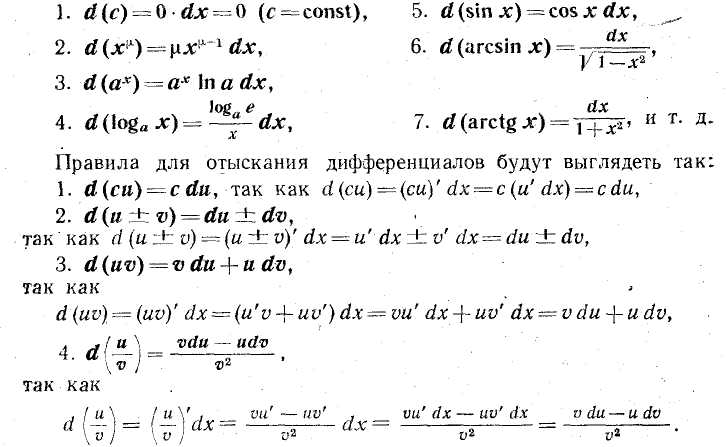
14. Определенный интеграл, его свойства. Основная формула интегрального исчисления.


![]()
![]()
![]()
![]()
![]()
![]()
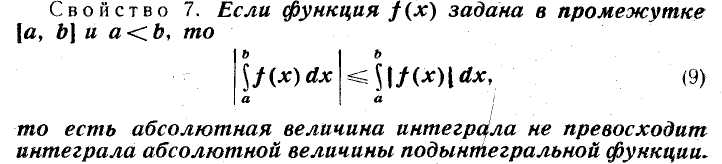
![]()
![]()

Функция
![]() называется первообразной функции
называется первообразной функции
![]() на интервале
,
если для любого
на интервале
,
если для любого
![]() выполняется равенство
выполняется равенство
![]() .
.
Теорема:
Если функция
является первообразной функции
на
,
то множество всех первообразных для
задается формулой
![]() ,
где
,
где
![]() - постоянное число.
- постоянное число.
Множество всех
первообразных функций
для
называется неопределенным интегралом
от функции
и обозначается символом
![]() .
.
Пусть функция
![]() определена на отрезке
определена на отрезке
![]() ,
.
Выполним следующие действия.
,
.
Выполним следующие действия.
1. С помощью точек
![]()
![]() разобьем отрезок
на
частичных отрезков
разобьем отрезок
на
частичных отрезков
![]() .
.
![]()
2. В каждом частичном
отрезке
![]() ,
,
![]() выберем произвольную точка
выберем произвольную точка
![]() и вычислим значение функции в ней, то
есть величину
и вычислим значение функции в ней, то
есть величину
![]() .
.
3. Умножим найденное
значение функции
на длину
![]() соответствующего частичного отрезка:
соответствующего частичного отрезка:
![]() .
.
4. Составим сумму всех таких произведений:
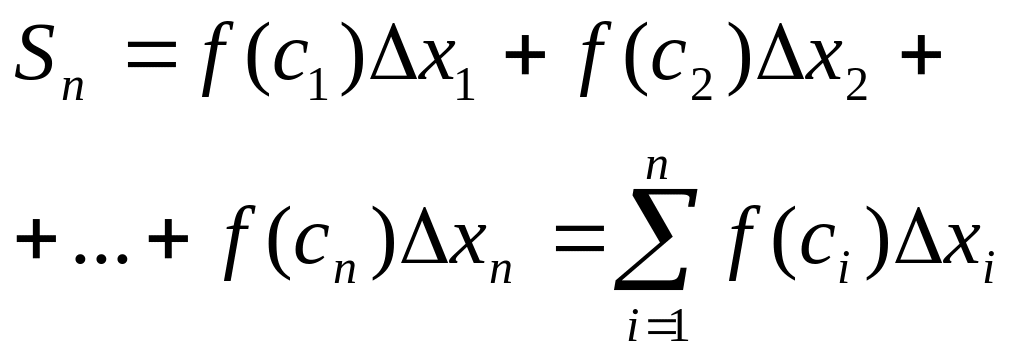 (1)
(1)
Сумма вида (1)
называется интегральной суммой функции
на отрезке
.
Обозначим через
длину наибольшего частичного отрезка:
![]() (
).
(
).
5. Найдем предел
интегральной суммы (1), когда
![]() так, что
так, что
![]() .
.
Если при этом
интегральная сумма
имеет предел
![]() ,
который не зависит ни от способа разбиения
отрезка
на частичные отрезки, ни от выбора точек
в них, то число
называется определенным
интегралом
от функции
на отрезке
и обозначается
,
который не зависит ни от способа разбиения
отрезка
на частичные отрезки, ни от выбора точек
в них, то число
называется определенным
интегралом
от функции
на отрезке
и обозначается
![]() .
Таким образом,
.
Таким образом,
![]() . (2)
. (2)
Числа a
и b
называются соответственно нижним и
верхним пределами интегрирования,
- подынтегральной функцией,
![]() - подынтегральным выражением,
- переменной интегрирования, отрезок
- областью (отрезком) интегрирования.
- подынтегральным выражением,
- переменной интегрирования, отрезок
- областью (отрезком) интегрирования.
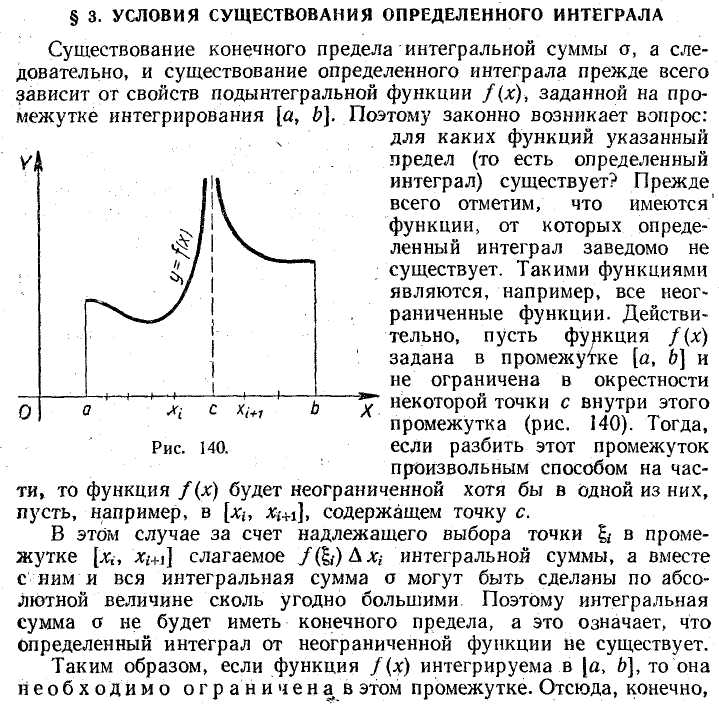
Функция , для которой на отрезке существует определенный интеграл , называется интегрируемой на этом отрезке.
Теорема (Коши): Если функция непрерывна на отрезке , то определенный интеграл существует.
Непрерывность функции является достаточным условием интегрируемости.
Свойства, вытекающие из определения определенного интеграла:
1. Определенный
интеграл не зависит от обозначения
переменной интегрирования:
![]() .
Интегральная сумма и ее предел не зависят
от того, какой буквой обозначается
аргумент данной функции.
.
Интегральная сумма и ее предел не зависят
от того, какой буквой обозначается
аргумент данной функции.
2. Определенный
интеграл с одинаковыми пределами
интегрирования равен нулю:
![]() .
.
3. Для любого
действительного числа
:
![]() .
.
Формула Ньютона-Лейбница.
Пусть функция интегрируема на отрезке .
Теорема.
Если функция
непрерывна на отрезке
и
- какая-либо ее первообразная на
(
),
то имеет место формула
![]() (3).
(3).
Доказательство:
Разобьем отрезок
точками
![]() на
частичных отрезков
на
частичных отрезков
![]() как показано на рисунке.
как показано на рисунке.
Рассмотрим тождество
![]()
Преобразуем каждую
разность в скобках по формуле Лагранжа
![]() .
Получим
.
Получим
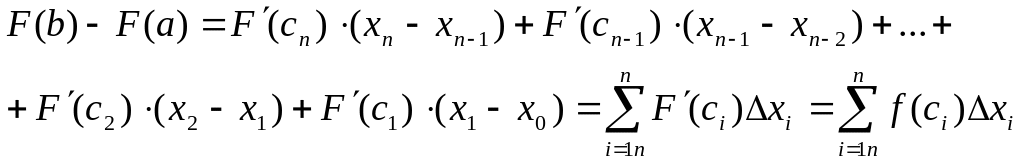 ,
т.е.
,
т.е.
![]() , (2)
, (2)
где
![]() некоторая точка интервала
некоторая точка интервала
![]() .
Так как функция
непрерывна на
,
то она интегрируема на
.
Поэтому существует предел интегральной
суммы, равный определенному интегралу
от
на
.
.
Так как функция
непрерывна на
,
то она интегрируема на
.
Поэтому существует предел интегральной
суммы, равный определенному интегралу
от
на
.
Переходя в равенстве
(2) к пределу при
![]() ,
получаем
,
получаем
![]() ,
т.е.
,
т.е.
![]() .
Доказано.
.
Доказано.
Основные свойства определенного интеграла.
Пусть функция интегрируема на отрезке .
1. Если
- постоянное число и функция
интегрируема на отрезке
,
то
![]() .
.
2. Если функции
![]() и
и
![]() интегрируемы на
,
тогда интегрируема на
их сумма и
интегрируемы на
,
тогда интегрируема на
их сумма и
![]() ,
т.е интеграл от суммы равен сумме
интегралов.
,
т.е интеграл от суммы равен сумме
интегралов.
3.
![]() .
.
![]() .
.
4. Если функция
интегрируема на отрезке
и
![]() ,
то
,
то
![]() ,
то есть интеграл по всему отрезку равен
сумме интегралов по частям этого отрезка.
,
то есть интеграл по всему отрезку равен
сумме интегралов по частям этого отрезка.
5. «Теорема о
среднем». Если функция
непрерывна на отрезке
,
то существует точка
![]() такая, что
такая, что
![]() .
.
![]() - называется средним значением функции
на отрезке
.
- называется средним значением функции
на отрезке
.
6. Если функция
сохраняет знак на отрезке
,
где
,
то интеграл
![]() имеет тот же знак, что и функция. Так,
если
имеет тот же знак, что и функция. Так,
если
![]() на отрезке
,
то
на отрезке
,
то
![]() .
.
7. Неравенство между
непрерывными функциями на отрезке
,
можно интегрировать. Так, если
![]() при
при
![]() ,
то
,
то
![]() .
.
8. Оценка интеграла. Если m и M – соответственно наименьшее и наибольшее значения функции на отрезке , то
![]() .
.
9. Модуль определенного
интеграла не превосходит интеграла от
модуля подынтегральной функции:
![]() ;
.
;
.
10. Производная
определенного интеграла по переменному
верхнему пределу равна подынтегральной
функции, в которой переменная интегрирования
заменена этим пределом, то есть
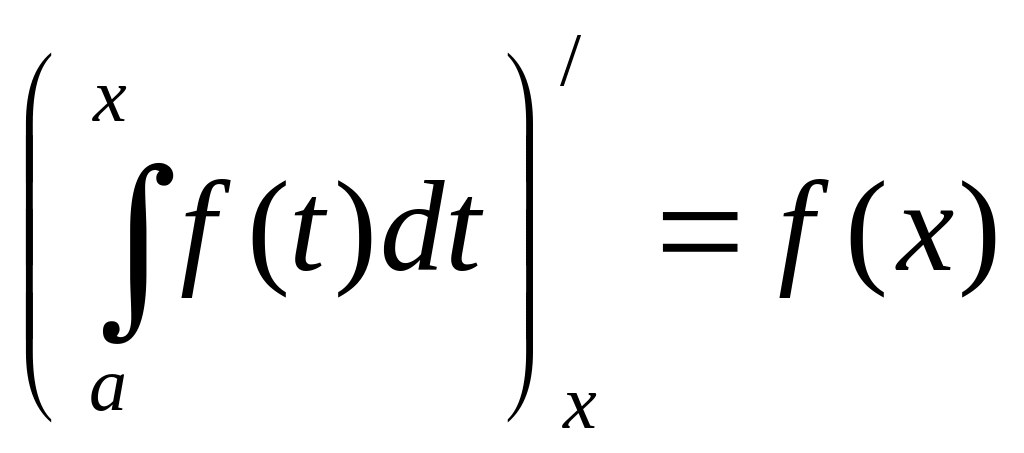 .
.
Док-во. По формуле
Ньютона-Лейбница имеем:
![]() .
Следовательно,
.
Следовательно,
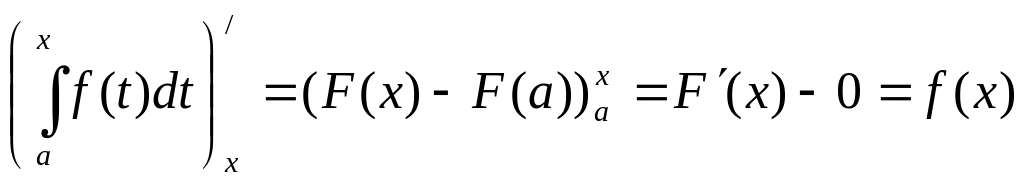 .
Это означает, что определенный интеграл
с переменным верхним пределом есть одна
из первообразных подынтегральной
функции.
.
Это означает, что определенный интеграл
с переменным верхним пределом есть одна
из первообразных подынтегральной
функции.
Необходимое условие интегрируемости. Если функция является интегрируемой на ограничена на .
Вычисления определенного интеграла: (на примерах)
Формула Ньютона-Лейбница..
Интегрирования подстановкой (заменой переменных).
Интегрирования по частям.
