9. Прямая и плоскость в пространстве, их уравнения. Взаимное расположение прямых и плоскостей.
Общее уравнение плоскости в пространстве.
Рассмотрим общее
уравнение первой степени с тремя
переменными
:
(1)
Это уравнение называется общим уравнением плоскости.
Частные случаи общего уравнения плоскости:
1. Если
,
то оно принимает вид
.
Этому уравнению удовлетворяет точка
.
В этом случае плоскость проходит через
начало координат.
2. Если
,
то
.
Плоскость будет параллельна оси
,
если
- параллельна оси
,
- параллельна оси
.
3. Если
,
то плоскость проходит через
параллельно оси
,
т.е. плоскость
проходит через ось
.
Аналогично, уравнениям
и
отвечают плоскости, проходящие
соответственно через оси
и
.
4. Если
,
то уравнение (1) принимает вид
,
т.е.
.
Плоскость параллельна плоскости
.
Аналогично,
и
.
5. Если
,
то уравнение (1) примет вид
,
т.е.
.
Это уравнение плоскости
.
Аналогично:
и
.
Каноническое уравнение прямой в пространстве.
Положение прямой
в пространстве вполне определено, если
задать какую-либо точку
на прямой и вектор
,
параллельный этой прямой. Вектор
называется направляющим вектором
прямой.
Пусть
- направляющий вектор прямой
и
- точка, лежащая на этой прямой. Вектор
,
соединяющий точку
с произвольной точкой
прямой
,
параллелен вектору
.
Поэтому координаты вектора
и вектора
пропорциональны:
.
(3) Уравнения (3) называются каноническими
уравнениями прямой в пространстве.
Прямая и плоскость в пространстве.
1. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.
Пусть плоскость
задана уравнением
,
а прямая
уравнениями
.
Углом между прямой и плоскостью называется
любой из двух смежных углов, образованных
прямой и проекцией на плоскость. Обозначим
через
угол между плоскостью
и прямой
,
а через
- угол между векторами
и
(см. рис.)
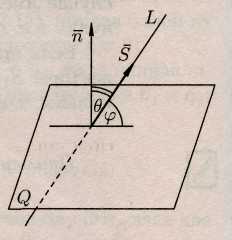
Тогда
.
Найдем синус угла
,
считая
:
.
И так как
,
получаем
. (4)
Если прямая
параллельна плоскости
,
то векторы
перпендикулярны (см. рис.)
,
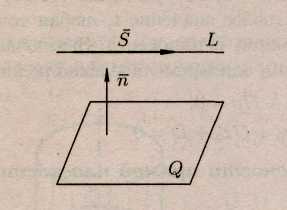а поэтому
,
т.е.
является условием
параллельности прямой и плоскости.
Если прямая
перпендикулярна плоскости
,
то векторы
параллельны (см. рис.)
.
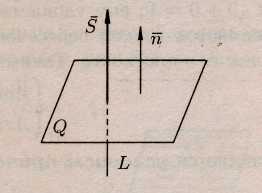Поэтому равенства
являются условиями
перпендикулярности прямой и плоскости.
2. Пересечение прямой с плоскостью. Условие принадлежности прямой плоскости.
Пусть требуется найти точку пересечения прямой (5) с плоскостью (6)
Для этого надо
решить систему уравнений (5) и (6). Проще
всего это сделать, записав уравнение
прямой (5) в параметрическом виде:
.
Подставляя эти выражения для
в уравнение плоскости (6), получаем
уравнение
или
(7)
Если прямая
не параллельна плоскости, т.е. если
,
то из равенства (7) находим значение
:
.
Подставляя найденное значение
в параметрические уравнения прямой,
найдем координаты точки пересечения
прямой с плоскостью.
Рассмотрим теперь
случай, когда
(
):
1. если
,
то прямая
параллельна плоскости и пересекать ее
не будет (уравнение (7) решения не имеет,
так как имеет вид
,
где
);
2. если
,
то уравнение (7) имеет вид
;
ему удовлетворяет значение
,
любая точка прямой является точкой
пересечения прямой и плоскости. Заключаем:
прямая лежит в плоскости. Такм образом,
одновременное выполнение равенств
является условием
принадлежности прямой плоскости.