Лемма о несамодвойственной функции

Если , то из неё путем подстановки и вместо переменных можно получить константу.

Доказательство:

Так как , то такой набор , что

Функцию (делаем замену )

Так как

Пример: Можно ли получить константу из функции

1)

		Замена: или
000	1
001	0
010	1
011	0
100	1
101	0
110	1
111	1

Лемма о немонотонной функции

Если функция не является монотонной, то из неё с помощью подстановки 0,1 и вместо переменных можно получить .

Доказательство:

Пусть , тогда и

наборы

функцию

Пример: Определить, можно ли получить функцию из функции:

1) , так как

Делаем замену:

, если

, если

так как

Проверять монотонность можно с помощью диаграммы:

1. Хассе

Пример:

(1,1)

(0,1) (1,0)

(0,0)

Если при движении по каждому ребру значение функции не уменьшается, то функция является монотонной.

Следовательно, не монотонна.

2. Разделим вектор 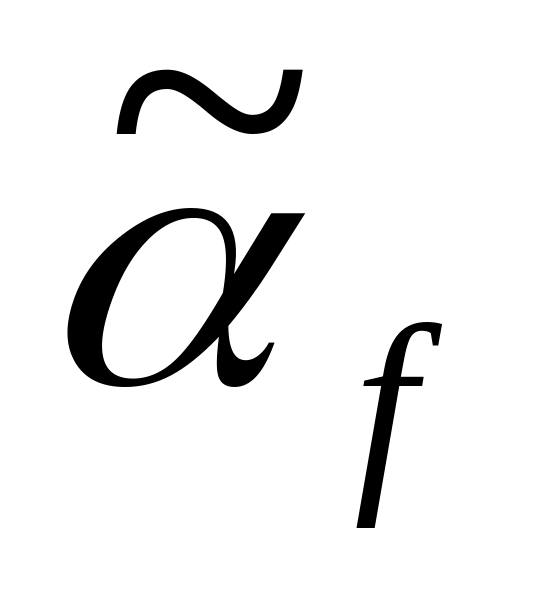не две равные части, если , то функция не является монотонной.

Если , то каждый из векторов вновь разделим на 2 равные части и так далее.

Если выполняется для всех пар, то .

Пример:

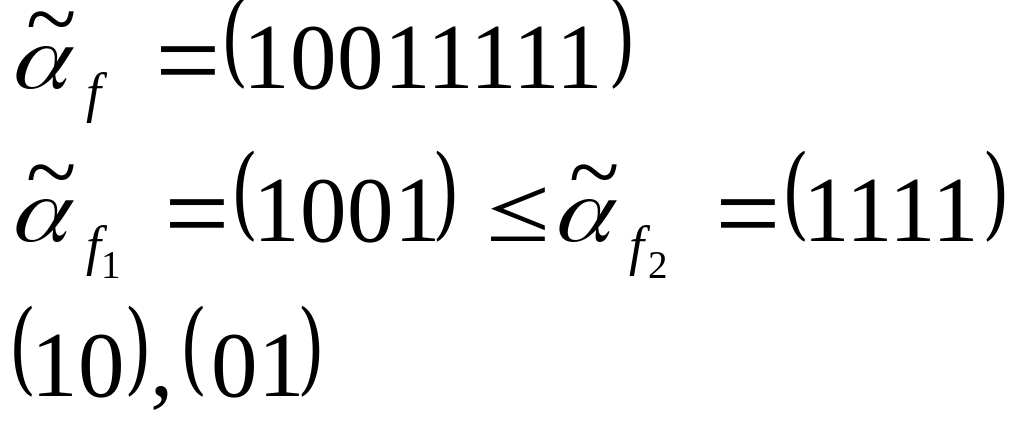
не сравнимы

функция не является монотонной.

Теорема: Класс замкнутый класс

Доказательство:

Пусть , функция не является линейной относительно и , тогда

где

Выберем такой набор , что

Подставим

Обозначим

Можно заметить, что

То есть

Пример: Выяснить является ли функция линейной, если нет, то построить

1)

с/р 2)

5. Класс класс линейных функций

Примеры:

Теорема: Класс замкнутый класса

Лемма о нелинейной функции

Если функция нелинейная, то из неё с помощью подстановки 0,1, а также и быть может навешивания отрицания над всей функцией можно получить конъюнкцию .

Система булевых функций является полной когда она целиком не содержится ни в одном из замкнутых классов: .

2 Достаточность

Пусть не содержится ни в одном из классов, тогда функции такие, что

Достаточно показать, что эта система является полной.

Для доказательства получим отрицание, константы, :

Возьмем , то есть

Функцию

Случай (а): получили , берем и по лемме 10 несом. функции получаем вторую константу. Таким образом, имеем систему по лемме 30 нелинейные функции, получаем .

Случай (б): , так как , то , то есть получены обе константы.

Берем функцию и получаем по лемме 0 немон. функции

получаем аналогично.

Таким образом мы выразили через функции , так как полная, то полная.

2)

с/р 3)

Все рассмотренные 5 классов не полные и попарно различны, то есть булевы функции, не принадлежащие ни одному из классов, и есть функции одному из любых 2-ух классов.