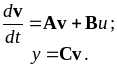4.3.3. Аналитическое конструирование регуляторов

Требования устойчивости и качества процессов можно описывать в неявной форме как экстремали тех или иных функционалов. Наиболее часто, в силу относительной простоты вычислений при достаточной физичности, применяют интегральные квадратичные функционалы (см.п.3.11.2). В случае, когда объект описан в форме пространства состояний, интегральный квадратичный функционал записывается в виде

,

(4.13)

где: v — вектор состояния; u — скалярное управление; Q — неотрицательно-определенная весовая матрица; r — весовой коэффициент. Безусловная экстремаль функционала (4.13) отвечает желаемому поведению и зависит от выбора весовых коэффициентов.

В п. 3.11.2 рассматривался вопрос о взаимосвязи интегральных и временных показателей качества. На примере улучшенной интегральной квадратичной оценки было показано, что большие значения коэффициента веса при производной процесса означают стремление к медленно затухающим экспоненциальным процессам с малыми значениями скоростей. Введение в функционал старших производных позволяет учесть большее разнообразие требований к протеканию процессов. Дополнение функционала членом означает косвенное ограничение энергии управления.

Задачей синтеза является определение матрицы коэффициентов обратной связи по состоянию K (см.п.4.3.2), доставляющей минимум функционалу (4.13). Минимизация (4.13) при динамических ограничениях в виде дифференциальных уравнений объекта (4.8) дает условную экстремаль.

Оказывается [ ], что матрица K коэффициентов обратных связей находится из соотношения

,

где матрица является решением нелинейного матричного уравнения Риккати (Riccati)

.

(4.14)

Уравнения такого вида решаются численно.

Рассмотрим пример стабилизации перевернутого маятника, заданного уравнениями состояний (4.8) с матрицами (4.12). Примем весовую матрицу Q в функционале (4.13) единичной; положим также . В результате проведения необходимых вычислений, включающих решение уравнения Риккати, получаем матрицу обратных связей:

.

При этом собственные значения матрицы замкнутой системы получаются следующими: .

Поскольку при значительной исходной неопределенности трудно сразу выбрать весовые коэффициенты функционала I, то задача решается путем последовательных приближений.

Изменим весовой коэффициент r функционала (4.13) при управлении, приняв . Соответствующая матрица обратных связей будет равна:

,

а собственные значения матрицы замкнутой системы получатся следующими: .

4.3.4. Синтез наблюдателя состояний

При построении регуляторов в п.4.3.3 предполагалось, что все переменные состояния объекта управления могут быть измерены непосредственно. Однако, как правило, измеряются только переменные выхода, число которых меньше порядка модели объекта. Уравнения состояния (4.8) в этом случае дополняются уравнением выхода:

(4.15)

Если объект наблюдаем полностью, то по измеренным значениям переменной выхода y можно вычислять текущее состояние объекта. При этом управляющее воздействие на объект формируется по оценкам вектора состояния

.

Наблюдатель состояния представляет собой модель объекта, охваченную обратной связью по отклонению выходов модели и объекта y (рис.4.9).

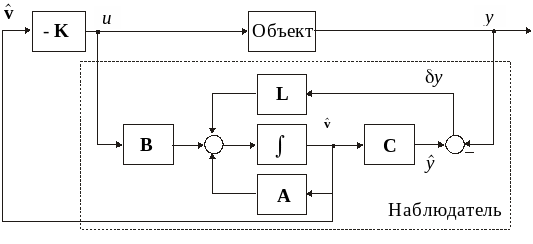Рис. 4.9. Наблюдатель состояния

Оценка вектора состояния отличается от состояния v объекта из-за различия начальных условий, действующих на объект возмущений, а также неточности описания объекта. Однако при правильном выборе матрицы обратной связи наблюдателя L оценка должна асимптотически стремиться к состоянию объекта.

Можно показать, что задача синтеза наблюдателя — определения матрицы L — является дуальной по отношению к задаче синтеза регулятора — определения матрицы (см.п.4.3.2, 4.3.3). Поэтому матрицу наблюдателя можно найти теми же методами, если вместо пары матриц принять пару . При назначении желаемых собственных значений матрицы или весовых коэффициентов функционалов вида (4.13) необходимо стремиться к большему быстродействию контура наблюдателя.

Рассмотрим пример синтеза наблюдателя для перевернутого маятника. Пусть измеряется положение маятника y. Тогда, в силу выбора переменных состояния: , матрица выхода .

Проведем синтез методом размещения корней. Назначим собственные значения наблюдателя значительно дальше от мнимой оси, чем собственные значения системы, т.е. примем: . Получим следующую матрицу наблюдателя .

Наблюдатель вместе с регулятором состояния образуют динамический регулятор, входом которого является выход объекта, а выходом — управляющее воздействие на объект (см.рис.4.9). Передаточная функция этого регулятора для рассматриваемого примера равна:

.

Оказалось, что нуль передаточной функции регулятора равен левому, оставляемому на месте, полюсу передаточной функции объекта. Корни характеристического полинома замкнутой системы

в точности равны назначенным корням системы: и наблюдателя .

Отметим в заключение, что недостатком синтезированного наблюдателя является его избыточность. Поскольку одна из переменных состояния измеряется, то следует синтезировать наблюдатель, порядок которого меньше порядка модели объекта [ ].