4.3. Стабилизация неустойчивых объектов

Пусть анализ линейной модели, описывающей движения объекта в окрестности выбранного режима работы, показал, что режим неустойчив. Математически этот факт выражается в том, что характеристический полином дифференциального уравнения имеет корни с неотрицательными действительными частями. Возникает задача стабилизации неустойчивого объекта. В других случаях объект может быть устойчивым, но его собственные движения не удовлетворяют требованиям, например, сильно колебательные или/и затухают слишком медленно.

Необходимым топологичесим условием изменения расположения корней характеристического полинома является образование контура, содержащего объект управления (см.п.3.3.2). Кроме того, передаточная функция объекта по выбранному каналу вход-выход не должна иметь неустойчивых диполей. В противном случае никакая обратная связь не сможет переместить корни неполной части.

В зависимости от формы представления модели объекта и требований к собственным движениям системы могут быть применены различные методы синтеза.

4.3.1. Размещение корней характеристического полинома. Операторный метод

Допустим, что требования к системе представлены в форме желаемого множества корней характеристического полинома. Необходимо найти алгоритм регулятора, размещающего корни в назначенных местах комплексной плоскости. Корни характеристического полинома — это полюсы передаточной функции системы; по этой причине иногда говорят о задаче размещения полюсов. Поскольку корням соответствуют составляющие собственных движений  — так называемые моды — то задачу размещения корней иногда называют управлением модами или модальным управлением.

Запишем дифференциальное уравнение объекта в операторной форме

.

(4.1)

Положим, что степень полинома выше степени полинома . Кроме того, допустим, что полиномы и взаимно просты, т.е. описание вход-выход объекта (4.1) является полным (см.подразд.2.4).

Без потери общности примем, что коэффициент при старшей степени полинома равен единице.

Искомое дифференциальное уравнение стабилизирующей отрицательной обратной связи (регулятора ) также запишем в общем виде в операторной форме

.

(4.2)

Однородное дифференциальное уравнение автономной замкнутой системы получим, если исключим переменную из уравнений (4.1) и (4.2):

.

(4.3)

Потребуем тождества характеристического полинома желаемому полиному

,

(4.4)

построенному по заданным корням

.

(4.5)

Из тождества (4.5) необходимо найти операторные полиномы регулятора и . Это значит, что следует искать структуру регулятора — степени и , а также параметры регулятора — коэффициенты полиномов:

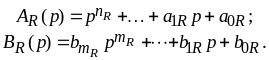
Полиномиальные уравнения вида (4.5) называют диофантовыми, так как полиномы, как и целые числа, образуют кольцо — алгебраическую структуру с операциями сложения, вычитания и умножения (без деления).

Для конкретизации структуры регулятора воспользуемся условием реализуемости регулятора:

;

(4.6)

для упрощения задачи примем степени равными: . Тогда число неизвестных параметров регулятора равно .

Из условия равенства коэффициентов полиномов и имеем систему уравнений для определения коэффициентов полиномов и .

Степень полинома равна сумме степеней полиномов и , т.е. порядок системы равен сумме порядков объекта и регулятора. Такой же должна быть и степень желаемого характеристического полинома . В силу того, что полиномы и имеют единичные старшие коэффициенты, а степень полинома меньше степени полинома , старший коэффициент полинома также равен единице. Как видно из (4.4), полином имеет единичный старший коэффициент. Таким образом, из тождества (4.5) следует уравнений.

Число неизвестных параметров должно равняться числу уравнений:

;

откуда получим порядок регулятора:

.

(4.7)

Порядок системы равен

;

таково же и число неизвестных параметров регулятора.

Далее записывается система уравнений относительно искомых параметров. Матрица системы формируется из коэффициентов полиномов и ; она оказывается так называемой матрицей Сильвестра (Sylvester). Ее определитель — результант полиномов и  — отличен от нуля, если полиномы взаимно просты. Таким образом, задача размещения корней разрешима, если характеристика вход-выход объекта является полной.

Рассмотрим пример стабилизации маятника (см. рис.1.7, а) в верхнем положении равновесия. Пусть масса m сосредоточена в точке, трение и сопротивление среды отсутствуют. Малые отклонения маятника от верхнего положения равновесия описываются дифференциальным уравнением второго порядка

,

где: u — управляющее воздействие. Для простоты принято, что значение l — длины маятника численно равно значению g — ускорения силы тяжести.

Один из корней характеристического полинома дифференциального уравнения объекта положителен. Действительно, верхнее положение маятника не устойчиво.

Поскольку порядок объекта равняется двум, то из (4.7) найдем порядок (структуру) регулятора: . Следовательно, необходимо определить три коэффициента дифференциального уравнения регулятора

.

Порядок системы равен трем; назначим три желаемых корня: и сформируем в соответствии с выражением (4.4) желаемый характеристический полином:

.

Один из корней характеристического полинома объекта (левый) оставляем на месте. Характеристический полином замкнутой системы в соответствии с уравнением (4.3) для данного примера имеет вид:

.

Из тождества и получим систему уравнений

решая которую получим искомые коэффициенты регулятора, обеспечивающего заданное расположение корней:

Передаточная функция разомкнутого контура стабилизации

имеет диполь , равный оставляемому на месте корню объекта.

На рис.4.5 изображена ЛАЧХ контура (кривая 1). Частота среза системы 2c^-1.

Рис.4.5. ЛАЧХ к примеру решения задачи стабилизации операторным методом

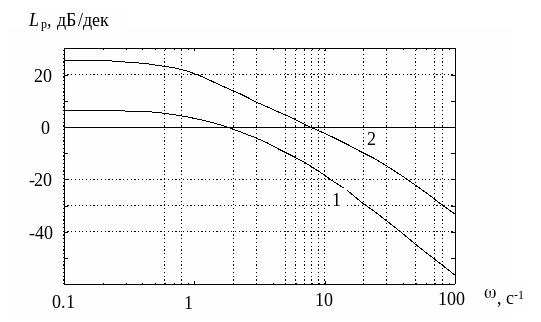
Изменим положение желаемых корней системы:

. Удаление корней от мнимой оси отражает стремление к повышению быстродействия системы. При этом получим следующую передаточную функцию регулятора

.

На рис.4.5 (кривая 2) изображена ЛАЧХ разомкнутого контура соответствующей системы. Наблюдаем расширение полосы частот; частота среза 9с^-1 .

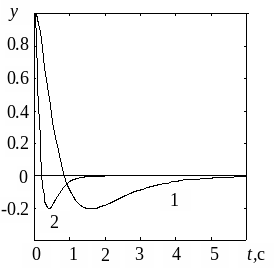
На рис.4.6, а приведены графики процессов в первой и второй системах при следующих начальных условиях: Видно, что во второй системе процесс затухает быстрее — маятник быстрее возвращается в положение равновесия. Длительность процессов: 1.25с; 5с . На рис.4.6, б изображены графики изменения управляющих воздействий ; во второй системе уровни воздействий на объект гораздо выше: 20

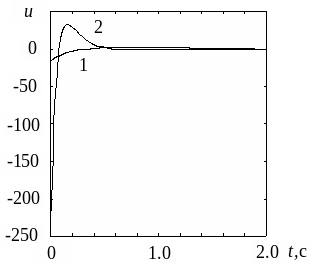
а б

Рис. 4.6. Графики процессов к примеру решения задачи стабилизации операторным методом

Описанная процедура решения задачи стабилизации является простейшей; она может быть усовершенствована.

Подбором полиномов и можно получить любой желаемый характеристический полином системы и даже добиться понижения степени за счет взаимного уничтожения старших коэффициентов. При этом часть корней полинома уходит в бесконечность. Поскольку неточная компенсация может дать полиномы с малыми отрицательными коэффициентами, то часть корней переходит в правую полуплоскость. Системы, полученные таким образом, оказываются негрубыми — при малейшей неточности в реализации регулятора или несоответствии объекта модели система будет катастрофически неустойчивой — характеристический полином будет иметь большие по модулю правые корни.