
- •3. Анализ систем управления
- •3.1. Задачи анализа
- •3.2. Анализ устойчивости
- •3.2.1. Свободные движения
- •3.2.2. Условие устойчивости
- •3.2.3. Устойчивость вход-выход
- •3.3. Критерии устойчивости
- •3.3.1. Необходимое условие устойчивости
- •3.3.2. Алгебраические критерии
- •3.3.3. Критерий Михайлова
- •3.4. Устойчивость систем с типовой структурой
- •3.4.1. Устойчивость систем без контуров
- •3.4.2. Устойчивость одноконтурных систем
- •3.5. Критерий Найквиста
3.3.3. Критерий Михайлова
Критерий Михайлова относят к частотным
критериям. Он базируется на принципе
аргумента [50]. Выражение для
характеристического полинома
![]() рассматривается как функция комплексного
переменного, принимающего значения на
положительной мнимой полуоси. Критерий
сводится к анализу изменения аргумента
функции
рассматривается как функция комплексного
переменного, принимающего значения на
положительной мнимой полуоси. Критерий
сводится к анализу изменения аргумента
функции
![]() .
.
Согласно критерию Михайлова для устойчивости системы необходимо и достаточно, чтобы годограф вектора , начинаясь при = 0 на действительной положительной полуоси, с ростом от нуля до бесконечности обходил последовательно в положительном направлении (против часовой стрелки) n квадрантов, где n — порядок системы:
![]()
3.4. Устойчивость систем с типовой структурой
Рассмотрим системы, образованные последовательным и параллельным соединениями звеньев, а также системы с обратной связью.
Будем иметь в виду асимптотическую
устойчивость по начальному состоянию,
которая устанавливается по модели
собственно системы
![]() .
.
3.4.1. Устойчивость систем без контуров
Как показано в 2.10, характеристический полином системы в случае последовательного и параллельного соединений звеньев равен произведению характеристических полиномов звеньев
![]() .
.
Отсюда следует вывод: необходимым и достаточным условием устойчивости системы, образованной последовательным и параллельным соединениями звеньев, является устойчивость всех звеньев. Вывод сохраняет силу при любом числе звеньев, включенных параллельно и последовательно, т. е. для любых бесконтурных графов.
3.4.2. Устойчивость одноконтурных систем
Характеристический полином замкнутой системы, образованной соединением звеньев с обратной связью (см. рис. 2.9, в),
![]() .
.
Для одноконтурных систем, образованных любым числом звеньев с передаточными функциями
![]() ,
,
характеристический полином записывается как сумма
|
(3.6) |
полиномов знаменателя и числителя передаточной функции разомкнутой системы
![]() .
.
О расположении корней полинома (3.6),
полученного суммированием двух полиномов,
в общем случае без предварительных
вычислений ничего сказать нельзя.
Необходимо либо вычислить корни
![]() ,
либо применить какой-либо критерий
устойчивости. Вместе с тем следует
указать на два важных случая.
,
либо применить какой-либо критерий
устойчивости. Вместе с тем следует
указать на два важных случая.
Если полиномы
![]() и
и
![]() имеют нетривиальный общий делитель —
полином
имеют нетривиальный общий делитель —
полином
![]() ,
т.е. передаточная функция разомкнутой
системы
,
т.е. передаточная функция разомкнутой
системы
![]() имеет диполи, то при замыкании системы
соответствующие корни характеристического
полинома не перемещаются. Действительно,
из выражения
имеет диполи, то при замыкании системы
соответствующие корни характеристического
полинома не перемещаются. Действительно,
из выражения
![]()
следует, что корни полинома
являются и корнями полинома
![]() .
Таким образом, необходимое условие
устойчивости замкнутой системы —
все корни наибольшего общего делителя
.
Таким образом, необходимое условие
устойчивости замкнутой системы —
все корни наибольшего общего делителя
![]()
левые. Достаточное условие неустойчивости — наличие у полиномов и общего делителя с правым корнем.
Как показано в 2.4, наличие общих корней у полиномов числителя и знаменателя передаточной функции соответствует неполной системе. При замыкании такой системы неполная часть своих свойств не изменяет.
непосредственно неизмеряемым возмущениям.
3.5. Критерий Найквиста
Критерий Найквиста является необходимым и достаточным условием устойчивости систем с обратной связью.
Рассмотрим одноконтурную систему с
передаточной функцией разомкнутого
контура
![]() .
Рациональная функция
.
Рациональная функция
![]()
называется возвратной разностью. Скажем также, что это определитель одноконтурного графа с отрицательной обратной связью.
Возвратная разность равна отношению характеристических полиномов замкнутой и разомкнутой систем
![]() .
.
Будем рассматривать
![]() как функцию комплексного аргумента.
как функцию комплексного аргумента.
Критерий Найквиста базируется на
принципе аргумента [ ]. Пусть C —
произвольный замкнутый контур без
самопересечений на плоскости s, а
—
рациональная функция s, не имеющая
на контуре C ни нулей, ни полюсов.
Разность
![]() между количеством нулей и полюсов
однозначной функции
,
заключенных внутри замкнутой кривой
C, равна числу полных оборотов,
которые делает вокруг начала координат
вектор
,
в то время как точка s описывает
контур C по часовой стрелке. При
исследовании асимптотической устойчивости
в качестве контура C выбирается
мнимая ось и полуокружность бесконечного
радиуса (контур Найквиста охватывает
правую полуплоскость).
между количеством нулей и полюсов
однозначной функции
,
заключенных внутри замкнутой кривой
C, равна числу полных оборотов,
которые делает вокруг начала координат
вектор
,
в то время как точка s описывает
контур C по часовой стрелке. При
исследовании асимптотической устойчивости
в качестве контура C выбирается
мнимая ось и полуокружность бесконечного
радиуса (контур Найквиста охватывает
правую полуплоскость).
Нулями
являются корни характеристического
полинома замкнутой системы, а полюсами —
корни характеристического полинома
разомкнутой системы. Если
![]() ,
т.е. разомкнутая система устойчива, то
для устойчивости замкнутой системы
,
т.е. разомкнутая система устойчива, то
для устойчивости замкнутой системы
![]() необходимо и достаточно, чтобы кривая
при движении s вдоль C по часовой
стрелке не охватывала начала координат.
необходимо и достаточно, чтобы кривая
при движении s вдоль C по часовой
стрелке не охватывала начала координат.
Вместо возвратной разности можно рассматривать возвратное отношение — передаточную функцию разомкнутой системы
![]() .
.
При этом для устойчивости замкнутой
системы необходимо и достаточно, чтобы
годограф
—
амплитудно-фазовая характеристика
разомкнутой системы — при движении
s вдоль C по часовой стрелке не
охватывал точку
![]() .
.
На рис. 3.6, а изображен случай
устойчивой замкнутой системы, которая
устойчива и в разомкнутом состоянии.
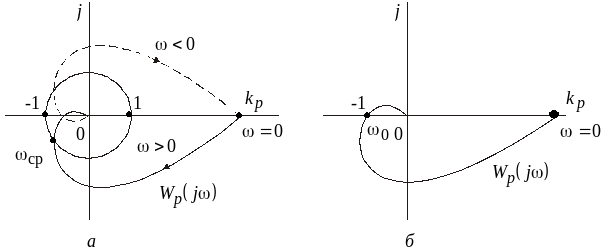
Рис. 3.6. Иллюстрация критерия Найквиста
Если амплитудно-фазовая характеристика
устойчивой разомкнутой системы проходит
через критическую точку
на частоте
![]() ,
то пара корней характеристического
полинома замкнутой системы окажутся
чисто мнимыми
,
то пара корней характеристического
полинома замкнутой системы окажутся
чисто мнимыми
![]() .
Этот случай называют колебательной
границей устойчивости (рис. 3.6, б).
.
Этот случай называют колебательной
границей устойчивости (рис. 3.6, б).
Рациональные функции
и
имеют одни и те же полюсы. Если среди
них имеется p правых полюсов, т.е.
разомкнутая система является неустойчивой,
для устойчивости замкнутой системы
амплитудно-фазовая характеристика
![]() должна p раз охватывать точку
против часовой стрелки. В силу
симметричности характеристик:
должна p раз охватывать точку
против часовой стрелки. В силу
симметричности характеристик:
![]()
можно ограничиться рассмотрением
![]() т.е. половины контура C на комплексной
плоскости. Соответственно изменится и
формулировка критерия Найквиста.
т.е. половины контура C на комплексной
плоскости. Соответственно изменится и
формулировка критерия Найквиста.
Для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика p/2 раз охватывала точку против часовой стрелки, где p — число правых корней характеристического полинома разомкнутой системы (правых полюсов передаточной функции разомкнутой системы).
Очевидно, выполнение достаточного условия устойчивости (3.9) гарантирует, что амплитудно-фазовая характеристика (см.рис.3.4) не охватывает точку . Вместе с тем ясно, что необходимое и достаточное условие Найквиста оставляет большую свободу для формирования при условии устойчивости замкнутой системы.
Пусть для примера передаточная функция разомкнутой системы имеет вид
![]() ,
,
т. е. имеет один правый полюс. Разомкнутая
система неустойчива. Для устойчивости
замкнутой системы амплитудно-фазовая
характеристика
при
изменении от нуля
до бесконечности должна 1/2 раза охватить
точку
против часовой стрелки. Как видно из
рис.3.7, это возможно при k > 1 (замкнутая
система устойчива при
![]() и неустойчива при
и неустойчива при
![]() ).
Для перемещения корня из правой
полуплоскости в левую необходимо
достаточно большое усиление контура.
).
Для перемещения корня из правой
полуплоскости в левую необходимо
достаточно большое усиление контура.
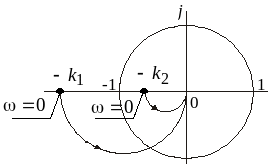
Рис. 3.7. Пример применения критерия Найквиста
Передаточную функцию разомкнутой системы во многих случаях удобно представлять в следующем виде:
![]() ,
,
где
![]() — коэффициент
передачи разомкнутой системы. Он равен
отношению младших отличных от нуля
коэффициентов полиномов числителя и
знаменателя. Передаточную функцию
— коэффициент
передачи разомкнутой системы. Он равен
отношению младших отличных от нуля
коэффициентов полиномов числителя и
знаменателя. Передаточную функцию
![]() назовем нормированной. В частном случае
ненулевых нулей и полюсов
назовем нормированной. В частном случае
ненулевых нулей и полюсов
![]()
является коэффициентом усиления; он характеризует свойства контура по постоянному сигналу.
Рассмотрим рациональную функцию
![]() ,
,
числитель которой есть характеристический
полином замкнутой системы. Для устойчивости
замкнутой системы
нормированная амплитудно-фазовая
характеристика
![]() должна p/2 раз охватывать точку
должна p/2 раз охватывать точку
![]() против часовой стрелки.
против часовой стрелки.
Такая формулировка критерия Найквиста
упрощает исследование зависимости
устойчивости замкнутой системы от
коэффициента передачи контура. При
изменении
нормированная амплитудно-фазовая
характеристика не изменяется, а
критическая точка
превращается в критический отрезок
(луч), как это показано на рис.3.8. Здесь
легко найти критический коэффициент
усиления — он соответствует точке
пересечения амплитудно-фазовой
характеристики
![]() с критическим отрезком.
с критическим отрезком.
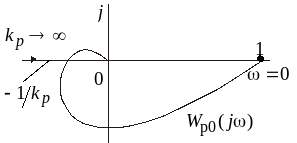 Рис. 3.8.
Применение критерия Найквиста для
нормированных характеристик
Рис. 3.8.
Применение критерия Найквиста для
нормированных характеристик
Если передаточная функция разомкнутой системы имеет полюсы на мнимой оси (остальные левые) — нулевой полюс в случае интегратора в составе звеньев или пару мнимых полюсов консервативного звена, то выбор контура C имеет свою специфику. Чтобы принять число корней p разомкнутой системы внутри контура C равным нулю и сохранить формулировку критерия, этот контур обходит полюсы на мнимой оси по полуокружностям бесконечно малого радиуса.
Амплитудно-фазовая характеристика
при значениях, близких к полюсам на
мнимой оси, а именно, при их обходе против
часовой стрелки по дугам окружности
малого радиуса, принимает по модулю
бесконечно большое значение; аргумент
амплитудно-фазовой характеристики
изменяется на
![]() по часовой стрелке. Если
по часовой стрелке. Если
![]() ,
то в случае нулевого полюса аргумент
изменяется при = 0
на -/2. На рис.3.9, а
в качестве примера качественно изображена
амплитудно-фазовая характеристика для
передаточной функции:
,
то в случае нулевого полюса аргумент
изменяется при = 0
на -/2. На рис.3.9, а
в качестве примера качественно изображена
амплитудно-фазовая характеристика для
передаточной функции:
![]() ,
,
а на рис.3.9, б — для
![]() .
.
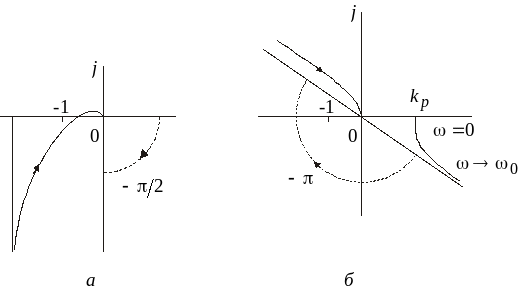 Рис. 3.9.
Примеры амплитудно-фазовых характеристик
для критических случаев
Рис. 3.9.
Примеры амплитудно-фазовых характеристик
для критических случаев
В случае систем высокого порядка амплитудно-фазовая характеристика может иметь сложный вид, затрудняющий подсчет числа охватов критической точки. Для упрощения рекомендуется считать число переходов амплитудно-фазовой характеристики через луч (-, -1). Переход снизу вверх считается отрицательным, а сверху вниз — положительным. Для устойчивости замкнутой системы необходимо и достаточно, чтобы сумма переходов через луч равнялась +p/2, где p — число правых полюсов передаточной функции разомкнутой системы.
Особенно удобно применение критерия Найквиста, а также выявление влияния свойств звеньев на устойчивость, если строятся логарифмические частотные характеристики:
![]() .
.
Если передаточная функция разомкнутой
системы имеет p правых полюсов, для
устойчивости замкнутой системы необходимо
и достаточно, чтобы в интервале частот,
где
![]() число переходов
число переходов
![]() через линию -
равнялось p/2.
через линию -
равнялось p/2.
Положительным считается переход снизу вверх, а отрицательным — сверху вниз.
На рис.3.10, а изображены логарифмические частотные характеристики, а на рис.3.10. б — амплитудно-фазовая характеристика так называемой условно-устойчивой системы.
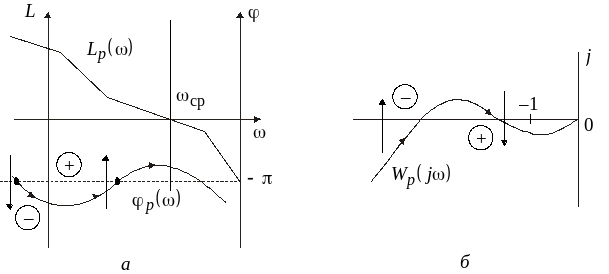 Рис. 3.10.
Характеристики условно-устойчивой
системы
Рис. 3.10.
Характеристики условно-устойчивой
системы
Критерий Найквиста можно применить только в том случае, когда выполняется необходимое условие устойчивости — неполная часть системы устойчива (диполи передаточной функции левые).
Критерий Найквиста физичен. Хорошо видна роль амплитудных и фазовых преобразований, вносимых контуром, на устойчивость системы в целом. Изначальный смысл применения критерия Найквиста заключается не столько в констатации устойчивости, сколько в выявлении роли контура в перемещении корней характеристического полинома системы. На базе этого критерия можно судить о влиянии свойств элементов на характер свободных движений системы в целом.
Практически важное свойство критерия Найквиста заключается также в том, что по нему можно исследовать устойчивость систем с обратными связями на основе экспериментально снятых частотных характеристик звеньев, образующих контур.
