58. Метод исключения для линейных систем с постоянными коэффициентами произвольного вида.

Рассмотрим систему вида: (4)

где M_ik(D) – операторные многочлены некоторой степени, f₁(x), f₂(x), …, f_n(x) – достаточное число раз дифференцируемые функции.Попытаемся получить дифференциальное уравнение для одной из неизвестных, например y₁. Подействуем на первое уравнение слева оператором N₁₁(D) – алгебраическим дополнением для элемента M₁₁(D) следующего операторного определителя

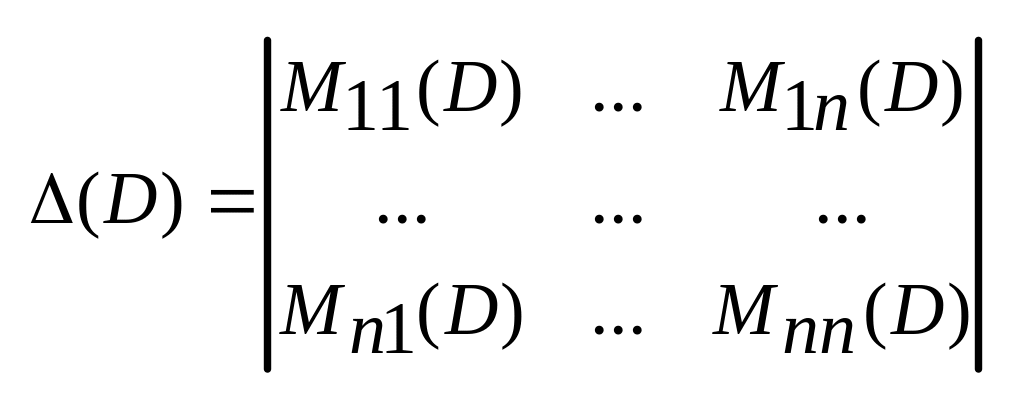(5).

На второе уравнение системы (4) подействуем слева оператором N₂₁(D) – алгебраическим дополнением для элемента M₂₁(D) определителя и т.д. На последнее уравнение действуем слева оператором N_n1(D) – алгебраическим дополнением для элемента M_n1(D) определителя (5). Затем, складывая получившиеся уравнения, получаем:

или

(6)

Уравнение (6) – линейное неоднородное уравнение с постоянными коэффициентами. Аналогичным образом получаются уравнения для определения неизвестных y₂, y₃, …, y_n:

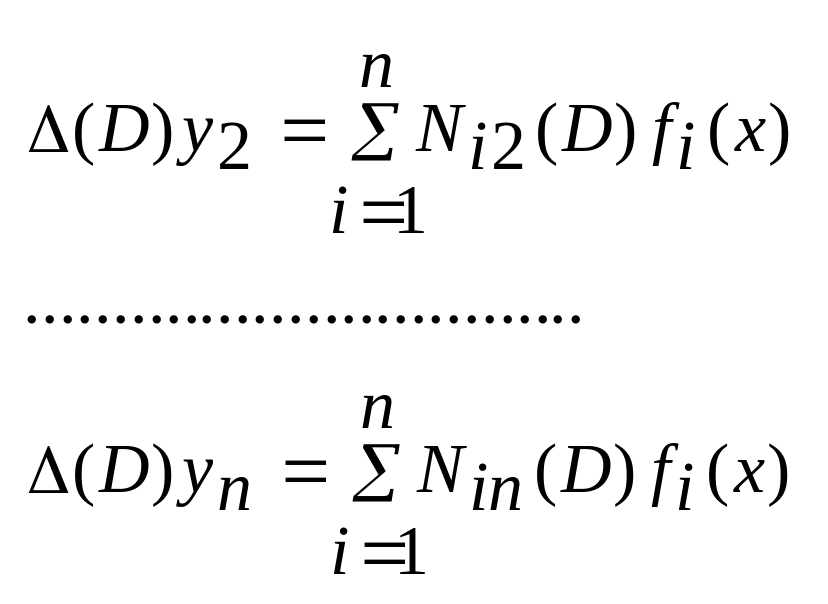(7)

При выводе системы (6)-(7) мы предполагали дифференцируемость решений. Этот факт можно доказать. Может также оказаться , тогда предложенный метод решения ничего не дает.

Пусть . Тогда определитель представляет собой операторный многочлен относительно D некоторой степени m. Степень многочлена m и называется порядком системы (4). Общее решение первого уравнения системы (6)-(7) будет содержать m произвольных постоянных, второго также m постоянных и т.д.Т.о., общее число произвольных постоянных окажется равным m*n. В соответствии с порядком системы (4) независимыми являются только m произвольных постоянных. Для того, чтобы установить зависимость между произвольными постоянными, следует найденные общие решения системы (6)-(7) подставить в исходную систему (4) и потребовать выполнения тождеств для любых x. В рез. этой процедуры должно остаться m произвольных постоянных, через которые выражаются все остальные.

59. Устойчивость по Ляпунову. Теорема Ляпунова об устойчивости и асимптотической устойчивости.

Рассмотрим систему дифференциальных уравнений:

(1)

Причем (2)

Опр: Решение системы (1) называется устойчивым по Ляпунову, если выполняется, что

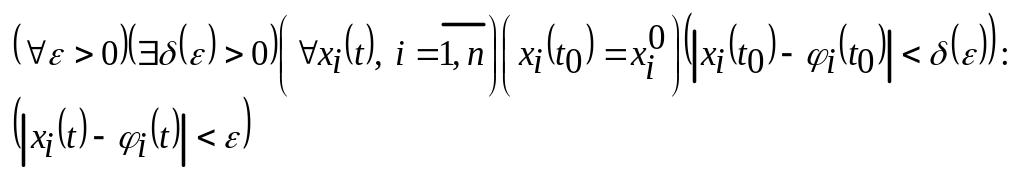(3).

Близкие по начальным условиям решения, остаются близкими и при .

Если система (1) удовлетворяет условию теоремы о непрерывной зависимости решений от начальных условий, то вместо следует писать .

Если ни при каком неравенство (3) не выполняется для , то -неустойчивое решение системы.

Решение задачи об устойчивости решения может быть сведено к исследованию на устойчивость нулевого решения:

(4)

(5)

-точка покоя.

Тривиальное решение (точка покоя) в (5) будет устойчивым по Ляпунову (в смысле Ляпунова), если для каждого для .

Иначе устойчива в смысле Ляпунова если:

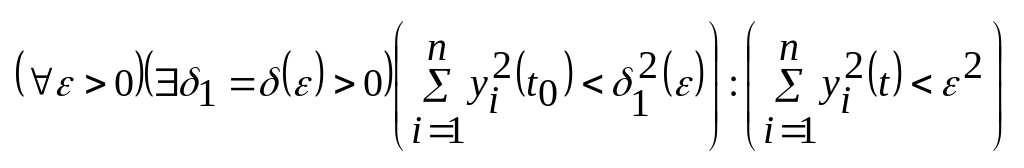для .

Траектория, начальная точка которой находится в окрестности начала координат, при не выходит за окрестность начала координат.

Теорема Ляпунова

Пусть дана система (1), имеющая тривиальное решение . Пусть существует дифференцируемая функция , удовлетворяющая условиям:

1)

2) Полная производная V вдоль решения системы (1) неположительная, т.е.

Тогда точка покоя устойчива по Ляпунову. Если дополнительно известно, что в сколь угодно малой окрестности начала координат ,где , то точка покоя асимптотически устойчива.

-функция Ляпунова.

(теорема принимается без доказательства)

Пример

x=0,y=0-решение

Рассмотрим

1)

2)

где -минимум функции вне круга

Функция Ляпунова ищется в квадратичной форме:

Рассмотрим систему:

(7)-автономная система

Точка , в которой правые части системы (1) обращаются в нуль, наз-ся точкой покоя или точкой равновесия системы

Точка покоя системы (7) будет особой точкой для системы симметричной (**).

№56 Линейные однородные системы с постоянными коэффициентами.

Рассмотрим линейную однородную систему уравнений с постоянными коэффициентами:

, (1)

где А – (n*n) матрица постоянных коэффициентов

.

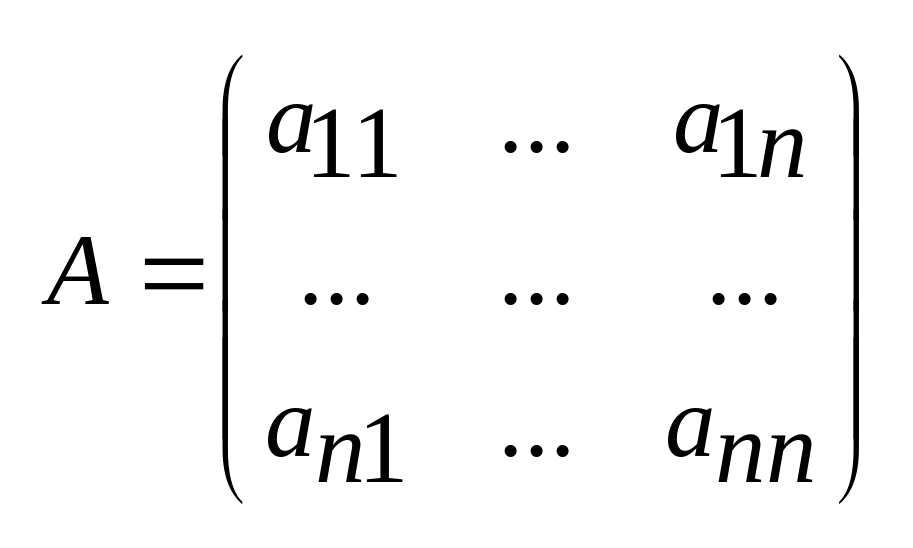Система (1) удовлетворяет теореме существования во всём пространстве E_n+1. Данную систему можно свести к линейному однородному уравнению n-го порядка для одной из переменных y_k, решение которого ищется в виде y_k=_ke^x. Исходя из этого будем искать нетривиальное решение однородной системы (1) в форме следующей вектор-функции

(2)

где - неизвестный постоянный вектор,  - неизвестная константа.

Подставляя (2) в (1), придём к

или

(3)

где Е={_ij} – единичная матрица. Однородная система (3) имеет ненулевое решение, когда

det(A-E)=0

или

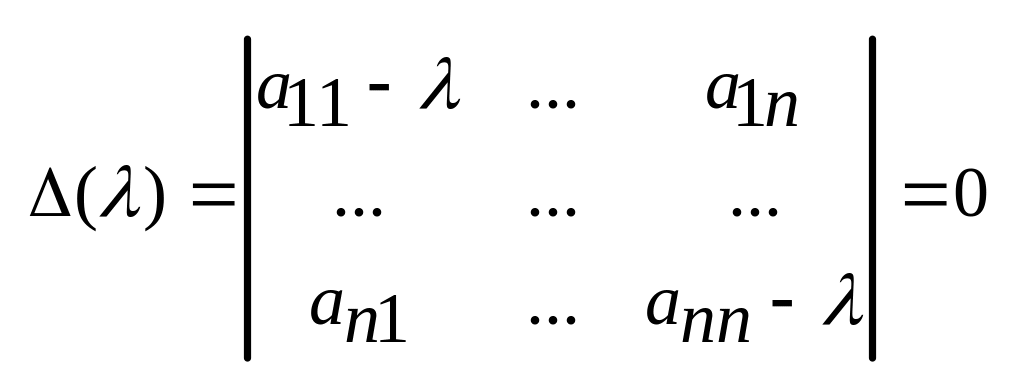(4)

Соотношение (4) представляет собой характеристическое уравнение для определения . Если раскрыть определитель, то левая часть (4) окажется многочленом n-ой степени по , который называют характеристическим.

Пусть все корни характеристического уравнения (4) простые: ₁, ₂,…, _n. В этом случае характеристический многочлен () допускает представление в виде:

()=(-_k) ₁(), (5)

причём ₁(_k)0. Из (5) следует, что

’()=₁()+(-_k) ₁’(),

и поэтому ’(_k)= ₁(_k)0. С другой стороны, по правилам дифференцирования функционального определителя

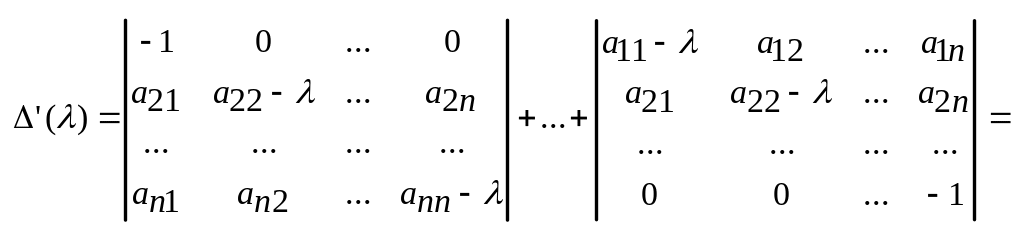
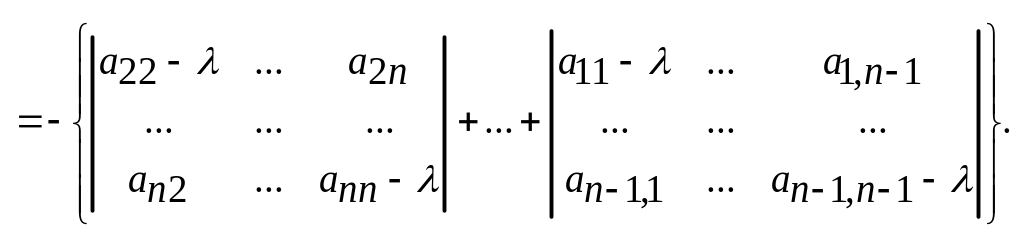
Поскольку сумма диагональных миноров (n-1) порядка матрицы

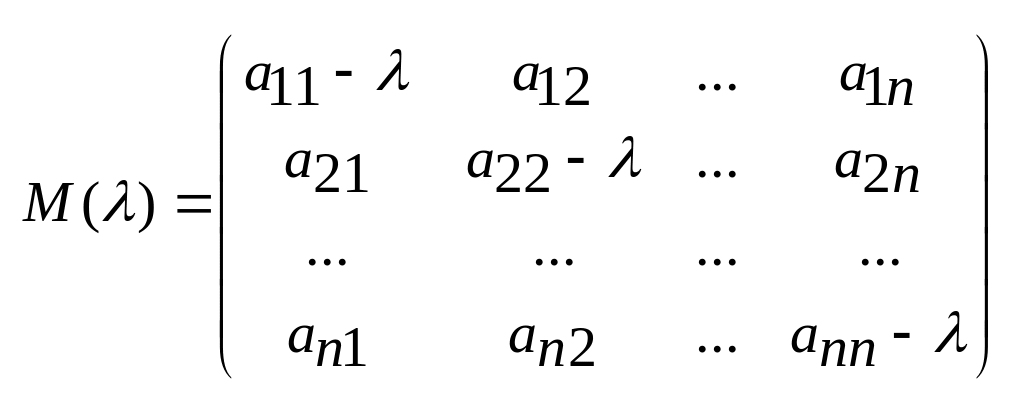
при =_k не обращается в нуль, то найдётся по крайней мере один из диагональных миноров, отличный от нуля. Это означает, что матрица M(_k) имеет rangM(_k)=r=n-1.

Для определения векторов будем последовательно подставлять в уравнение (3) =₁, =₂,…,=_n. В результате придём к уравнениям вида

или

(6)

Всего таких систем уравнений будет n, поскольку индекс k пробегает значения от 1 до n. Поскольку ранг матрицы M(_k): r=n-1, то компоненты собственных векторов определяются с точностью до произвольного множителя.

В качестве ненулевого решения системы уравнений (6) можно взять алгебраические дополнения элементов той строки матрицы M(_k), которые не обращаются в нуль. Такие миноры существуют ибо r=n-1. В результате найдём n решений однородной системы (1):

, k=1, 2,…,n (7)

Теперь необходимо доказать их линейную независимость.

Доказательство проведём методом «от противного». Пусть найденная система решений линейно зависима, т.е. найдутся ненулевые действительные постоянные ₁, ₂,…,_n (₁²+₂²+…+_n²0) такие, что

приx

Было доказано, что функции линейно независимы при _i_j. Поэтому данное равенство имеет место лишь при

Так как не все _k равны нулю, то найдётся вектор , но это не соответствует определению собственных векторов матрицы. Пришли к противоречию. Следовательно, полученная система решений (7) фундаментальна, и общее решение однородной системы (1) представляется в виде

Рассмотрим ситуацию, когда среди простых корней характеристического уравнения встречаются комплексные. В этом случае представление общего решения линейной однородной системы в виде

нас не устраивает, ибо среди слагаемых есть комплекснозначные функции. Поэтому фундаментальная система решений нуждается в определённой реконструкции. Допустим, что ₁=+i. Тогда в силу действительности коэффициентов характеристического многочлена среди его корней должен присутствовать и комплексносопряжённый корень ₂=-i. Из уравнений для собственных векторов матрицы А

отвечающих собственным значениям ₁ и ₂, имеем

(8)

Применяя комплексное сопряжение к первому из уравнений (8)

и сопоставляя его с уравнением для собственного вектора , заключаем, что можно выбрать равным : = . Отсюда следует, что два линейно независимых комплекснозначных решения и линейной однородной системы также являются комплексно сопряжёнными. Из этих комплекснозначных решений можно путём линейного невырожденного преобразования получить два действительных линейно независимых решения. В самом деле, их можно построить следующим образом:

где Определитель матрицы преобразования

Таким образом, в случае простых комплексных корней линейно независимыми действительными решениями являются действительные и мнимые части комплекснозначных решений.