47. Симметричная форма системы дифференциальных уравнений. Необходимое и достаточное условие для первого интеграла симметричной системы. Интегрируемые комбинации.

Нормальную систему диф. ур-ий (1) можно переписать в другом виде:

Чтобы сделать переменные равноправными будем обозначать их через и рассмотрим систему:

(2)

Это симметричная форма системы (1). Если считать x_n независимой переменой, то придем к системе:

(3)

Таким образом, система (3) – нормальная система (n-1)-го порядка. В записи (3) полагают, что . Если в некоторой точке , то такая точка называется особой точкой. Будем полагать, что . И потребуем, чтобы все функции были непрерывно дифференцируемы по всем аргументам в некоторой области G и одновременно не обращались в нуль. При этих условиях система (3) имеет решения, непрерывно дифференцируемые по начальным условиям, и существуют первые интегралы. Если – первый интеграл системы, который непрерывно дифференцируем по всем аргументам и:

,

то справедливо необходимое и достаточное условие

Применим его для системы (3):

Умножая это уравнение на в итоге получим:

(4)

Это и есть необходимое и достаточное условие для того, чтобы функция была первым интегралом системы (2). Условие (4) можно записать в компактной форме, если ввести векторы:

Тогда (4) примет вид:

Опр. Интегрируемой комбинацией называют диф. ур-е, которое является следствием системы, но при этом легко интегрируется

Используем известный алгебраический результат. Пусть справедливы равенства:

Зададимся произвольными числами k₁,…, k_n. Тогда:

Это свойство применяется для отыскания интегрируемых комбинаций и получения первых интегралов системы(2).

57. Вид фундаментальной системы решений в случае, когда характеристическое уравнение имеет кратна корни: а) ранг характеристической матрицы г имеет наименьшее значение (r=n-m, m - кратность корня), б) m >n-m.

Пусть среди корней характеристического уравнения есть кратные. предположим, например, что корень имеет кратность m. Тогда характеристический многочлен представим в виде:

(2)

причём . Из равенства (2) следует, что

Как было показано, является суммой главных миноров (n-1)-ого порядка матрицы . Аналогично есть сумма миноров (n-2)-ого порядка той же матрицы и т.д. Выражение для представляет собой сумму главных миноров матрицы . Эта сумма отлична от нуля, поэтому хотя бы один из миноров (n-m)-ого порядка также не равен нулю. Следовательно ранг матрицы : r≥n-m. Ранг достигает минимального значения r=n-m, когда все главные миноры матрицы порядка (n-m+1) обращаются в нуль. В общем случае границы изменения ранга матрицы таковы: n-m≤r≤n-1.

Таким образом система уравнений для определения собственного вектора , отвечающего собственному значению ,

имеет r независимых уравнений, а остальные (n-r) уравнений являются их следствиями. Это означает, что (n-r) компонент собственного вектора могут быть произвольными, а остальные r компонент являются их линейными комбинациями. Положим , где c_i – произвольные постоянные, а

В результате придём к системе решений

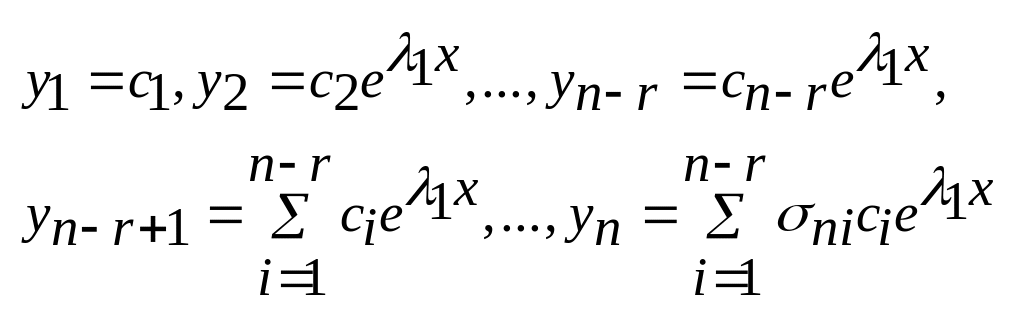
Из этих решений можно получить n-r линейно независимых. Положим , тогда

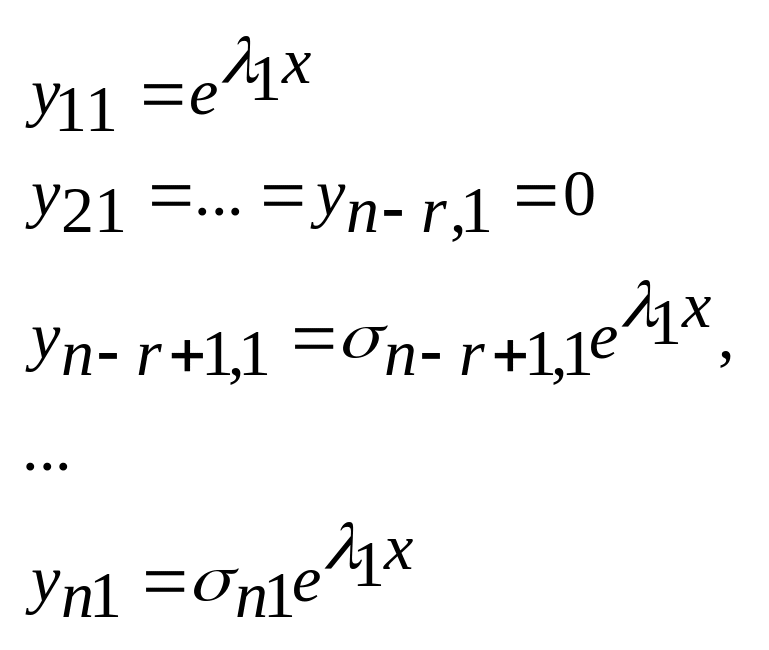
Затем находим второе решение:

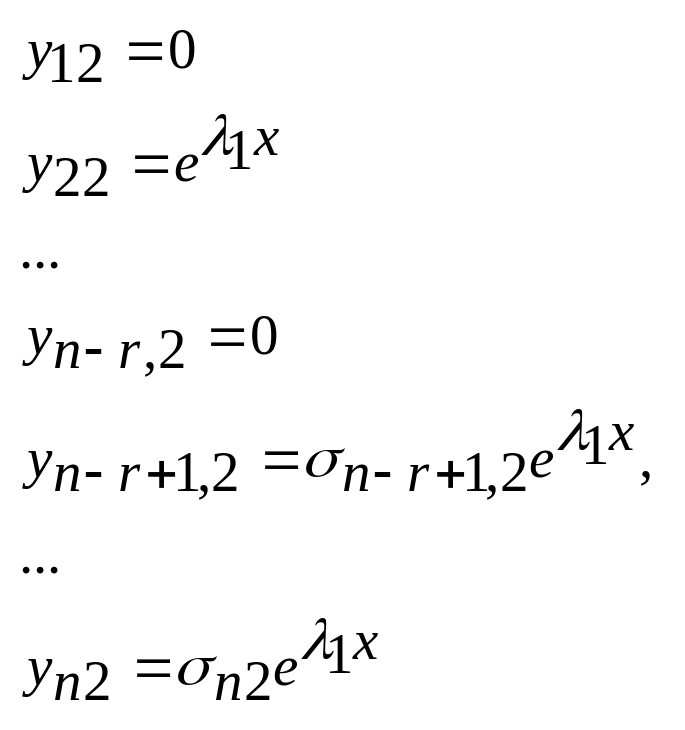
И т.д. Последнее решение получаем при подстановке

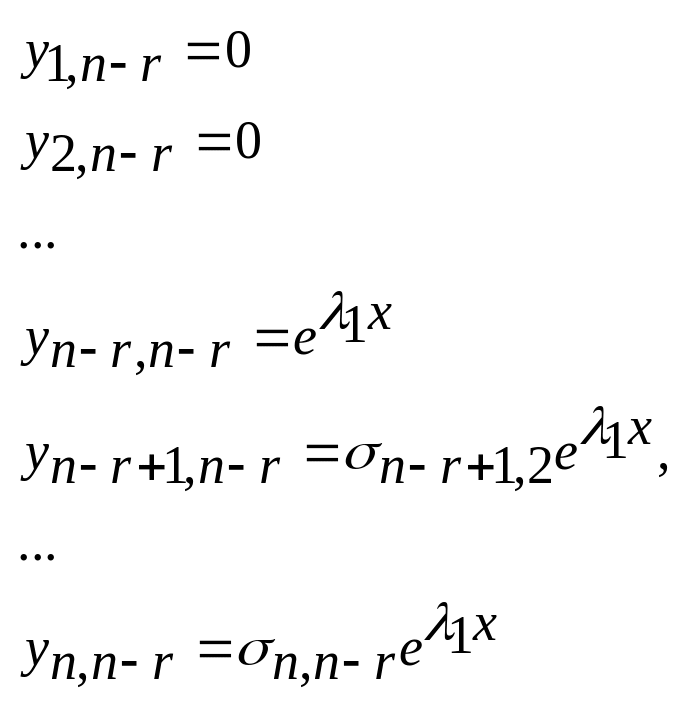
Для того, чтобы убедиться в линейной зависимости решений выпишем матрицу коэффициентов:

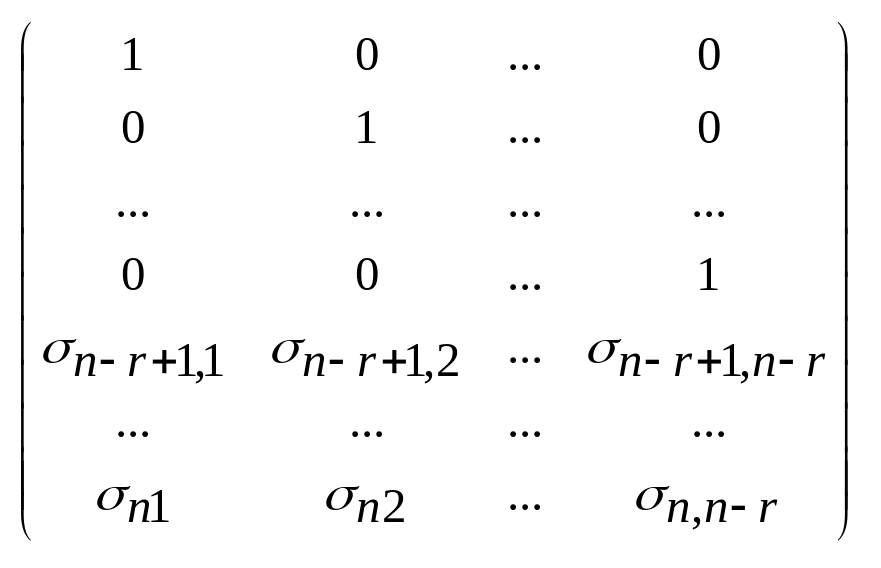
Ранг этой матрицы, имеющей размеры n x (n-r), равен (n-r), поскольку есть минор (n-r)-ого порядка, отличный от нуля. Отсюда и следует линейная независимость (n-r) построенных решений/

Если ранг матрицы имеет наименьшее значение r=n-m, то число линейно независимых решений равно n-r=m – кратность корня . А это нам и нужно для построения фундаментальной системы решений.

Если же ранг матрицы , то число построенных линейно независимых решений n-r<m. В этом случае решение системы ищут в виде :

(3)

где P_i(x) – многочлен степени m-(n-r). Заметим, что если ранг матрицы достигает своего максимального значения r=n-1, то входящий в (3) многочлен имеет степень m-1.