Удельная ёмкость

Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.

Плоский конденсатор и его емкость.

Конденсаторы состоят из двух или более близко расположенных друг к другу проводников (обкладок), разделенных слоем диэлектрика (рис. 1), причем толщина слоя диэлектрика между проводниками значительно меньше размеров самих проводников.

Рис. 1

При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников.

Обкладкам конденсатора сообщают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов, так как разноименные заряды притягиваются и поэтому располагаются на внутренних поверхностях пластин.

Под зарядом конденсатора понимают заряд одной пластины.

Электроемкостью конденсатора называют физическую величину, численно равную отношению заряда конденсатора к разности потенциалов между его обкладками:

 или 

Поле плоского конденсатора можно рассматривать как совокупность полей двух бесконечных разноименно заряженных плоскостей (рис. 2, а и б). Напряженность поля (рис. 2, в) можно найти по принципу суперпозиции:   — напряженность поля конденсатора, гдеσ — поверхностная плотность заряда на обкладках конденсатора.

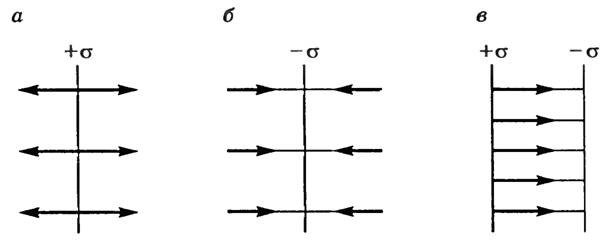
Рис. 2

Рассчитаем емкость плоского конденсатора.

Обозначим площадь одной обкладки S, расстояние между ними d. Так как  , q = σS , U = Ed, то  , где  . Следовательно, емкость плоского конденсатора

Таким образом, емкость плоского конденсатора зависит от площади обкладок, расстояния между ними и диэлектрической проницаемости диэлектрика, заполняющего пространство между обкладками конденсатора, но не зависит от материала, из которого эти пластины изготовлены.

Конденсаторы можно классифицировать по следующим признакам и свойствам:

1. по назначению — конденсаторы постоянной и переменной емкости;

2. по форме обкладок различают конденсаторы плоские, сферические, цилиндрические и др.;

3. по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и т.д.

Для получения необходимой емкости конденсаторы соединяют между собой в батареи, применяя при этом параллельное, последовательное и смешанное соединения.

Энергия заряженного конденсатора. Обьемная плотность энергии электростатического поля.

Энергия заряженного конденсатора

Если на обкладках конденсатора электроемкостью С находятся электрические заряды +q и -q, то согласно формуле (20.1) напряжение между обкладками конденсатора равно

В процессе разрядки конденсатора напряжение между его обкладками убывает прямо пропорционально заряду q от первоначального значения U до 0.

Среднее значение напряжения в процессе разрядки равно

Для работы А, совершаемой электрическим полем при разрядке конденсатора, будем иметь:

Следовательно, потенциальная энергия W_p конденсатора электроемкостью С, заряженного до напряжения U, равна

Энергия конденсатора обусловлена тем, что электрическое поле между его обкладками обладает энергией. Напряженность Е поля пропорциональна напряжению U, поэтому энергия электрического поля пропорциональна квадрату его напряженности.

Обьемная плотность энергии электростатического поля.

Это физическая величина, численно равная отношению потенциальной энергии поля, заключенной в элементе объема, к этому объему. Для однородного поля объемная плотность энергии равна   . Для плоского конденсатора, объем которого Sd, где S - площадь пластин, d - расстояние между пластинами, имеем

С учетом, что   и 

(16.4)

или