
- •1 Постановка злп.
- •2 Запишите злп в форме озлп.
- •3 Запишите злп в форме ОснЗлп.
- •4 Запишите злп в форме кзлп
- •5 Приведите озлп к каноническому виду.
- •7 Перечислите свойства множества планов р
- •8 Дайте определение оптимального плана кзлп.
- •15 Что называется линией уровня целевой функции?
- •31 Где в алгоритме симплекс-метода используется метод Гаусса?
- •32 Дайте определение р-матрицы кзлп.
- •33 Дайте определение псевдоплана кзлп.
- •34 Сформулируйте критерий отсутствия решения в алгоритме р-метода
- •35 В каком случае к решению злп необходимо применять двухэтапный симплекс-метод?
- •36 Какие злп не могут быть решены симплекс-методом?
31 Где в алгоритме симплекс-метода используется метод Гаусса?
ПЕРЕХОД ОТ ОДНОЙ К-МАТРИЦЫ ЗЛП К ДРУГОЙ К-МАТРИЦЕ
Пусть известна К-матрица
 .
.
Обозначим
через
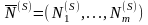 вектор номеров базисных (единичных)
столбцов матрицы
,
вектор номеров базисных (единичных)
столбцов матрицы
,
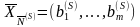 – вектор, компоненты которого есть
базисные компоненты опорного плана,
определяемого матрицей
,
и могут быть отличны от нуля. Остальные
(n-m)
компонент опорного плана, определяемого
матрицей
,
равны нулю. Очевидно, что векторы
и
полностью
задают опорный план, определяемый
матрицей
.
Например, пусть
– вектор, компоненты которого есть
базисные компоненты опорного плана,
определяемого матрицей
,
и могут быть отличны от нуля. Остальные
(n-m)
компонент опорного плана, определяемого
матрицей
,
равны нулю. Очевидно, что векторы
и
полностью
задают опорный план, определяемый
матрицей
.
Например, пусть
=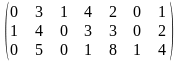 ,
,
тогда
=
(3, 1, 6);
=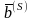 =
(1, 2, 4) и, следовательно, опорный план,
определяемый
,
имеет вид
=
(1, 2, 4) и, следовательно, опорный план,
определяемый
,
имеет вид
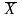 =
(2, 0, 1, 0, 0, 4).
=
(2, 0, 1, 0, 0, 4).
Итак, пусть К-матрица (3.45) определяет невырожденный опорный план
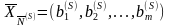
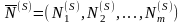 .
(3.46)
.
(3.46)
Выберем в матрице столбец , не принадлежащий единичной подматрице, т.е. , , и такой, что в этом столбце есть хотя бы один элемент больше нуля.
Пусть
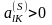 .
Считая
.
Считая
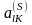 направляющим
элементом, совершим над матрицей
один шаг метода Жордана–Гаусса. В
результате получим новую матрицу
направляющим
элементом, совершим над матрицей
один шаг метода Жордана–Гаусса. В
результате получим новую матрицу
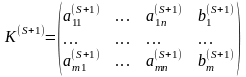 в
которой столбец
стал единичным, но которая может и не
быть К-матрицей, так как среди величин
в
которой столбец
стал единичным, но которая может и не
быть К-матрицей, так как среди величин
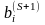 могут
быть отрицательные. Условия выбора
направляющего элемента
могут
быть отрицательные. Условия выбора
направляющего элемента
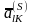 ,
позволяющие получить новую К-матрицу
,
позволяющие получить новую К-матрицу
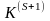 ,
т.е. обосновывающие способ перехода от
опорного плана
,
т.е. обосновывающие способ перехода от
опорного плана
![]() к
опорному плану
к
опорному плану
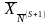 ,
составляют содержание следующей теоремы,
которая была доказана выше:
,
составляют содержание следующей теоремы,
которая была доказана выше:
32 Дайте определение р-матрицы кзлп.
Р-матрица КЗЛП – расширенная матрица системы линейных уравнений, равносильной исходной системе, содержащая единичную подматрицу порядка m на месте n первых столбцов, все симплекс-разности которой неотрицательны. Очевидно, что всякая Р-матрица ЗЛП определяет некоторое базисное решение системы уравнений
33 Дайте определение псевдоплана кзлп.
Базисное решение системы линейных уравнений, определяемое Р-матрицей, называется псевдопланом ЗЛП.
34 Сформулируйте критерий отсутствия решения в алгоритме р-метода
Алгоритмдвойственногосимплекс-метода:
1)выбирают разрешающую строку по наибольшему по абсолютной величине отрицательному элементу столбца свободных членов;
2)выбирают разрешающий столбец по наименьшему по абсолютной величине отношению элементов L строки к отрицательным элементам разрешающей строки;
3) пересчитываютсимплекснуютаблицупоправиламобычногосимплекс-метода;
4) решение проверяют на оптимальность. Признаком получения допустимого оптимального решения является отсутствие в столбце свободных членов отрицательных элементов.
35 В каком случае к решению злп необходимо применять двухэтапный симплекс-метод?
Рассмотрим задачу
![]() =
0,4X1+ 0,3X2 + 0,1X3 + 0,1X5 +
0,2X6 (3.71)
=
0,4X1+ 0,3X2 + 0,1X3 + 0,1X5 +
0,2X6 (3.71)
2X2 + 2X3 + 4X4 + X5 = 150
X1 + X2 + 2X5 = 200 (3.72)
X1 + X3 + 2X6 = 300
![]() ;
j = 1,...,6 (3.73)
;
j = 1,...,6 (3.73)
Так
как ограничения (3.72) рассматриваемой
ЗЛП уже имеют вид строгих равенств, то
для приведения ее к каноническому виду
достаточно только изменить знак функции
на
противоположный и рассмотреть задачу
нахождения
![]() –0,4X1
– 0,3X2
–
–
0,1X3 – 0,1X5 – 0,2X6 (3.74) при
тех же ограничениях (3.72)–(3.73).
–0,4X1
– 0,3X2
–
–
0,1X3 – 0,1X5 – 0,2X6 (3.74) при
тех же ограничениях (3.72)–(3.73).
Рассмотрим расширенную матрицу А системы уравнений (3.72)

Так как матрица А не содержит единичной подматрицы порядка 3, то она не является К-матрицей ЗЛП и, следовательно, к задаче (3.71)–(3.73) не может быть применен симплекс-метод.
Рассмотрим метод отыскания исходного опорного плана (К-матрицы)- метод искусcтвенного базиса.
ПЕРВЫЙ ЭТАП – РЕШЕНИЕ ВСПОМОГАТЕЛЬНОЙ ЗАДАЧИ
ВТОРОЙ ЭТАП – РЕШЕНИЕ ИСХОДНОЙ ЗАДАЧИ
