15 Что называется линией уровня целевой функции?

Линией уровня функции называется множество точек из ее области определения, в которых функция принимает одно и то же фиксированное значение. Градиентом функции f(x) называется вектор указывающий направление наиболее быстрого возрастания функции, и, стало быть, ориентированный перпендикулярно линиям уровня. Для линейной функции двух переменных линия уровня представляет собой прямую, перпендикулярную вектору с, который служит градиентом данной функции. Следовательно, если линия уровня определяется уравнением f(x)=c1x1+ c2x2 =const, то этот вектор имеет вид 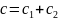и указывает направление возрастания функции.

С₁Х₁ + С₂Х₂ = const – линия уровня функции 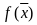, перпендикулярную вектору-градиенту

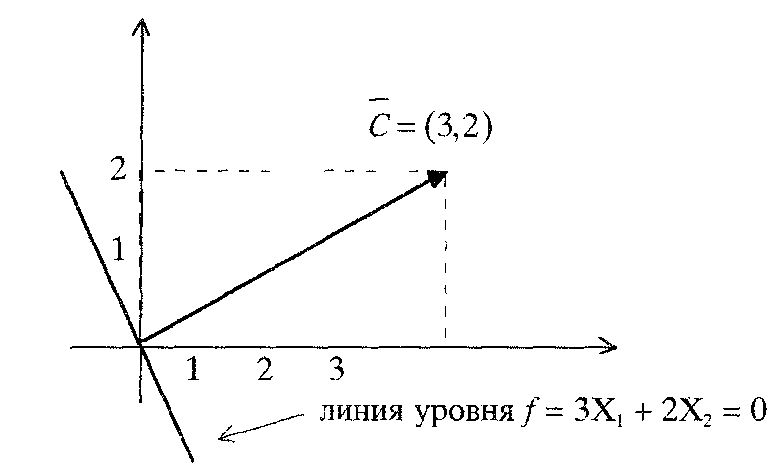
16 В каких случаях при решении ЗЛП графическим методом можно убедиться в ее неразрешимости? Задача линейного программирования называется разрешимой, если она имеет хотя бы одно оптимальное решение. У неразрешимой задачи или пуста область допустимых решений, или целевая функция не ограничена.

Если допустимая область решений Р представляет собой неограниченную область и прямая при движении в направлении вектора (или противоположном ему) не покидает Р, то в этом случае не ограничена сверху (или снизу), т.е. (или ).

17 Что означает разрешимость ЗЛП при графическом методе ее решения?

Ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи. Будем говорить, что задача линейного программирования разрешима, если она имеет хотя бы один оптимальный план.

ЗЛП разрешима, то есть существует такая точка , что .

18 Запишите КЗЛП в алгебраической форме.

КЗЛП имеет вид:

(3.10)

, (3.11)

(3.12)

19 Запишите КЗЛП в векторно-матричной форме.

(3.13)

(3.14)

(3.15)

20 Дайте определение опорного плана КЗЛП.

_{Опорным планом (ОП) задачи линейного программирования будем называть такой ее план, который является базисным решением системы линейных уравнений .}

_{(План или допустимое решение задачи линейного программирования – вектор пространства Еn, компоненты которого удовлетворяют функциональным и прямым ограничениям задачи.)}

_{Согласно определению и предположению о том, что r(A) = m} , всякому опорному плану задачи линейного программирования (как и всякому базисному решению системы линейных уравнений ) соответствует базисная подматрица В порядка m матрицы А и определенный набор m базисных переменных системы линейных уравнений .

Определение. m компонент базисного решения системы линейных уравнений , являющихся значениями соответствующих ему базисных переменных, будем называть базисными компонентами этого решения.

Отметим, что базисные компоненты опорного плана неотрицательны; остальные n-m его компонент равны нулю. Очевидно, что число опорных планов задачи линейного программирования конечно и не превышает . Число строго положительных компонент опорного плана не превышает m.

21Дайте определение К-матрицы КЗЛП.

К-матрицей КЗЛП будем называть расширенную матрицу системы линейных уравнений, равносильной системе 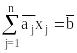, содержащую единичную подматрицу на месте первых n своих столбцов и все элементы ( n+1 )-го столбца которой неотрицательны.

Число К-матриц конечно и не превышает . Каждая К-матрица определяет ОП КЗЛП и наоборот.

22 Сформулируйте связь между опорным планом и К-матрицей.

Каждая К-матрица определяет ОП КЗЛП и наоборот.

23 Число опорных планов конечно или нет?

Число опорных планов задачи линейного программирования конечно и не превышает . Число строго положительных компонент опорного плана не превышает m.

24 Какого числа не превышает количество опорных планов КЗЛП?

Число опорных планов задачи линейного программирования конечно и не превышает . Число строго положительных компонент опорного плана не превышает m.

m -ранг матрицы А системы уравнений , причем m < n.

m компонент базисного решения системы линейных уравнений , являющихся значениями соответствующих ему базисных переменных, будем называть базисными компонентами этого решения.

Отметим, что базисные компоненты опорного плана неотрицательны; остальные n-m его компонент равны нулю.

25 Сформулируйте связь между опорным планом и крайней точкой.

Теорема (о крайней точке). Опорный план ЗЛП является крайней точкой множества P’ и наоборот.

Следствие 1. Крайняя точка множества P’ может иметь не более m строго положительных компонент.

Следствие 2. Число крайних точек множества P’ конечно и не превышает .

Следствие 3. Если множество P’ ограниченное, то оно является выпуклым многогранником.

26 Сформулируйте утверждение о существовании оптимального опорного плана.

Теорема 3.3 (о существовании опорного плана или решения ЗЛП). Если линейная форма ограничена сверху на непустом множестве P’, то ЗЛП разрешима, то есть существует такая точка , что .

Теорема 3.4. Если множество P’ не пусто, то оно имеет опорный план (или крайнюю точку).

27 Дайте определение симплекс-разности.

Величину

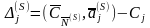, (3.49)

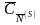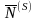где – вектор, компонентами которого являются коэффициенты линейной функции при базисных ( ) переменных опорного плана, определяемого матрицей 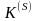, назовем j-й симплекс-разностью матрицы .

28 Сформулируйте критерий оптимальности в алгоритме симплекс-метода.

_{Теорема (критерий оптимальности опорного плана). Пусть все симплекс-разности матрицы} неотрицательные. Тогда опорный план 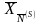, определяемый матрицей , является оптимальным.

29 Сформулируйте критерий отсутствия решений в алгоритме симплекс-метода.

Пусть в матрице есть симлекс-разности 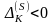и в столбце 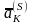( 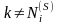, 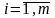) нет ни одного строго положительного элемента. Тогда ЗЛП (3.18) не имеет конечного решения.

30 Сформулируйте основные моменты, которые должен содержать любой конечный алгоритм решения ЗЛП.

Решением задачи является неотрицательное базисное решение системы линейных уравнений , то метод решения задачи должен содержать четыре момента:

1. обоснование способа перехода от одного опорного плана (К-матрицы) к другому;

2. указание признака оптимальности, позволяющего проверить, является ли данный опорный план оптимальным;

3. указание способа построения нового опорного плана, более близкого к оптимальному;

4. указание признака отсутствия конечного решения.