18.Однородная система линейных уравнений и её фундаментальная система решений.

Однородные системы линейных уравнений

Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.

Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

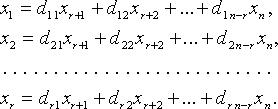
Тогда n - r линейно независимыми вектор-решениями будут:

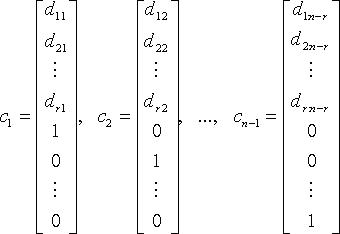
а любое другое решение является их линейной комбинацией. Вектор-решения образуют нормированную фундаментальную систему.

В линейном пространстве множество решений однородной системы линейных уравнений образует подпространство размерности n - r; - базис этого подпространства.

19. Собственные значения и собственные векторы матрицы. Характеристическое уравнение матрицы.

Собственные векторы и собственные значения

Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A, если

Av = λv,

где число λ называется собственным значением матрицы A. Таким образом преобразование, которое выполняет матрица A над вектором v, сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v — собственный вектор, то и αv — тоже собственный вектор.

2.7. Собственные значения

У матрицы A , размерностью (N×N) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению

det(A − λI) = 0,

являющемуся алгебраическим уравнением N-го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид

Например,

Рис. 21 Собственные значения

Набор собственных значений λ₁,..., λ_N матрицы A называется спектром A.

Спектр обладает разнообразными свойствами. В частности

det(A) = λ₁×...×λ_N, Sp(A) = λ₁+...+λ_N.

Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная (A^t = A), то ее собственные значения вещественны.

2.8. Собственные векторы

У матрицы A, размерностью (N×N) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора v_n нужно решить систему однородных уравнений

(A − λ_nI) v_n = 0.

Она имеет нетривиальное решение, поскольку det(A − λ_nI) = 0.

Например,

Рис. 22 Собственные вектора

Собственные вектора симметричной матрицы ортогональны.

23.

Нормальное уравнение прямой. Расстояние от данной точки до данной прямой

1. Нормальное уравнение прямой

где p - длина перпендикуляра (нормали), опущенного из начала координат на прямую, а - угол наклона этого перпендикуляра к оси Ox. Чтобы привести общее уравнение прямой Ax + By + C = 0 к нормальному виду, нужно все члены его умножить на нормирующий множитель , взятый со знаком, противоположным знаку свободного члена C.

2. Расстояние точки A(x₁, y₁) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле

Правило. Чтобы определить расстояние точки A(x₁, y₁) до прямой Ax + By + C = 0, нужно привести уравнение прямой к нормальному виду, взять левую часть полученного уравнения и подставить в нее вместо текущих координат координаты данной точки. Абсолютная величина полученного числа и даст искомое расстояние:

Расстояние от точки до прямой есть всегда величина положительная. Кроме расстояния от точки до прямой, рассматривается еще так называемое отклонение точки от прямой.

Отклонение данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.

Расстояние от точки до прямой есть абсолютная величина отклонения этой точки от прямой.