13.Обратная матрица. Метод нахождения обратной матрицы по методу Гаусса.

По данному методу к данной матрице приписывают единичную того же порядка что и исходная , затем при помощи элементарных преобразований исходная матрица приводится к единичной, а на месте единичной матрицы получается обрстная.

14. Системы линейных алгебраических уравнений. Теорема Кронекера-Капелли. Бесконечное множество решений. . Основные понятия Общий вид и свойства системы уравнений

Система т линейных уравнений с п неизвестными (пере­менными) x₁, x₂, ..., x_п имеет вид

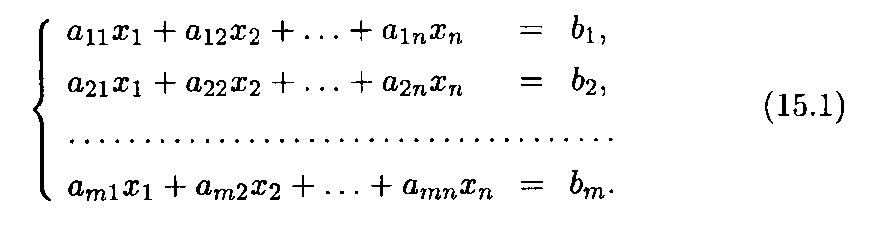
Здесь a_ij и b_i — произвольные числа (i = 1, 2,..., m; j = 1, 2, ..., n), которые называются соответственно коэффици­ентами при неизвестных и свободными членами уравнений (15.1). Первый индекс у коэффициентов при неизвестных озна­чает номер уравнения, второй индекс соответствует номеру не­известного x_i.

Решением системы уравнений (15.1) называется набор п чисел x₁ = α₁, x₂ = α₂, … , x_n = α_n, при подстановке которых в эту систему каждое уравнение данной системы превращается в тождество.

Система уравнений (15.1) называется совместной, если она имеет хотя бы одно решение; если система не имеет решений, она называется несовместной. Совместная система уравнений имеет либо одно решение, и в таком случае она называется определенной, либо, если у нее больше одного решения, она называется неопределенной.

Системы уравнений вида (15.1) называются эквивалент­ными, если они имеют одно и то же множество решений. Эле­ментарные преобразования исходной системы приводят к эк­вивалентной системе. К элементарным преобразованиям отно­сятся:

• вычеркивание уравнения 0x₁ + 0x₂ + ... + 0х_n = 0 — нулевой строки;

• перестановка уравнений или слагаемых a_ijx_j в уравне­ниях;

• прибавление к обеим частям одного уравнения соответ­ственно обеих частей другого уравнения этой системы, умноженного на любое действительное число;

• удаление уравнений, являющихся линейными комбина­циями других уравнений системы.

Последнее свойство вытекает из третьего свойства: если какое-либо уравнение представляет собой линейную комбина­цию других уравнений, то из него можно сформировать нуле­вую строку.

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Доказательство (условия совместности системы)

Необходимость

Пусть система совместна. Тогда существуют числа такие, что . Следовательно, столбец является линейной комбинацией столбцов матрицы . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .

Достаточность

Пусть . Возьмем в матрице какой-нибудь базисный минор. Так как , то он же и будет базисным минором и матрицы . Тогда согласно теореме о базисном миноре последний столбец матрицы будет линейной комбинацией базисных столбцов, то есть столбцов матрицы . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы .