- •1.Множества. Операции над множествами. Применение операций над множествами при решении задач.
- •2.Свойства операций над множествами. Примеры.
- •3. Числовые множества и их свойства. Числовая прямая и множества на ней.
- •4.Арифметические векторы. Линейные операции над векторами. Скалярное произведение векторов и его свойства. Ы-мерное векторное пространство.
- •5.Угол между векторами. Условие перпендикулярности векторов. Условие коллинеарности векторов.
- •Линейные операции над матрицами
- •7.Транспонирование матриц
- •Умножение матриц
- •8. Ранг матрицы
- •9. Определители второго и третьего порядков. Способы их вычисления.
- •10. Миноры и алгебраические дополнения. Определитель п-го порядка. Разложение определителя по элементам ряда.
- •Миноры и алгебраические дополнения
- •11. Свойства определителей. Вычисление определителя с использованием его свойств.
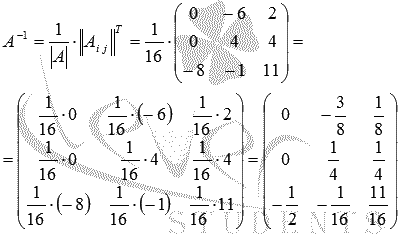
- •12. Обратная матрица. Метод нахождения обратной матрицы по формуле.
- •13.Обратная матрица. Метод нахождения обратной матрицы по методу Гаусса.
- •14. Системы линейных алгебраических уравнений. Теорема Кронекера-Капелли. Бесконечное множество решений. . Основные понятия Общий вид и свойства системы уравнений
- •15.Решение систем линейных алгебраических уравнений по формулам Крамера.
- •16.Решение систем линейных алгебраических уравнений методом обратной матрицы
- •17. Матрица системы линейных уравнений. Расширенная матрица системы. Решение системы линейных уравнений методом Гаусса. Матричная форма системы уравнений
- •18.Однородная система линейных уравнений и её фундаментальная система решений.
- •19. Собственные значения и собственные векторы матрицы. Характеристическое уравнение матрицы.
- •2.7. Собственные значения
- •2.8. Собственные векторы
11. Свойства определителей. Вычисление определителя с использованием его свойств.
Основные свойства определителей
Из данного выше общего определения следуют основные свойства определителей.
1. Если некоторая строка или столбец определителя состоит из нулей, то определитель равен нулю.
Действительно, согласно общему определению, в каждое из n! слагаемых обязательно войдет сомножителем элемент нулевой строки (нулевого столбца).
2. При перестановке двух строк (столбцов) определитель меняет знак.
Это свойство легко проверяется на определителях второго и третьего порядков.
3. Определитель, содержащий две одинаковые строки (два одинаковых столбца), равен нулю.
Действительно, поменяв местами эти строки, получаем Δn = -Δn откуда и следует, что Δn = 0.
4. Общий множитель любой строки (столбца) можно вынести за знак определителя.
5. Если каждый элемент некоторой строки (столбца) определителя Δn представлен в виде суммы двух слагаемых, то этот определитель равен сумме двух определителей, в каждом из которых: а) все строки (столбцы), за исключением указанной строки (столбца), совпадают с аналогичными строками (столбцами) определителя Δn; б) на месте указанной строки (столбца) первый определитель содержит первые слагаемые, а второй определитель — вторые слагаемые данной строки (столбца) определителя Δn.
Поясним это свойство на примере определителя третьего порядка:
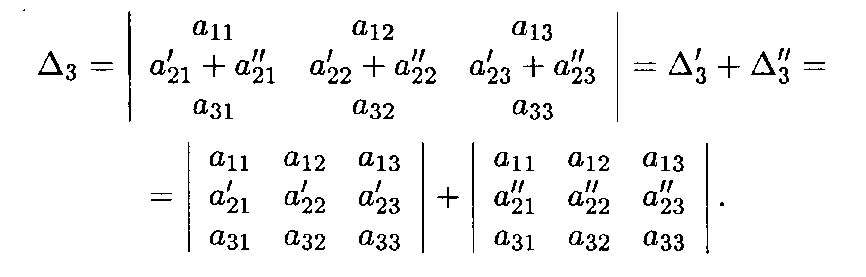
6. Определитель не изменится, если к элементам любой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на любое число.
Это свойство является следствием свойств 3-5.
7. При транспонировании матрицы определитель не меняется.
Из перечисленных свойств следует, что определитель равен нулю, если по крайней мере одна из его строк (столбцов) является линейной комбинацией каких-либо других его строк (столбцов). Отсюда вытекает необходимое и достаточное условие равенства нулю определителя. Определитель равен нулю тогда и только тогда, когда его строки (столбцы) линейно зависимы.
12. Обратная матрица. Метод нахождения обратной матрицы по формуле.
Составим
алгоритм
нахождения обратной матрицы
с использованием равенства
 .
.
Вычисляем определитель матрицы А и убеждаемся, что он отличен от нуля (в противном случае матрица А необратима).
Строим
 -
матрицу из алгебраических дополнений
элементов
-
матрицу из алгебраических дополнений
элементов
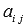 .
.
Транспонируем матрицу , тем самым получаем
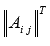 .
.
Умножаем каждый элемент матрицы на число
 .
Этой операцией завершается нахождение
обратной матрицы
.
Этой операцией завершается нахождение
обратной матрицы
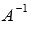 .
.
Проводим проверку результата, вычисляя произведения
 и
и
 .
Если
.
Если
 ,
то обратная матрица найдена верно, в
противном случае где-то была допущена
ошибка.
,
то обратная матрица найдена верно, в
противном случае где-то была допущена
ошибка.
Разберем
алгоритм нахождения обратной матрицы
на примере.
Пример.
Дана
матрица
 .
Найдите обратную матрицу.
Решение.
Вычислим
определитель матрицы А,
разложив его по элементам третьего
столбца:
.
Найдите обратную матрицу.
Решение.
Вычислим
определитель матрицы А,
разложив его по элементам третьего
столбца:
 Определитель
отличен от нуля, так что матрица А
обратима.
Найдем матрицу из
алгебраических дополнений:
Определитель
отличен от нуля, так что матрица А
обратима.
Найдем матрицу из
алгебраических дополнений:

Поэтому
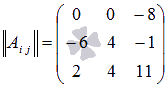 Выполним
транспонирование матрицы из алгебраических
дополнений:
Выполним
транспонирование матрицы из алгебраических
дополнений:
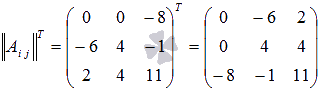 Теперь
находим обратную матрицу как
:
Теперь
находим обратную матрицу как
: