15.Решение систем линейных алгебраических уравнений по формулам Крамера.

ТЕОРЕМА 2 (правило Крамера). Пусть Δ — определитель матрицы системы А, а Δ_j — определитель, полученный из определителя Δ заменой j-го столбца столбцом свободных членов В. Тогда если Δ ≠ 0, то система линейных уравнений (15.5) имеет единственное решение, определяемое по форму­лам

Формулы вычисления неизвестных (15.6) — решения сис­темы (15.5) — носят название формул Крамера.

Пример 1. Найти решение системы уравнений

Решение. Составим и вычислим определители системы Δ и Δ_j (j = x, y, z):

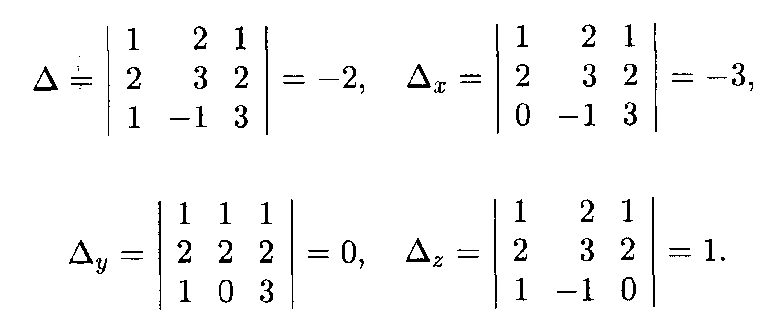
Определитель системы отличен от нуля, стало быть, она имеет единственное решение, которое вычисляется по форму­лам (15.6):

16.Решение систем линейных алгебраических уравнений методом обратной матрицы

Пусть система линейных алгебраических уравнений задана в матричной форме , где матрица A имеет размерность n на n и ее определитель отличен от нуля. Так как , то матрица А – обратима, то есть, существует обратная матрица . Если умножить обе части равенства на слева, то получим формулу для нахождения матрицы-столбца неизвестных переменных . Так мы получили решение системы линейных алгебраических уравнений матричным методом. Пример. 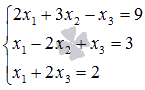Решите систему линейных уравнений матричным методом. Решение. Перепишем систему уравнений в матричной форме: Так как то СЛАУ можно решать матричным методом. С помощью обратной матрицы решение этой системы может быть найдено как . 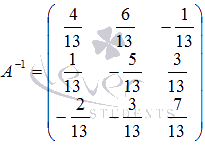Построим обратную матрицу с помощью матрицы из алгебраических дополнений элементов матрицы А (при необходимости смотрите статью методы нахождения обратной матрицы): Осталось вычислить 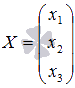- матрицу неизвестных переменных, умножив обратную матрицу на матрицу-столбец свободных членов 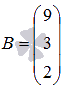(при необходимости смотрите статью операции над матрицами): 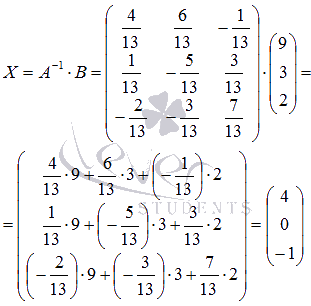Ответ: 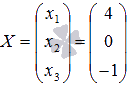или в другой записи x₁ = 4, x₂ = 0, x₃ = -1. Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего. Более подробное описание теории и дополнительные примеры смотрите в статье матричный метод решения систем линейных уравнений.

17. Матрица системы линейных уравнений. Расширенная матрица системы. Решение системы линейных уравнений методом Гаусса. Матричная форма системы уравнений

Сведем коэффициенты при неизвестных в системе уравне­ний (15.1) в матрицу

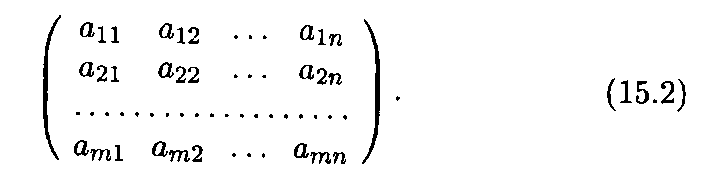
Эта матрица состоит из m строк и п столбцов и называет­ся матрицей системы. Введем в рассмотрение две матрицы-столбца: матрицу неизвестных Х и матрицу свободных чле­нов В:

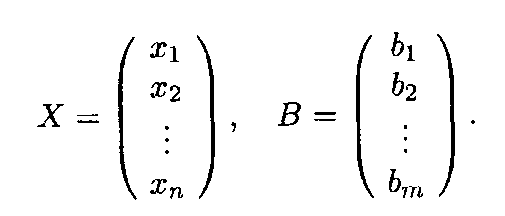
Х и В представляют собой векторы-столбцы, однако в целях единого подхода в рамках матричной алгебры удобнее тракто­вать их именно как матрицы, состоящие соответственно из п и m строк и одного столбца.

Тогда систему линейных уравнений (15.1) можно записать в матричной форме, поскольку размер матрицы А равен т х n, а размер Х — n х 1 и, значит, произведение этих матриц имеет смысл:

Произведение матриц АХ является, как и В, матрицей-столб­цом размером т х 1, состоящей из левых частей уравнений сис­темы (15.1). Все уравнения этой системы вытекают из уравне­ния (15.3) в силу определения равенства двух матриц (п. 13.1).

Введем в рассмотрение еще одну матрицу; дополним мат­рицу системы А столбцом свободных членов и получим новую матрицу размером т х (n + 1):

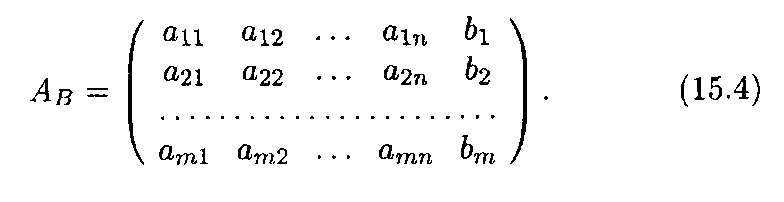
Матрица А_В называется расширенной матрицей системы. Эта матрица играет важную роль в вопросе о разрешимости системы уравнений.

Матрица может состоять как из одной строчки, так и из одного столбца. Возможно, что матрица – это одно число, или число столбцов не равно числу строк. В данном примере все уравнения приравниваются к нулю. Такая система называется однородной. Однако как мы знаем, далеко не обязательно, чтобы уравнения приравнивались к нулю. Если В – это матрица-столбец, составленная из свободных членов СЛАУ, то матрица (А|В) называется расширенной матрицей СЛАУ:

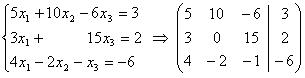
Расширенная матрица системы

Мы научились составлять матрицу СЛАУ. Теперь рассмотрим действия, которые мы можем применять к матрице. Над строками матрицы можно проводить элементарные преобразования: 1) Переставлять местами 2 уравнения СЛАУ (2 строчки матрицы СЛАУ); 2) Умножать какое-либо уравнение СЛАУ (строчку матрицы) на число α≠0; 3) Прибавлять к одному уравнению СЛАУ (строчке матрицы) другое её уравнение (другую её строчку), умноженное на любое число β.

Метод Гаусса

Следует заметить, что как метод обратной матрицы, так и метод Крамера являются очень трудоемкими по количест­ву вычислительной работы. Оба они требуют порядка n²n! арифметических действий для нахождения решения системы линейных уравнений. При п = 5 это составит около 3000 дей­ствий, при п = 10 — около 3,6 ∙ 10⁸ действий. При решении серьезных задач приходится иметь дело с системами уравне­ний порядка п = 100 и более. При таких масштабах даже су­перкомпьютерам потребуется огромное время для вычисления решения. Кроме того, погрешности компьютерного округления чисел приводят к значительным ошибкам в расчетах численно­го решения систем уравнений большого порядка. Между тем существуют более экономичные методы решения систем ли­нейных уравнений, основанные на предварительном преобра­зовании расширенной матрицы системы к специальному виду. В частности, одним из них является метод Гаусса, практичес­кую реализацию которого мы приводим ниже.

Рассмотрим систему уравнений общего вида (15.1). Пусть для определенности a₁₁ ≠ 0 (если a₁₁ = 0, то можно переста­вить на первое место ненулевое слагаемое или начать с другого уравнения). Умножим первое уравнение системы (15.1) на чис­ло a₂₁/a₁₁ и затем вычтем его из второго уравнения этой системы. Умножим обе части первого уравнения на число a₃₁/a₁₁ и затем вычтем его из третьего уравнения и так далее, т.е. процесс заключается в последовательном вычитании первого уравнения, умножаемого на числа a_i1/a₁₁, из i-го уравнения (i = 2, 3, ... , m). Таким образом, в результате элементарных преобразований мы получим эквивалентную систему, в кото­рой начиная со второго уравнения отсутствуют слагаемые, со­держащие неизвестное x₁:

где верхний индекс в скобках означает новые коэффициенты, полученные после первого шага. Для удобства записи будем оперировать расширенной матрицей системы, отделяя в ней вертикальной чертой столбец свободных членов. Итак, после первого шага, содержащего (т — 1) элементарных преобразо­ваний системы, мы переходим от расширенной матрицы (15.4) исходной системы к расширенной матрице

Второй шаг заключается в том, что теперь второе уравне­ние системы (15.7) или вторая строка матрицы (15.8) исполь­зуется для аналогичных элементарных преобразований строк с третьей по m-ю: эта строка последовательно умножается на число и вычитается из i-й строки (i = 3, 4, ... ,m). В результате этих (m - 2) элементарных преобразований полу­чаем новую расширенную матрицу, соответствующую новой эквивалентной системе уравнений. Эта матрица имеет вид

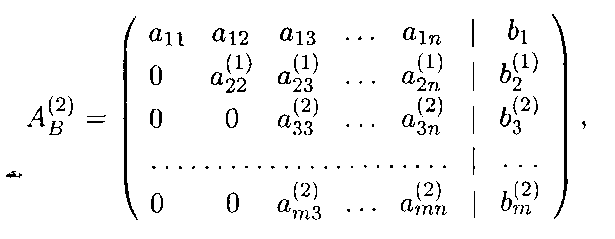
где верхний индекс означает новые коэффициенты. В случае если элемент = 0, то второе уравнение можно поменять местами с другим уравнением, у которого элемент ≠ 0.

Продолжим этот процесс аналогичным образом (т.е. на 3-м шаге преобразуются строки с 4-й по т-ю, на 4-м шаге — стро­ки с 5-й по m-ю и т.д.) до тех пор, пока не дойдем до последней m-й строки. После (r - 1)-го шага процесса последовательного исключения неизвестных мы получим следующую расширен­ную матрицу:

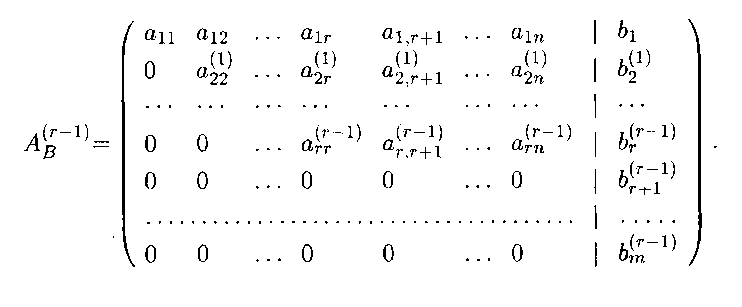
Последние (m - r) строк этой матрицы соответствуют урав­нениям эквивалентной системы уравнений

Эти уравнения могут появиться, если соответствующие урав­нения исходной системы (15.1) представляют собой линейные комбинации других уравнений этой системы, о чем говорилось в п. 15.1. Здесь мы не исследовали заранее систему (15.1) на совместность; поэтому если эта система несовместна, то хотя бы одно из чисел , ,..., не равно нулю. Таким образом, метод Гаусса позволяет на определенном шаге устано­вить возможную несовместность исходной системы линейных уравнений или выявить и удалить уравнения, являющиеся ли­нейными комбинациями других уравнений системы (15.1), если она совместна.

Пусть система (15.1) совместна, тогда все правые части уравнений (15.10) равны нулю, и после удаления нулевых урав­нений в эквивалентной системе и нулевых строк в расширенной матрице получаем матрицу специфического ступенчатого ви­да, ранг которой равен r. Все элементы этой матрицы, стоящие слева или ниже элементов а_ij, равны нулю:

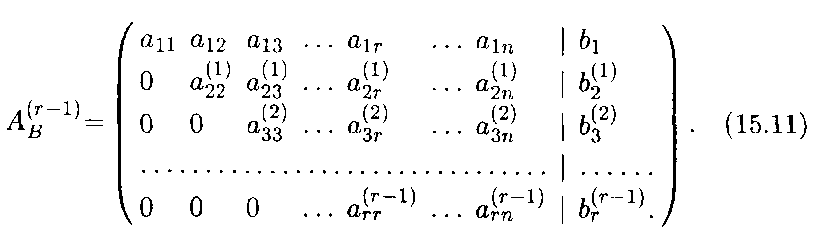
Эта расширенная матрица соответствует системе уравнений ранга r, которая имеет вид

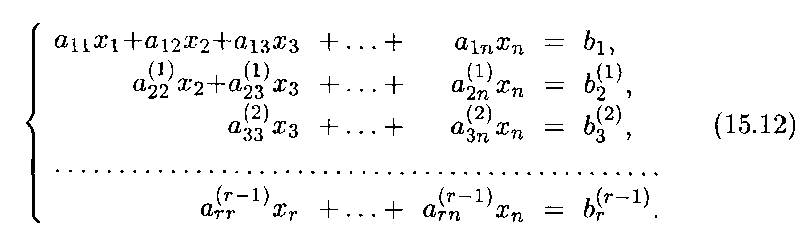
Система уравнений (15.12) уже полностью подготовлена к на­хождению решения, процесс которого осуществляется снизу вверх, т.е. от последнего уравнения к первому. Переход от сис­темы (15.1) к эквивалентной ей системе (15.12) называется пря­мым ходом, а нахождение неизвестных из системы (15.12) — обратным ходом метода Гаусса. Далее последовательность действий аналогична изложенной выше.

1. Если r = n, то система (15.12) имеет вид

Поднимаясь снизу вверх, последовательно находим (обратный ход метода Гаусса):

— из последнего r-го уравнения неизвестное x_r = ;

— из (r - 1)-го уравнения неизвестное x_r-1 путем подста­новки в это уравнение уже найденного неизвестного x_r;

— из i-го уравнения неизвестное x_i при подстановке в него найденных величин x_r, x_r-1, ..., x_i-1;

— и так далее до первого уравнения, из которого при под­становке в него уже найденных величин x_r, x_r-1 , ..., x₂ находим х₁.

2. Ранг системы уравнений (15.12) меньше n. В этом слу­чае, как и ранее, объявляем неизвестные x_r+1, x_r+2, …, x_п, сво­бодными и формируем правые части уравнений (15.12), остав­ляя в левых частях слагаемые, содержащие базисные перемен­ные x₁, x₂, ..., x_r:

Решение этой системы находится обратным ходом метода; те­перь базисные неизвестные зависят от свободных неизвестных, которые могут принимать любые значения, а потому система (15.1) имеет бесчисленное множество решений.

Рассмотрим примеры решения систем линейных уравнений методом Гаусса.