8. Ранг матрицы

Рангом матрицы А обозначается r(А)= rang(А) называется число не нулевых строк диагональной матрицы

Свойства ранга матрицы:

1. Если матрица А имеет размер m*n то ранг матрицы не превышает наименьшее из чисел m,n.

2. Ранг матрицы А=0 тогда и только тогда когда все элементы А=0 r(А)=0

3. Если А квадратичная порядка n то ранг =n, тогда и только тогда когда определ. матрицы 0

9. Определители второго и третьего порядков. Способы их вычисления.

Понятие определителя

Любой квадратной матрице А порядка n ставится в соот­ветствие по определенному закону некоторое число, называе­мое определителем, или детерминантом, n-го порядка этой матрицы. Начнем с определителей второго и третьего поряд­ков.

Пусть дана матрица

тогда ее определитель второго порядка вычисляется по фор­муле

Правило вычисления определителя второго порядка очевидно: из произведения элементов на главной диагонали вычитает­ся произведение элементов на второй диагонали матрицы А. Нетрудно видеть, что формула (14.1) представляет собой ал­гебраическую сумму двух попарных произведений элементов матрицы А, стоящих в разных строках и разных столбцах.

В дальнейшем мы не будем приводить матрицу, для кото­рой вычисляется определитель, так как в записи определителя содержатся все элементы соответствующей матрицы.

Определитель третьего порядка вычисляется по формуле

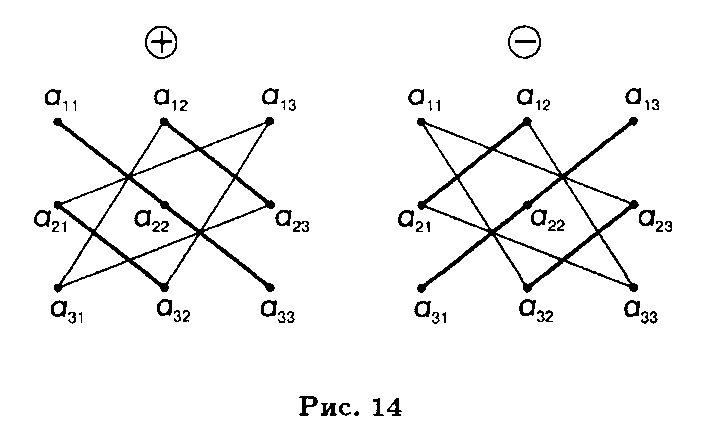
Правило вычисления определителя третьего порядка следу­ющее. Это алгебраическая сумма шести тройных произведе­ний элементов, стоящих в разных строках и разных столб­цах; со знаком плюс берутся произведения, сомножители кото­рых находятся на главной диагонали и в вершинах треугольников, чьи основания параллельны главной диагонали; со зна­ком минус — произведения, сомножители которых стоят на не главной диагонали и в вершинах треугольников с основани­ями, параллельными этой диагонали (рис. 14). Заметим, что каждое слагаемое в формуле (14.2) содержит по одному эле­менту из каждой строки и каждого столбца соответствующей матрицы.

10. Миноры и алгебраические дополнения. Определитель п-го порядка. Разложение определителя по элементам ряда.

Рассмотрим определитель n-го порядка

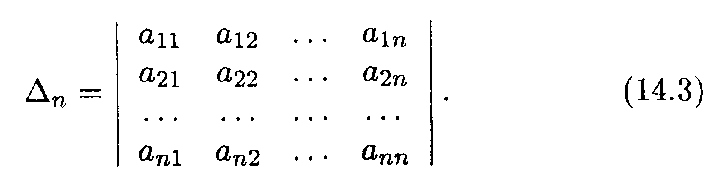
Теперь с учетом подмеченных выше закономерностей перейдем к определению для общего случая.

Определение 1. Определителем матрицы А n-го порядка на­зывается алгебраическая сумма n! произведений n-го порядка элементов этой матрицы, причем в каждое произведение вхо­дит по одному элементу из каждой строки и каждого столбца данной матрицы.

Миноры и алгебраические дополнения

Рассмотрим определитель n-го порядка (14.3). Выделим в нем какой-либо элемент а_ij и вычеркнем i-ю строку и j-й стол­бец, на пересечении которых расположен этот элемент. Полу­ченный определитель (n - 1)-го порядка называется минором M_ij элемента a_ij определителя Δ_n.

Пример 1. Найти минор М₃₂ определителя четвертого по­рядка

Решение. Минор М₃₂ элемента a₃₂ получается вычеркива­нием из данного определителя 3-й строки и 2-го столбца. По­лученный определитель 3-го порядка равен

Определение 2. Алгебраическим дополнением элемента a_ij определителя (14.3) называется число

Так, для приведенного выше примера алгебраическое до­полнение равно

Миноры и алгебраические дополнения играют важную роль в алгебре и ее приложениях. Одним из таких применений яв­ляется основополагающая теорема о способе вычисления опре­делителей.

ТЕОРЕМА 1. Определитель равен сумме произведений эле­ментов любой строки на их алгебраические дополнения:

Формула (14.4) называется разложением определителя по i-й строке. Доказательство этой теоремы мы опускаем. Анало­гичное утверждение имеет место и для разложения определи­теля по любому столбцу.

Формула (14.4) сводит вычисление определителя n-го по­рядка к вычислению n определителей (n - 1)-го порядка. Зная формулу (14.2) вычисления определителя 3-го порядка, мы, на­пример, можем найти определитель 4-го порядка путем разло­жения его на сумму алгебраических дополнений по формуле (14.4).

Пример 2. Вычислить определитель 4-го порядка

Решение. В принципе, разложить определитель можно по любой строке (столбцу), согласно формуле (14.4). Однако объ­ем вычислений можно существенно уменьшить, если выбрать такую строку (столбец), в которой побольше элементов равно нулю. Наиболее подходящей в нашем случае является вторая строка. Разложение по ней определителя имеет вил