7.Транспонирование матриц

Транспонированием матрицы называется замена строк матрицы на ее столбцы с сохранением их порядка (или, что то же самое, замена столбцов матрицы на ее строки). Пусть дана исходная матрица А:

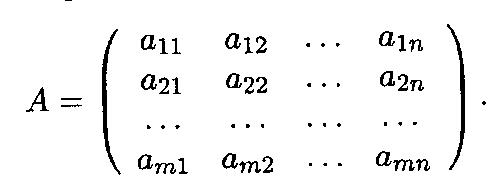
Тогда, согласно определению, транспонированная матрица А' имеет вид

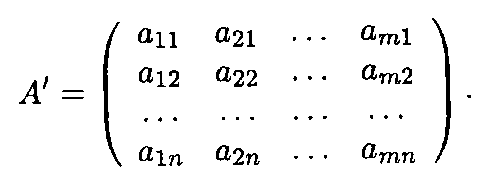
Сокращенная форма записи операции транспонирования мат­рицы:

Пример 3. Пусть даны матрицы А и В:

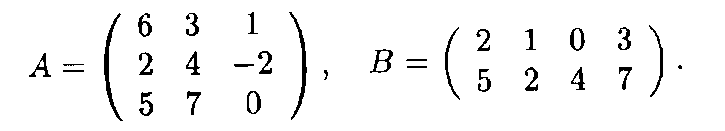
Тогда соответствующие транспонированные матрицы имеют вид

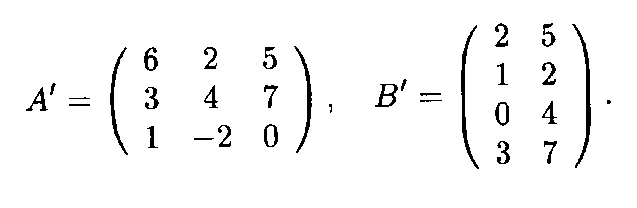
Нетрудно заметить две закономерности операции транспо­нирования матриц.

1. Дважды транспонированная матрица равна исходной матрице:

2. При транспонировании квадратных матриц элементы, находящиеся на главной диагонали, не меняют своих позиций, т.е. главная диагональ квадратной матрицы не меняется при транспонировании.

Важную роль в алгебре и ее приложениях играют симмет­рические матрицы — квадратные матрицы, у которых элемен­ты, симметричные относительно главной диагонали, равны, т.е. a_ij = a_ji. Транспонирование таких матриц не меняет их вида, так что равенство

также можно полагать определением симметрической мат­рицы.

Умножение матриц

1. Умножение матриц — это специфическая операция, со­ставляющая основу алгебры матриц. Строки и столбцы мат­риц можно рассматривать как векторы-строки и векторы-стол­бцы соответствующих размерностей: иными словами, любую матрицу можно интерпретировать как совокупность векторов-строк или векторов-столбцов.

Пусть даны матрица А размером т х п и матрица В разме­ром п х k. Будем рассматривать матрицу А как совокупность т векторов-строк 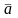_i размерности п каждый, а матрицу В — как совокупность k векторов-столбцов 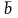_j, каждый из которых содержит по п координат:

Векторы-строки матрицы А и векторы-столбцы матрицы В показаны в записи этих матриц (13.3). Длина строки матри­цы А равна высоте столбца матрицы В, и потому скалярное произведение этих векторов имеет смысл.

Определение 3. Произведением матриц А и В называется матрица С, элементы которой c_ij равны скалярным произве­дениям векторов-строк _i матрицы А на векторы-столбцы _j матрицы В:

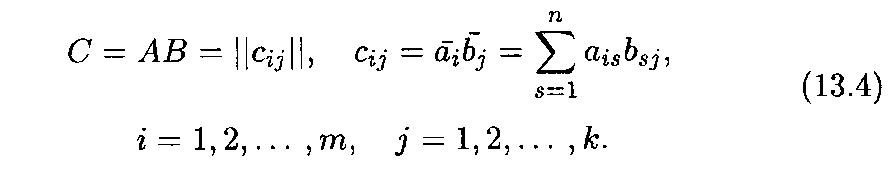
Произведение матриц А и В — матрица С — имеет размер т х k, поскольку длина п векторов-строк и векторов-столбцов исчезает при суммировании произведений координат этих век­торов в их скалярных произведениях, как показано в формулах (13.4). Таким образом, для вычисления элементов первой строки матрицы С необходимо последовательно получить скаляр­ные произведения первой строки матрицы А на все столбцы матрицы В; вторая строка матрицы С получается как ска­лярные произведения второй вектор-строки матрицы А на все векторы-столбцы матрицы В и так далее. Для удобства за­поминания размера произведения матриц нужно перемножить отношения размеров матриц-сомножителей: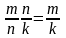 , т.е. размер матрицы С равен произведению оставшихся в отношении чисел: т х k.

В операции умножения матриц есть характерная особен­ность: произведение матриц А и В имеет смысл, если число столбцов в А равно числу строк в В. Тогда если А и В — прямоугольные матрицы, то произведение В и А уже не будет иметь смысла, так как в скалярных произведениях, формиру­ющих элементы соответствующей матрицы, должны участво­вать векторы с одинаковым числом координат.

Если матрицы А и В квадратные размером n х n, то име­ет смысл как произведение матриц АВ, так и произведение матриц BA, причем размер этих матриц такой же, как и у ис­ходных сомножителей. При этом в общем случае перемноже­ния матриц правило перестановочности не соблюдается, т.е. АВ ≠ ВА.

Рассмотрим примеры на умножение матриц.

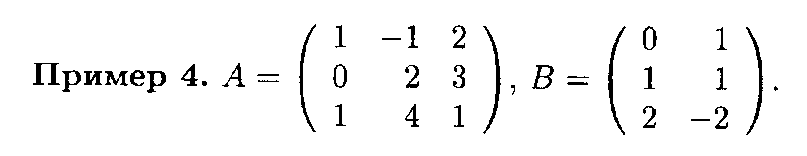
Решение. Поскольку число столбцов матрицы А равно числу строк матрицы В, то произведение матриц АВ имеет смысл. По формулам (13.4) получаем в произведении матрицу размером 3 х 2:

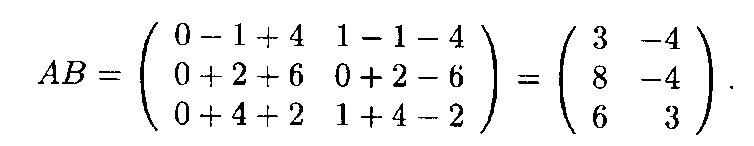
Произведение ВА не имеет смысла, так как число столбцов матрицы В не совпадает с числом строк матрицы А.