5.Угол между векторами. Условие перпендикулярности векторов. Условие коллинеарности векторов.

Определение. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.

рис.1.

Обозначение. . Из определения следует, что .

Мы полагаем очевидным, что при параллельном переносе любого из двух векторов угол между ними остается неизменным, только в этом случае поворот одного из векторов осуществляется либо в общей для обоих векторов плоскости, либо в плоскости параллельной другому вектору.

Условие перпендикулярности векторов:

Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.

Даны два вектора a(xa;ya) и b(xb;yb). Эти векторы будут перпендикулярны, если выражение xaxb + yayb = 0.

Условие коллинеарности векторов:

Векторы коллинеарны, если абсцисса первого вектора относится к абсциссе второго так же, как ордината первого — к ординате второго.

Даны два вектора a(xa;ya) и b(xb;yb). Эти векторы коллинеарны, если xa = xb и ya = yb, где R.

6.Матрицы и операции над ними

Понятие матрицы

Определение 1. Прямоугольная таблица чисел вида

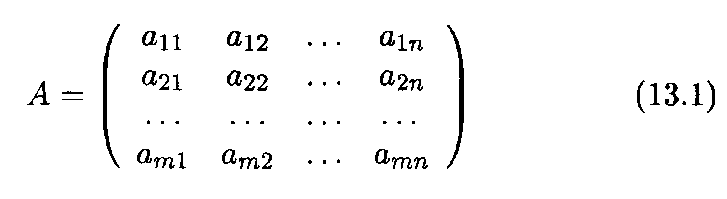
называется матрицей. Здесь a_ij — действительные числа (i = 1, 2,..., m, j = 1, 2, ..., n), называемые элементами матрицы, i и j — соответственно индексы строки и столбца. При этом произведение m х n числа строк на число столбцов называют размером матрицы А. Часто матрицу (13.1) запи­сывают в сокращенном виде

Матрица, все элементы которой равны нулю, называется нулевой матрицей.

В том случае, когда m = n (число строк равно числу столб­цов):

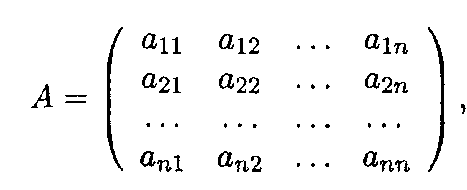
матрица А называется квадратной.

Упорядоченная совокупность элементов a₁₁, a₂₂,. …, а_пп на­зывается главной диагональю квадратной матрицы. Квадрат­ная матрица называется диагональной, если ее элементы удов­летворяют условию

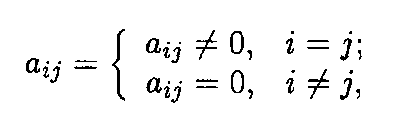
т.е. ненулевыми могут быть только элементы главной диагонали; матрица в этом случае имеет вид

Единичной матрицей называется диагональная матрица, у которой все элементы главной диагонали равны единице:

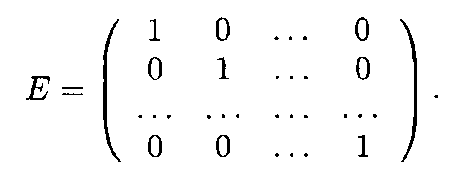
Определение 2. Две матрицы А и В называются равными (А = В), если они имеют одинаковые размеры и их соответ­ствующие элементы равны: a_ij = b_ij , i = 1, 2,..., m, j = 1, 2, .... n.

Линейные операции над матрицами

1. Сумма матриц. Суммой матриц А и В одинакового раз­мера называется матрица С того же размера, каждый элемент которой равен сумме соответствующих элементов матриц А и В. Представим это в сокращенной записи. Пусть

Тогда сумма этих матриц С = А + В имеет вид

Пример 1. Пусть даны матрицы А и В:

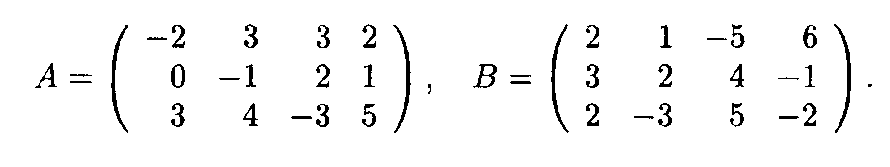
Тогда их суммой, согласно определению, является матрица

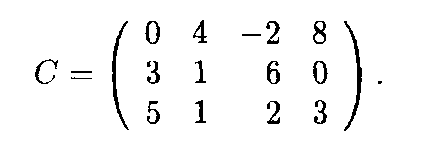
2. Умножение матрицы на действительное число. Произ­ведением матрицы А на действительное число α называется матрица, каждый элемент которой получен умножением соот­ветствующего элемента матрицы А на число α.