
Билет15
Идеальный
газ
— математическая
модель
газа,
в которой предполагается, что потенциальной
энергией молекул
можно пренебречь по сравнению с их
кинетической энергией. Между молекулами
не действуют силы притяжения или
отталкивания, соударения частиц между
собой и со стенками сосуда абсолютно
упруги,
а время взаимодействия между молекулами
пренебрежимо мало по сравнению со
средним временем между столкновениями.
Уравнение
состояния
идеального
газа
(иногда уравнение
Клапейрона
или уравнение
Клапейрона
— Менделеева) —
формула, устанавливающая зависимость
между давлением,
молярным
объёмом
и абсолютной
температурой
идеального
газа.
Уравнение имеет вид:![]() где
где![]() —
давление,
—
давление,![]() —
молярный
объём,
—
молярный
объём,![]() —
универсальная
газовая постоянная
—
универсальная
газовая постоянная![]() —
абсолютная
температура,К
—
абсолютная
температура,К
Так как
![]() ,
где
,
где
![]() —
количество
вещества,
а
—
количество
вещества,
а
![]() ,
где
,
где
![]() —
масса,
—
масса,
![]() —
молярная
масса,
уравнение состояния можно записать:
—
молярная
масса,
уравнение состояния можно записать:![]()
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.
В случае постоянной
массы газа уравнение можно записать в
виде:![]()
![]() Закон Дальтона для смеси газов
Закон Дальтона для смеси газов
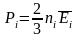 Пусть
есть смесь нескольких идеальных газов.
Для каждого газа можно записать уравнение,
где ni
– концентрация молекул i-го
газа, Рi
– парциальное давление этого газа
(давление при мысленном удалении из
сосуда молекул других газов). Поскольку
давление на стенку сосуда обусловлено
ударами о нее молекул, то общее давление
смеси идеальных газов равно сумме
парциальных давлений отдельных газов:
Пусть
есть смесь нескольких идеальных газов.
Для каждого газа можно записать уравнение,
где ni
– концентрация молекул i-го
газа, Рi
– парциальное давление этого газа
(давление при мысленном удалении из
сосуда молекул других газов). Поскольку
давление на стенку сосуда обусловлено
ударами о нее молекул, то общее давление
смеси идеальных газов равно сумме
парциальных давлений отдельных газов:
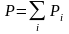 -
закон Дальтона.В смеси нескольких
идеальных газов уравнения состояния
справедливы для каждого газа в отдельности,
причем объем V
и температура Т
у всех газов одинаковы, а парциальные
давления отдельных газов и общее давление
в смеси связаны законом Дальтона.
-
закон Дальтона.В смеси нескольких
идеальных газов уравнения состояния
справедливы для каждого газа в отдельности,
причем объем V
и температура Т
у всех газов одинаковы, а парциальные
давления отдельных газов и общее давление
в смеси связаны законом Дальтона.
Покажем, что для
смеси идеальных газов общее давление
Р,
объем V,
температура Т
и суммарное число молей v
связаны равенством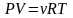 ,
,
которое внешне
совпадает с равенством (6) для одного
газа. Запишем уравнение состояния для
каждого сорта газа:
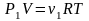
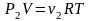
Билет 16
Молекулярно-кинетическая
теория (сокращённо МКТ) — теория XIX
века, рассматривавшая строение вещества,
в основном газов, с точки зрения трёх
основных приближенно верных положений:все
тела состоят из частиц, размером которых
можно пренебречь: атомов,
молекул
и ионов;частицы
находятся в непрерывном хаотическом
движении (тепловом);частицы взаимодействуют
друг с другом путём абсолютно
упругих столкновений.Основными
доказательствами этих положений
считались:Диффузия,Броуновское
движение,Изменение
агрегатных
состояний
вещества![]() ,
где k
является постоянной
Больцмана
(отношение Универсальной
газовой постоянной
R
к числу
Авогадро
NA),
а i —
число степеней свободы молекул.Основное
уравнение МКТ связывает макроскопические
параметры (давление,
объём,
температура)
газовой системы с микроскопическими
(масса молекул, средняя скорость их
движения). Вывод
основного уравнения МКТ
,
где k
является постоянной
Больцмана
(отношение Универсальной
газовой постоянной
R
к числу
Авогадро
NA),
а i —
число степеней свободы молекул.Основное
уравнение МКТ связывает макроскопические
параметры (давление,
объём,
температура)
газовой системы с микроскопическими
(масса молекул, средняя скорость их
движения). Вывод
основного уравнения МКТ
Пусть имеется кубический сосуд с ребром длиной l и одна частица массой m в нём.
Обозначим скорость
движения vx,
тогда перед столкновением со стенкой
сосуда импульс
частицы равен mvx,
а после — − mvx,
поэтому стенке передается импульс p
= 2mvx.
Время, через которое частица сталкивается
с одной и той же стенкой, равно
![]() .Отсюда
следует:
.Отсюда
следует:![]() Так
как давление
Так
как давление
![]() ,
следовательно сила F
= p
* SПодставив,
получим:
,
следовательно сила F
= p
* SПодставив,
получим:
![]() Преобразовав:
Преобразовав:
![]() Так
как рассматривается кубический сосуд,
то V
= SlОтсюда:
Так
как рассматривается кубический сосуд,
то V
= SlОтсюда:![]() .Соответственно,
.Соответственно,
![]() и
и
![]() .Таким
образом, для большого числа частиц верно
следующее:
.Таким
образом, для большого числа частиц верно
следующее:
![]() ,
аналогично для осей y и z.Поскольку
,
аналогично для осей y и z.Поскольку
![]() ,
то
,
то
![]() .
Это следует из того, что все направления
движения молекул
в хаотичной среде равновероятны.Отсюда
.
Это следует из того, что все направления
движения молекул
в хаотичной среде равновероятны.Отсюда
![]() или
или
![]() .Пусть
.Пусть
![]() —
среднее значение кинетической энергии
всех молекул, тогда:
—
среднее значение кинетической энергии
всех молекул, тогда:
![]() ,
откуда
,
откуда
![]() .Для
одного моля выражение примет вид
.Для
одного моля выражение примет вид
![]()
