14.Электроёмкость. Соединение конденсаторов. Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.

В системе СИ ёмкость измеряется в фарадах.

При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы, так как от источника питания они поступают только на внешние электроды, а на внутренних электродах они получаются только за счёт разделения зарядов, ранее нейтрализовавших друг друга. Общая ёмкость батареи последовательно соединённых конденсаторов равна

15.Расчёт электроцепи методом контурных токов. Если в схеме присутствует источник напряжения управляемый напряжением (ИНУН) то для этой схемы можно составить уравнения методом контурных токов и найти токи во всех ветвях. Метод контурных токов можно применить для расчета сложных электриче­ских цепей, имеющих больше двух узловых точек. На рис. 41, а изображена такая электрическая цепь. В ней три контура, причем средний контур имеет участки, входящие в состав двух соседних контуров, а также участки, которые входят в состав только одного контура.

Сущность метода контурных токов заключается в предположении, что в ка­ждом контуре проходит свой ток (контурный ток). Тогда на общих участках, расположенных на границе двух соседних контуров, будет протекать ток, равный алгебраической сумме токов этих контуров.

16.Расчёт электроцепи методом двух узлов.

Метод двух узлов — метод расчета электрических цепей, в котором за искомое (с его помощью определяют затем и токи ветвей) принимают напряжение между двумя узлами схемы.

Часто встречаются схемы, содержащие всего два узла. Наиболее рациональным методом расчета токов в них является метод двух узлов.

17.Характеристики магнитного поля.

Основными характеристиками магнитного поля являются магнитная индукция, магнитный поток, магнитная проницаемость и напряженность магнитного поля. Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле. 18.Электромагнитная индукция. Самоиндукция. Взаимоиндукция. Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. Закон Фарадея

Согласно закону электромагнитной индукции Фарадея (в СИ):

где

 — электродвижущая сила, действующая вдоль произвольно выбранного контура,

   — магнитный поток через поверхность, натянутую на этот контур.

Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре^[1] при изменении тока, протекающего по контуру.

При изменении тока в контуре пропорционально меняется^[2] и магнитный поток через поверхность, ограниченную этим контуром^[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока  :

.

Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитной индукции. При изменении тока в одном из проводников или при изменении взаимного расположения проводников происходит изменение магнитного потока через (воображаемую) поверхность, "натянутую" на контур второго, созданного магнитным полем, порожденным током в первом проводнике, что по закону электромагнитной индукции вызывает возникновение ЭДС во втором проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. 19.Способы представления синусоидальных величин.  Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ. Электрический ток. Плотность тока. Электрическое напряжение.

Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, - периодом Т. Для периодического тока имеем

,

(2)

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота  f = 50Гц.

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i  - мгновенное значение тока  ;

е- мгновенное значение ЭДС   .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексомm).

  - амплитуда напряжения;

20. Закон Ома и Кирхгофа в символической форме записи Закон Ома для всей цепи выражает соотношение между электродвижущей силой (ЭДС), сопротивлением и током. Согласно этому закону ток в замкнутой цепи равен ЭДС источника деленной на сопротивление всей цепи:

 

,                                                  (1.19)

где I - ток, протекающий по цепи;

E - ЭДС, генератора, подключенного к электрической цепи;

Rг - сопротивление генератора;

Rц - сопротивление цепи.

Закон Ома для участка цепи. Ток на участке цепи прямо пропорционален напряжению между началом и концом  участка и обратно пропорционален сопротивлению участка. Аналитически закон выражается в следующем виде:

,                                                                  (1.20)

где I - ток, протекающий на участке цепи;

R - сопротивление участка цепи;

U - напряжение на участке цепи.

Обобщенный закон Ома. Сила тока  в контуре цепи прямо пропорциональна алгебраической сумме ЭДС всех источников цепи и обратно пропорциональна арифметической сумме всех активных сопротивлений цепи.

,                                                          (1.21)

где m и n – количество источников и резисторов в контуре цепи.

При алгебраическом суммировании со знаком “плюс” берутся те ЭДС, направление которых совпадает с направлением тока, а со знаком “минус”– те ЭДС, направление которых не совпадает с направлением тока.

Первый закон Кирхгофа. Электрические цепи подразделяют на неразветвленные и разветвленные. На рис. 1.10 представлена простейшая разветвленная цепь.

Рис. 1.10 Схема разветвленной цепи.

Разветвленной называется такая электрическая цепь, в которой ток от какого-либо источника может идти по различным путям и, в которой, следовательно, имеются точки, где сходятся два и более проводников. Эти точки называют узлами. Токи, текущие к узлу считаются имеющими один знак, а от узла – другой.

Учитывая это правило для схемы, изображенной на рис. 1.11,а можно записать

 или

.

21. Основные параметры переменного тока При подключении к источнику переменного тока с синусоидально изменяющейся э. д. с. электрических цепей с линейными сопротивлениями в них будут действовать синусоидально изменяющиеся напряжения и проходить синусоидально изменяющиеся токи. Переменные токи, э. д. с. и напряжения характеризуются четырьмя основными параметрами: периодом, частотой, амплитудой и действующим значением.

Период. Промежуток времени Т, в течение которого э. д. с, напряжение и или ток i (рис. 169, а) совершают полный цикл изменений, называется периодом. Чем быстрее вращается виток или ротор генератора переменного тока, тем меньше период изменения э. д. с. или тока.

Частота. Число полных периодов изменения э. д. с, напряжения или тока в 1 с называется частотой,

f = 1 / T

Она измеряется в герцах (Гц), т. е. числом периодов в секунду. Чем больше частота, тем меньше период изменения тока, напряжения или э. д. с. (рис. 169,б). В Советском Союзе все электрические станции переменного тока вырабатывают ток, изменяющийся с частотой 50 Гц, т. е. 50 периодов в секунду. В автоматике и радиотехнике применяют электрические токи и более высоких частот. Такие частоты измеряются в килогерцах (1 кГц=10³ Гц) и мегагерцах (1 МГц=10⁶ Гц).

Рис. 169. Кривые изменения синусоидального переменного тока при различной частоте

Из рис. 169,а следует, что в течение времени одного периода Т фаза ?t тока (э. д. с. или напряжения) изменяется на угол 360°, или 2? радиан. Поэтому

? = 2?/T = 2?f

Эту величину называют угловой частотой переменного тока, она имеет размерность рад/с.

Амплитуда. Наибольшее значение переменного тока (переменных э. д. с. и напряжения) называют амплитудным значением, или амплитудой. В рассмотренном нами простейшем генераторе переменного тока (см. рис. 168, а) э. д. с. е дважды достигает амплитудного значения: во время первого полуоборота +Е_т (направлена от начала витка к его концу), а во время второго полуоборота — Е_т (направлена от конца витка к его началу). Точно так же за один период ток i 2 раза достигает амплитудного значения: I_т и — I_т. Амплитудное значение тока, напряжения и э. д. с. в формулах обозначают соответствующими буквами с индексами «т», т. е. I_т U_т, Е_т и др.

Действующее значение. Ток, напряжение и э. д. с, действующие в электрической цепи в каждый отдельный момент времени, определяются так называемыми мгновенными значениями. Эти значения принято обозначать строчными буквами i, и, е. Однако судить о переменных э. д. с, токе или напряжении по их мгновенным значениям неудобно, так как эти значения непрерывно меняются. Поэтому оценивать способность переменного тока совершать механическую работу или создавать тепло принято по действующему его значению. Под действующим значением переменного тока понимают силу такого постоянного тока (прямая 2 на рис. 169,а), который, проходя по проводнику в течение некоторого времени (например, в течение одного периода или 1 с), выделит в нем такое же количество тепла (произведет такую же механическую работу), как и данный переменный ток (кривая 1). Действующие значения тока, напряжения и э. д. с. обозначают соответственно I, U, Е.

22. Переменный синусоидальный ток. Параметры. Действующее среднее значение Синусоидальным током называют ток, изменяющийся во времени по синусоидальному закону (рис. 2.1):

 

Ток  i(t)  называют мгновенным. Максимальное значение тока называют амплитудой и обозначают   . Период   – это время, за которое совершается одно полное колебание. Частота равна числу колебаний в секунду  , единица частоты   - герц (Гц).

Угловая частота  , единица угловой частоты рад/с или  . Аргумент синуса, т.е.  , называют фазой. Фаза характеризует состояние колебания в данный момент времени  .

Начальная фаза тока -  .

Параметры синусоидального напряжения и тока. Самое широкое применение нашли синусоидальные переменные напряжения и токи:

Временная зависимость синусоидального сигнала

Их временные зависимости характеризуются тремя параметрами:

1. U_м или I_м — амплитуда переменного напряжения или тока;

2. f — частота (число периодов, возможно неполных) в единицу времени;

3. θ — фазовый сдвиг (сдвиг зависимостей  в долях).

Синусоидальные сигналы являются периодическими, т.е. их временная зависимость повторяется, и имеют место условия u(t) = u(t + T) и i(t) = i(t + T), где T = 1/f — период повторения сигнала.

Фазовый сдвиг сигналов напряжения и тока (или входного и выходного напряжений) связан с влиянием реактивных компонентов (L и С) цепей, а также с работой различных фазосдвигающих цепей, например,фазоинверторов и трансформаторов. Фазовый сдвиг измеряется в градусах (360⁰ соответствует сдвигу на период) или в радианах (2π радиан соответствует сдвигу на период).

Поскольку все три параметра синусоидального сигнала неизменны во времени, то такие сигналы (напряжения или токи) называются стационарными. Если осуществляется их изменение во времени (модуляция), то сигналы будут нестационарными (см. рис. выше, б и в). В большинстве случаев речь идет об измерении параметров синусоидальных сигналов или сигналов с медленно изменяющимися во времени параметрами. Это позволяет рассматривать такие сигналы как синусоидальные, хотя это и не совсем так — модулированные сигналы становятся уже не стационарными и не являются строго синусоидальными.

Отсюда получаем, что дей­ствующее значение синусоидаль­ного тока (рис. 132)

23. Нагрузка цепей переменного тока, их характеристика и параметры Активное сопротивление ( r) – нагрузка, аналогичная той, которая использовалась в цепях постоянного тока.

Реактивные сопротивления (X) – нагрузки, которые не использовались в цепях постоянного тока. Они используются только в цепях переменного тока и не потребляют активную мощность.

И ндуктивность

Индуктивность (первый вариант определения) – это свойство физического объекта (катушки) запасать в себе энергию магнитного поля и отдавать её при следующих условиях: если ток и напряжение катушки одного знака, энергия запасается, если же разного знака, то энергия катушкой отдается.

Индуктивность (второй вариант определения) – это коэффициент пропорциональности между потокосцеплением и током, вызвавшем это потокосцепление.

Индуктивность на схемах обозначается буквой L и измеряется в генри (Гн).

Пусть дана катушка (рис. 2.5). Если контур интегрирования (k) направить по силовой линии так, чтобы он охватывал все витки катушки, то закон полного тока при Н = const, можно записать: H k = w i

Магнитная индукция связана с напряженностью: В = m m₀Н, где m – относительная величина, показывающая, во сколько раз проницаемость данной среды больше магнитной проницаемости вакуума; m₀ – магнитная проницаемость вакуума.

Потокосцепление (y) определяется потоком:  , где  .

Если Н = const, то , и индуктивность, как коэффициент пропорциональности между потокосцеплением и током, равна:

Тогда становится очевидным, что L – это параметр, зависящий от числа витков, геометрических размеров катушки и магнитной проницаемости среды.

24. Цепь переменного тока с активной нагрузкой, векторная диаграмма 23. Цепь с идеальной катушкой индуктивности, векторная диаграмма Векторная под буквой В Катушка индуктивности при протекании по ней тока обладает способностью создавать магнитное поле. Это свойство характеризуется параметром катушки, называемым индуктивностью L. Катушка обладает и активным сопротивлением

где ρ – удельное сопротивление материала проводника; l – длина проводника; s – сечение проводника.

Для удобства анализа работы катушки в цепи переменного тока условно будем считать, что R_K = 0 (идеализированная катушка).

Пусть по катушке с числом витков w протекает ток, изменяющийся по закону I = I_m·sinω·t (начальная фаза принята равной нулю). Этот ток создаёт синусоидальный магнитный поток, мгновенное значение которого равно

где Ф_m – амплитуда потока 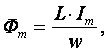  а начальная фаза и частота равны начальной фазе и частоте тока.

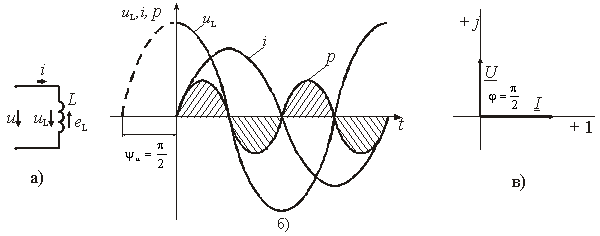
Напряжение источника и = и_L уравновешивается ЭДС самоиндукции е_L катушки

Из выражения видно, что начальная фаза напряжения ψ_u = π/2. Следовательно, синусоида напряжения на идеальной катушке индуктивности опережает синусоиду тока по фазе на угол π/2

φ = ψ_u – ψ_i = π/2 – 0 = π/2.

На практике, если напряжение по фазе опережает ток, говорят об индуктивном характере нагрузки. График мгновенных значений и векторная диаграмма тока и напряжения цепи с индуктивностью приведены на рис. 3.5.

Амплитуда напряжения

U_m = ωLI_m,

откуда имеем

Действующее значение тока равно

Это выражение представляет закон Ома для идеальной индуктивности.

26.Цепь переменного тока с емкостью, векторная диаграмма Ток и напряжение. В цепи постоянного тока емкость (идеальный конденсатор) имеет сопротивление бесконечно большое, так как после окончания процесса заряда такой конденсатор не пропускает электрический ток. Однако при подключении емкости к источнику переменного тока (рис. 191,а) происходит непрерывный процесс его заряда и разряда, при этом через емкость проходит переменный ток.

Ток i при включении в цепь переменного тока емкости определяется количеством электричества q, проходящим по этой цепи в единицу времени. Следовательно,

i = ?q / ?t

где ?q — изменение количества электричества (заряда q) за время ?t.

Количество электричества q, накопленное в конденсаторе при изменении напряжения и, также непрерывно изменяется. Поэтому, учитывая формулу (69), будем иметь:

i = C ?u / ?t

где ?u — изменение напряжения и за время ?t.

Из рис. 191,б видно, что скорость изменения напряжения ?u/?t будет наибольшей в моменты времени, когда угол ?t равен 0; 180 и 360°. Следовательно, в эти моменты времени ток i имеет максимальное значение. В моменты же времени, когда угол ?t равен 90° и 270°, скорость изменения напряжения ?u/?t = 0 и поэтому i = 0.

В течение первой четверти периода происходит заряд емкости и в цепи течет ток заряда, который считаем положительным. При этом по мере заряда емкости и увеличения разности потенциалов на электродах ток i уменьшается. При ?t = 90° емкость полностью заряжается, разность потенциалов на электродах становится равной напряжению и источника и ток i = 0.

Во второй четверти периода емкость начнет разряжаться и ток i изменяет свое направление (становится отрицательным). При

Рис. 191. Схема включения в цепь переменного тока емкости (а), кривые тока i напряжения u (б) и векторная диаграмма (в)

?t =180°, когда u = 0, ток i разряда достигает максимального значения. В этот момент изменяется полярность напряжения и источника и начинается процесс перезаряда емкости при противоположном (отрицательном) направлении тока i. При со/ = 270° заряд прекращается, ток i становится равным нулю и начинается разряд при первоначальном (положительном) направлении тока.

Таким образом, емкость в течение одного периода изменения напряжения и дважды заряжается и дважды разряжается. Следовательно, в цепи (см. рис. 191, а) непрерывно протекает переменный ток i. Из рис. 191,б видно, что при включении в цепь переменного тока емкости ток i опережает по фазе напряжение и на угол 90° или же что напряжение и отстает по фазе от тока i на угол 90° (рис. 191,в).

Емкостное сопротивление. Сопротивление, которое оказывает емкость переменному току, называют емкостным. Оно обозначается X_с и измеряется в омах. Физически емкостное сопротивление обусловлено действием э. д. с. е_с, возникающей в конденсаторе С. Эта э. д. с. направлена против приложенного напряжения u, так как заряженный конденсатор можно рассматривать как источник с некоторой э. д. с. е_с, действующей между его пластинами. Поэтому э. д. с. е_с препятствует изменению тока под действием напряжения u, т. е. оказывает прохождению переменного тока определенное сопротивление.

Из формулы (70) следует, что чем больше емкость С и скорость изменения напряжения ?u/?t, т. е. частота его изменения f (значение ?), тем больше ток i в цепи с емкостью и тем меньше емкостное сопротивление:

X_с = 1 /(?C)

Закон Ома для цепи с емкостью:

I = U / X_с = U / ( 1 /(?C) )

Электрическая мощность. Рассмотрим, как изменяется электрическая мощность в цепи переменного тока с емкостью. Ее можно получить графическим путем, перемножая ординаты кривых тока и напряжения при различных углах ?t. Кривая мгновенной мощности (см. рис. 179,б) представляет собой синусоиду, которая изменяется с двойной частотой 2? по сравнению с частотой изменения тока i и напряжения u. Следовательно, в этой цепи тоже имеет место непрерывный колебательный процесс обмена энергией между источником и емкостью. В первую и третью четверти периода мощность положительна, т. е. конденсатор получает энергию W от источника и накапливает ее в своем электрическом поле. Во вторую и четвертую четверть периода конденсатор отдает накопленную энергию источнику (мощность отрицательна); при этом протекание тока по цепи поддерживается э. д. с. е_с. В целом за период в емкостное сопротивление не поступает электрическая энергия (среднее значение мощности за период равно нулю). Поэтому емкостное сопротивление, так же как и индуктивное, относят к группе реактивных сопротивлений.

Для характеристики процесса обмена энергией между источником и емкостью введено понятиереактивной мощности емкости:

Q_с = U_сI

где U_с — напряжение, приложенное к конденсатору (действующее значение) .

Эту мощность можно выразить также в виде

Q_с = U²_с/ X_с или Q_с = I²X_с

Следует отметить, что в реальных конденсаторах имеют место потери мощности, вследствие чего они потребляют от источника некоторую электрическую энергию. Потери мощности вызваны тем, что в диэлектрике, разделяющем пластины конденсатора, под действием переменного электрического поля возникают токи смещения, нагревающие диэлектрик. Чем больше напряжение и частота его изменения, тем больше потери мощности в конденсаторах от токов смещения. Однако эти потери имеют значение только в конденсаторах, применяемых в высокочастотных установках. При стандартной частоте 50 Гц потери в конденсаторах настолько малы, что их обычно не учитывают.