Лекция № 11.
;
;
;
.
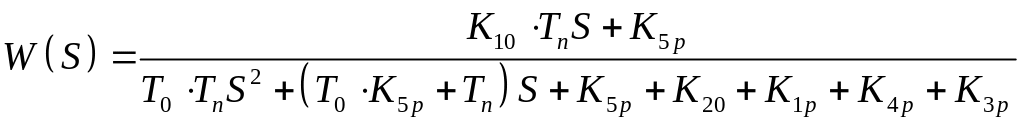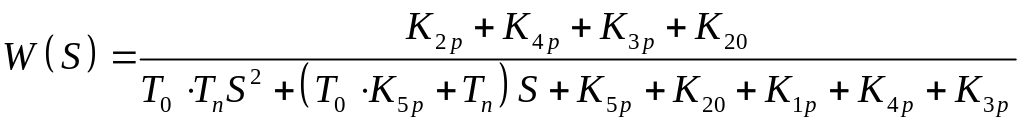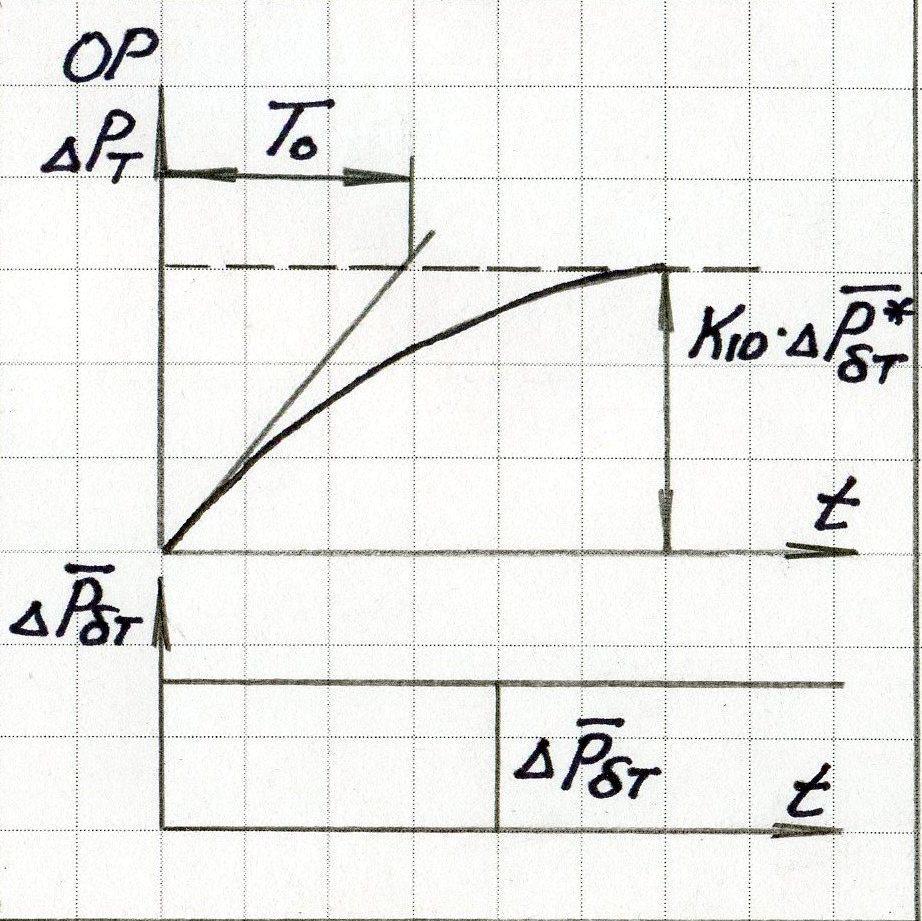
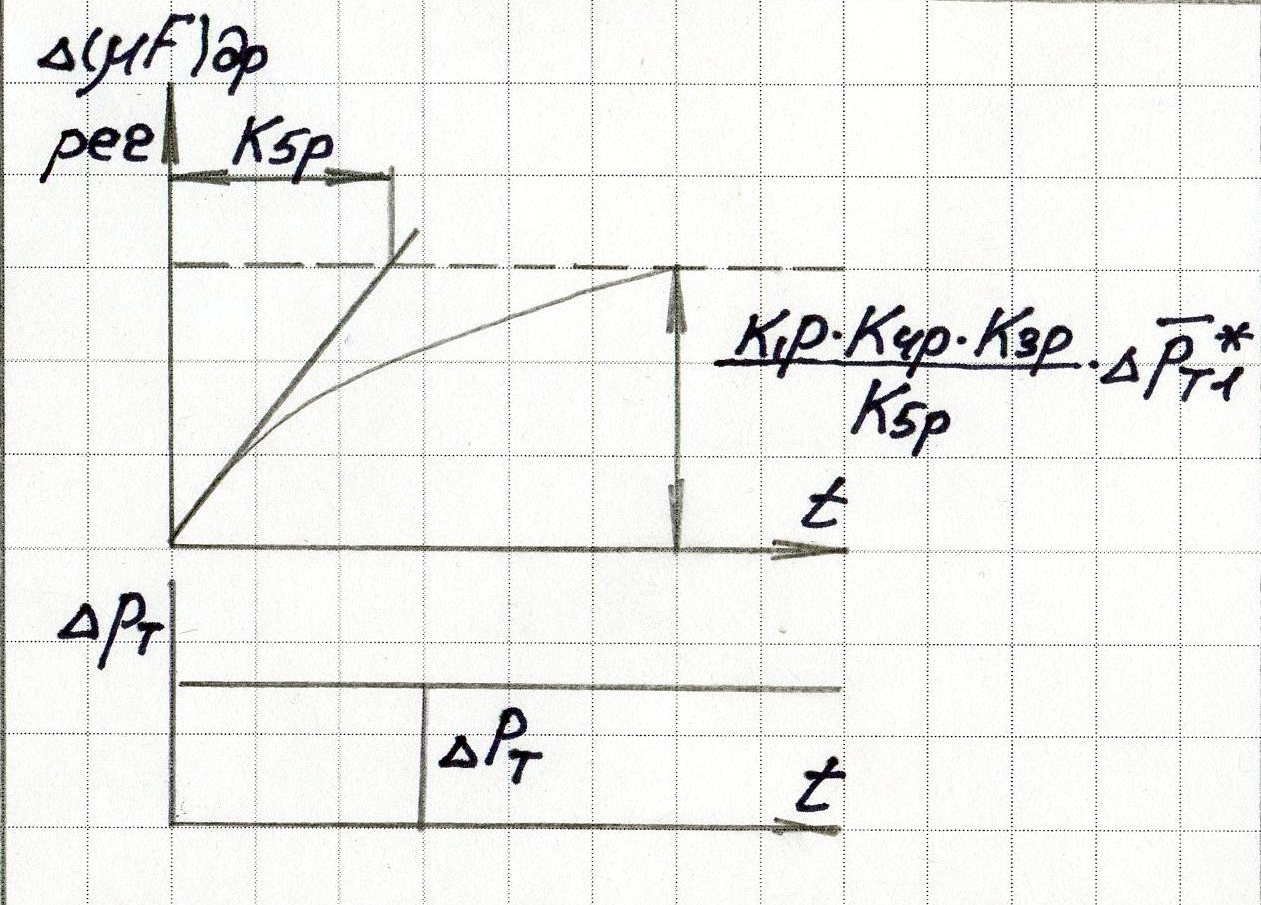
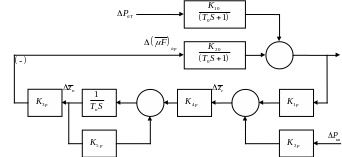
Регулятор:
;
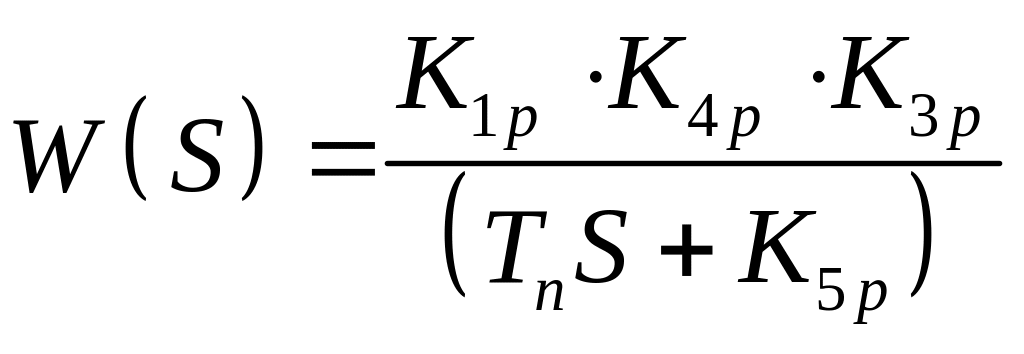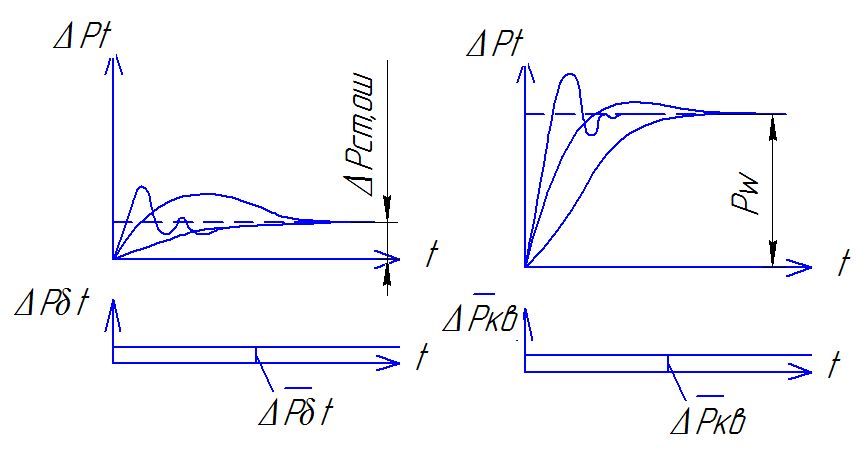
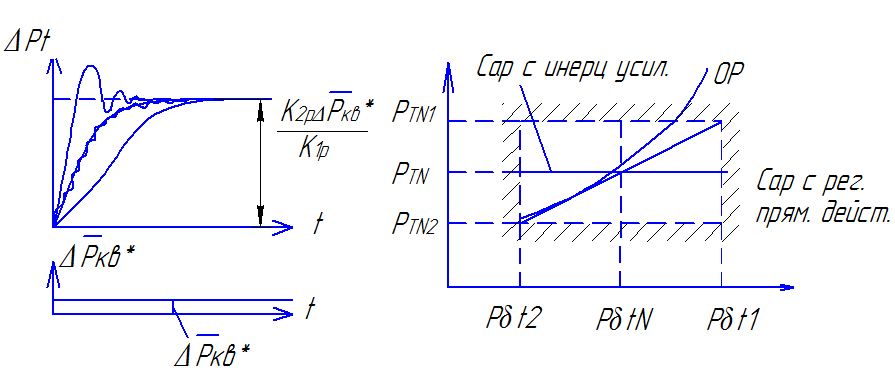
С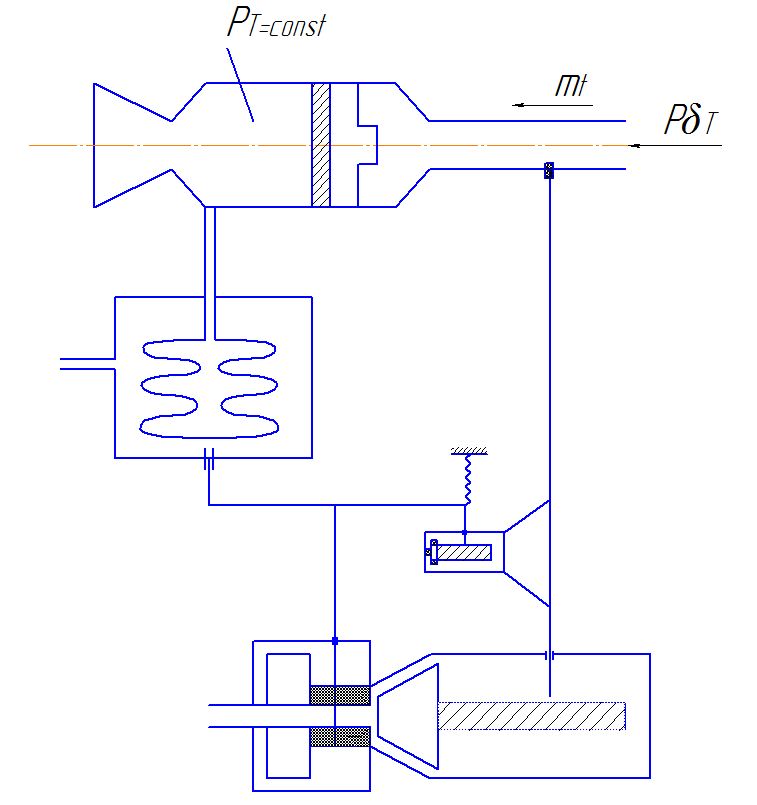
ар
с изодромным регулятором.
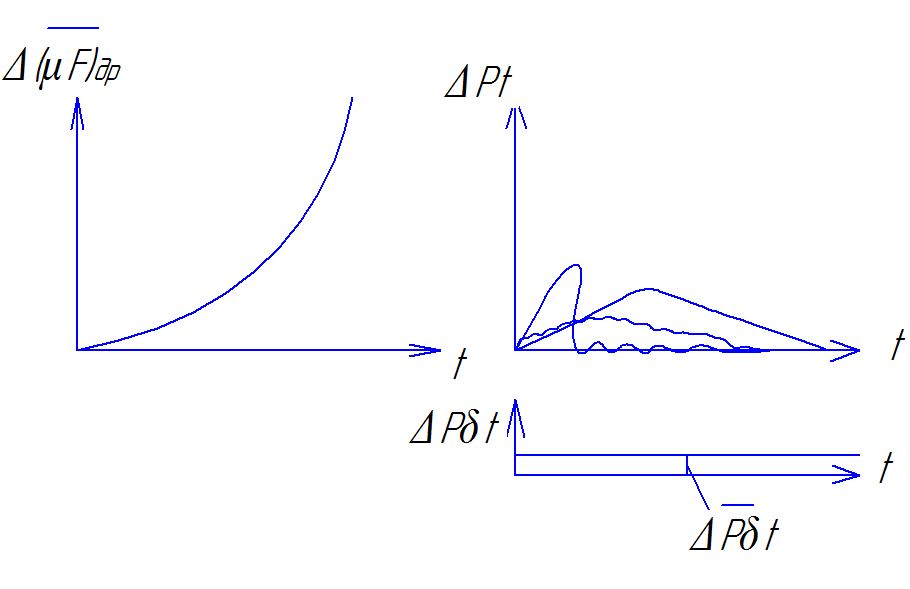
Изодром: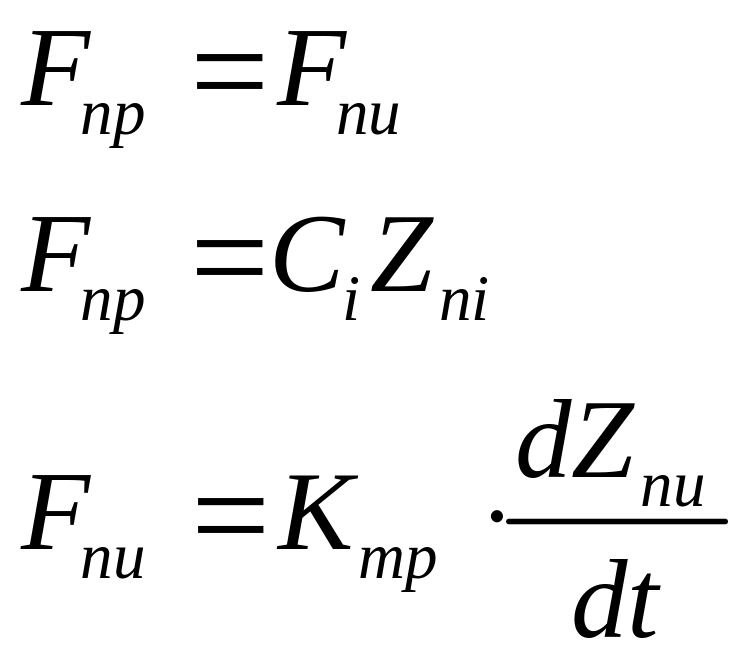
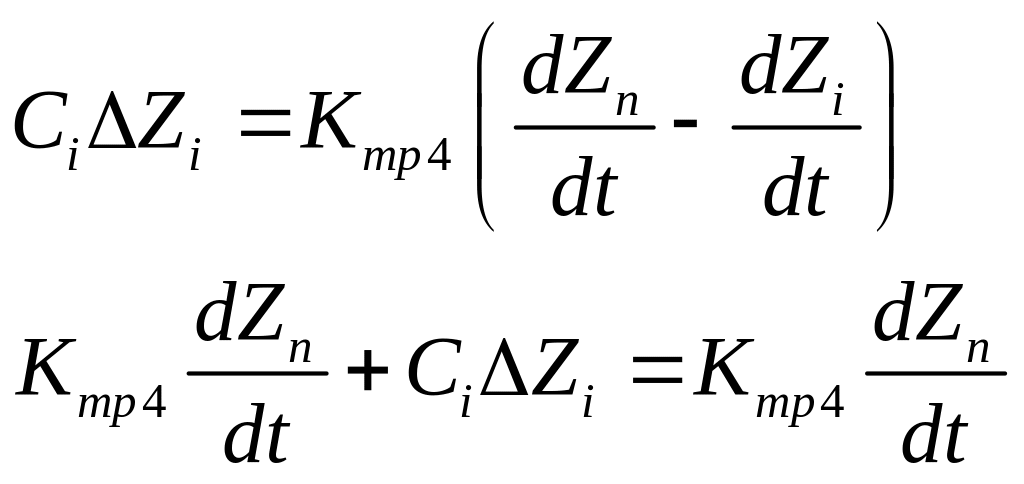
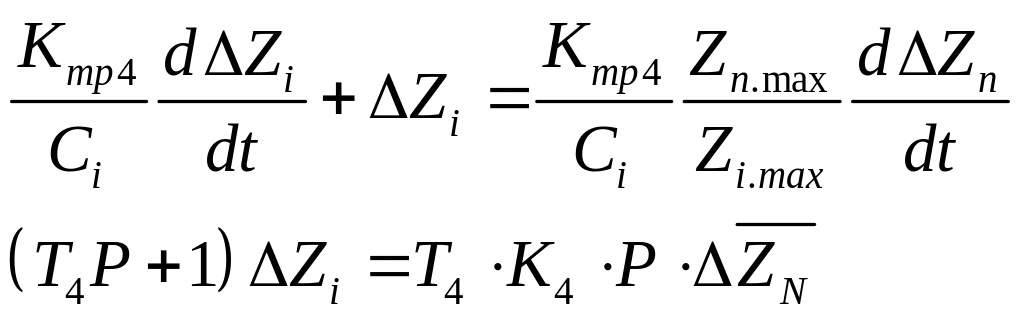
В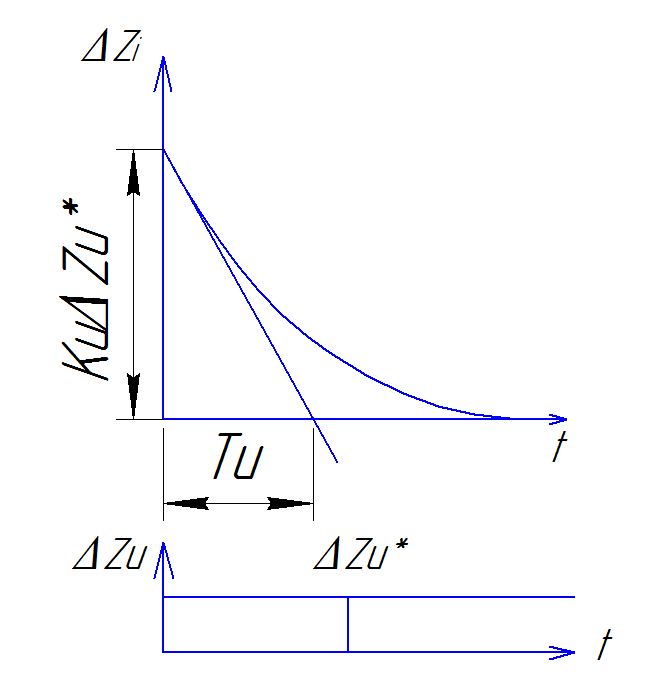
ывод
уравнения динамики по изменению объема
твёрдого топлива.
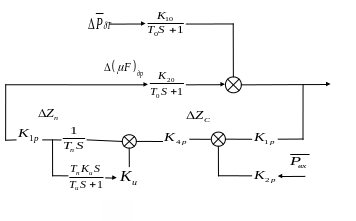
Ор и ЧЭ и дроссель теже и усилитель.
Изодром
Обратная связь
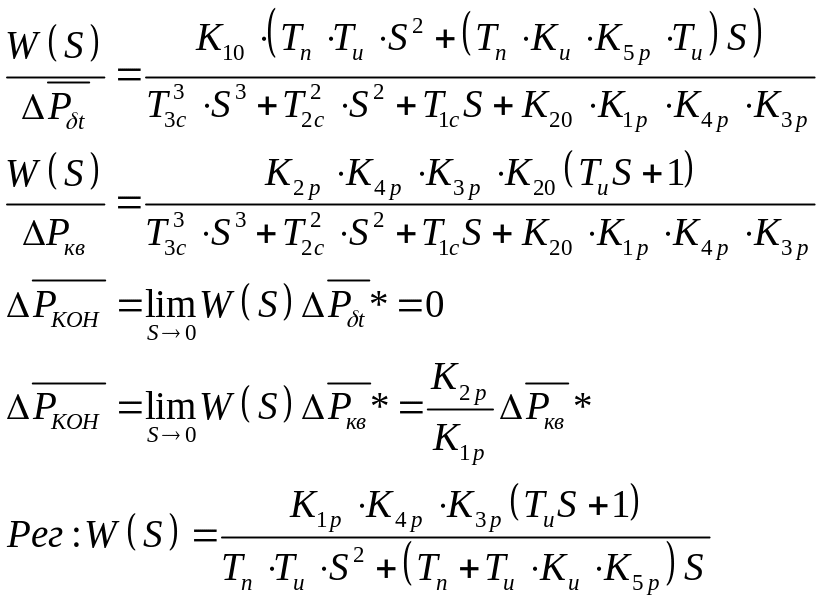
Лекция № 12.
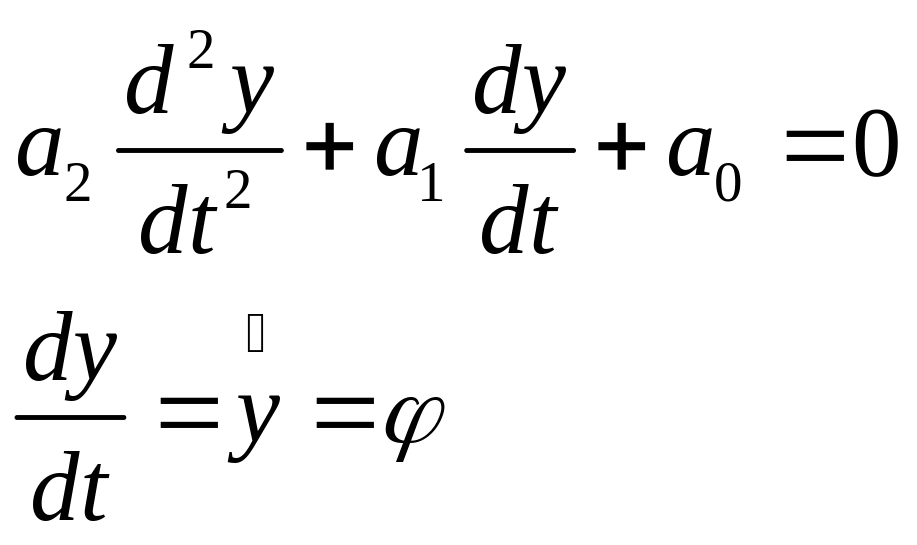
(1)
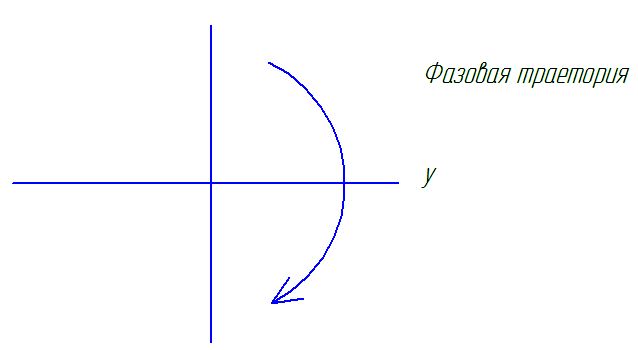
Фазовая плоскость.
Фазовая траектория линейных систем.
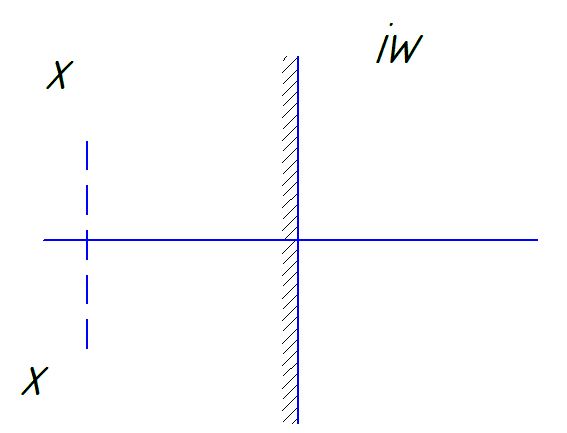избавляемся от
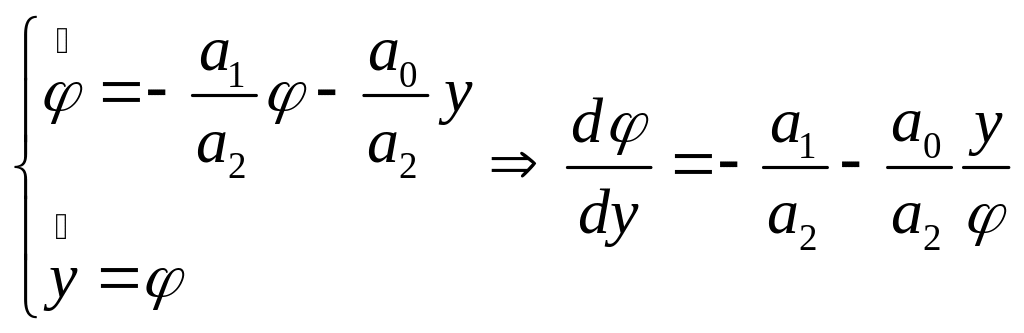(2)
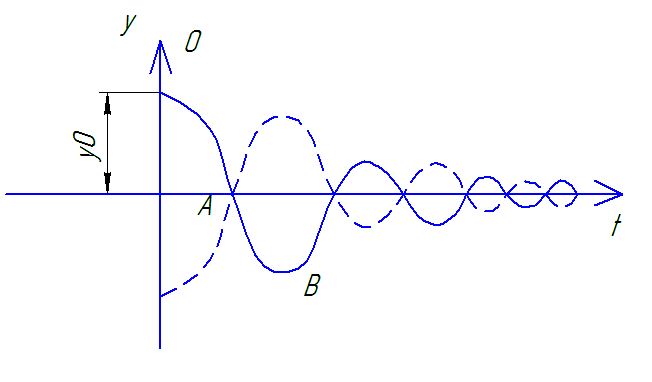
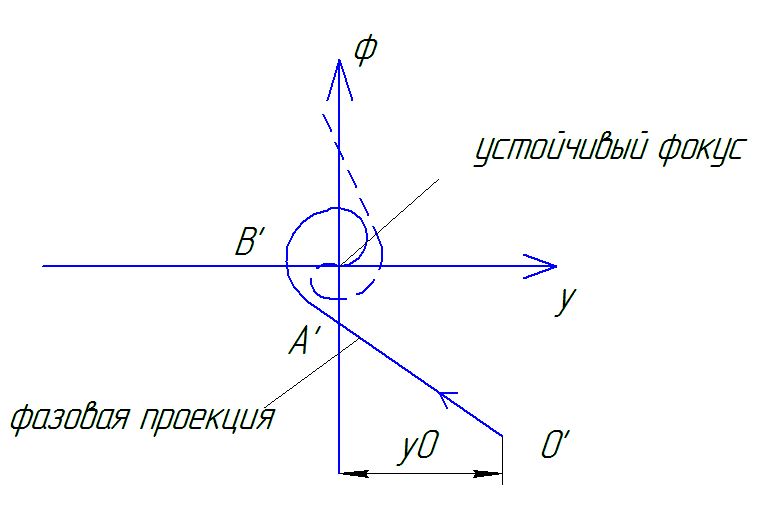
Фазовый портрет
Логарифмическая спираль.
Если есть семейство фазовых траекторий, то можно получить: ( преобразовав 2)
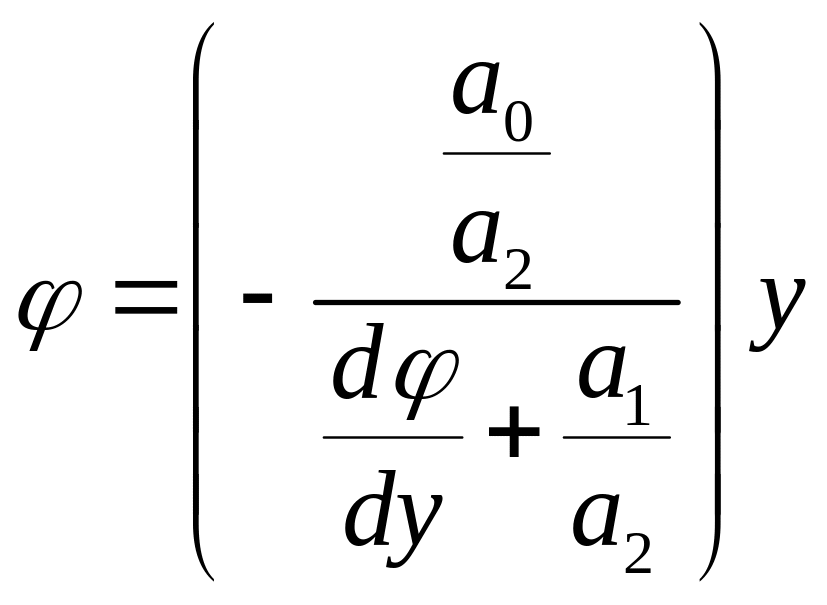изоклина-линия одинакового наклона
касательных к фазовым траекториям.
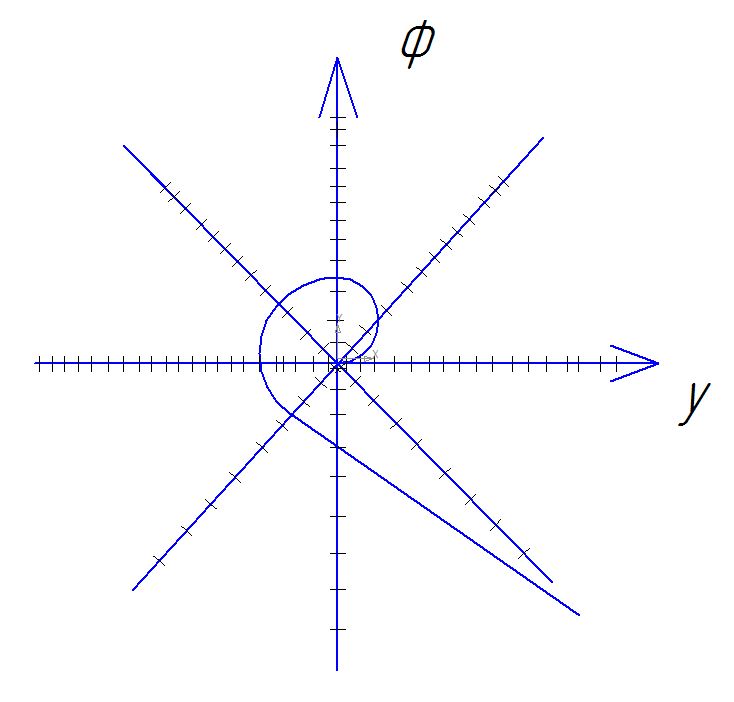
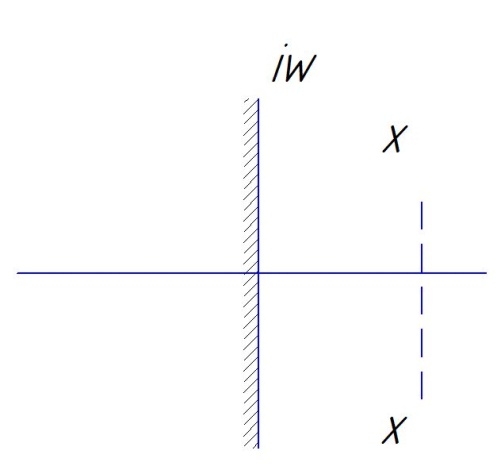
С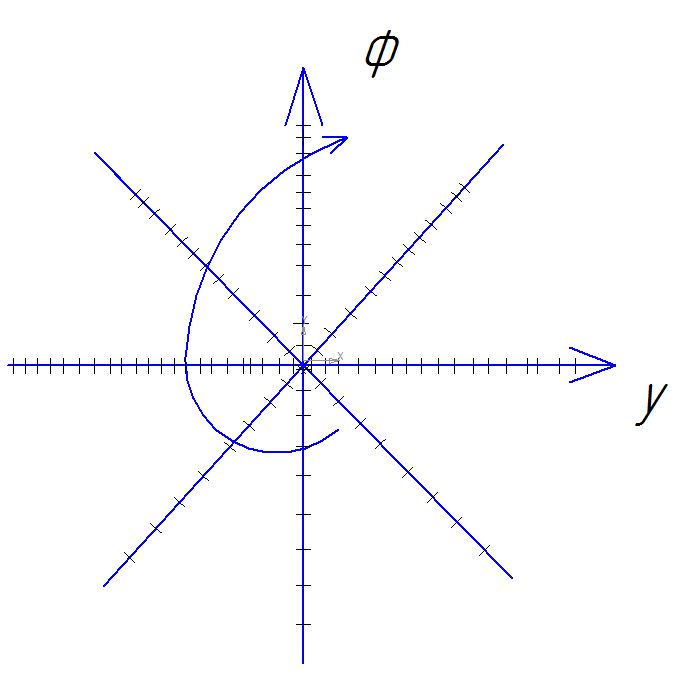
другим знаком.
С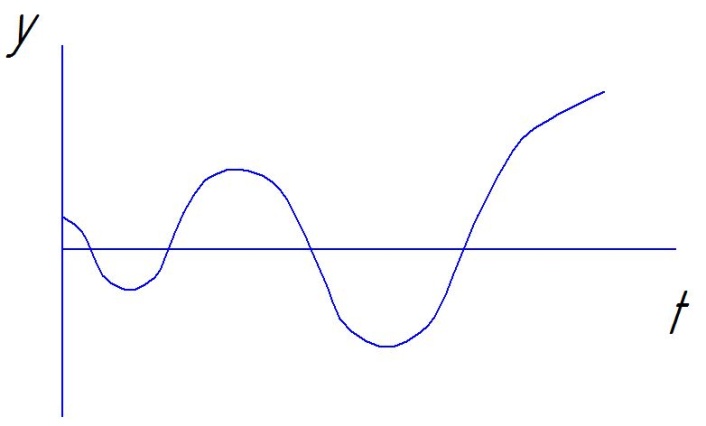
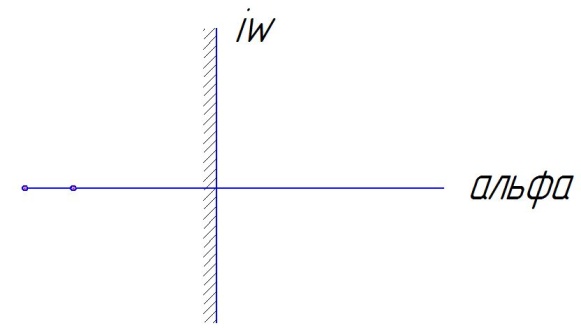
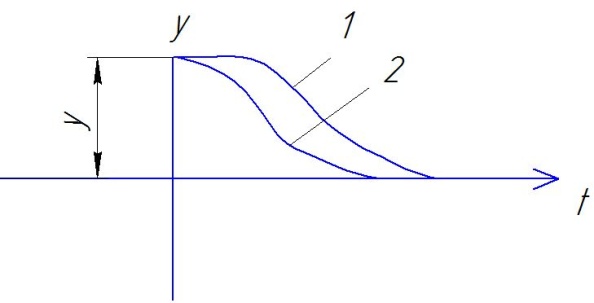истема
устойчива
Н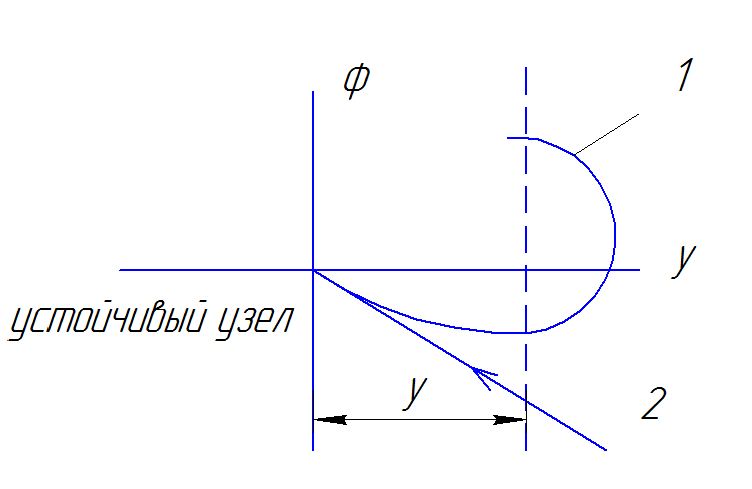
а
фазовой плоскости
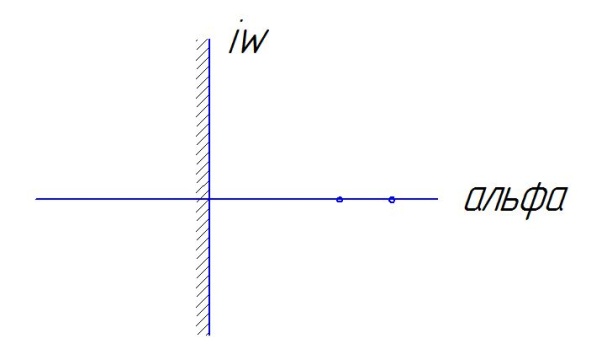
С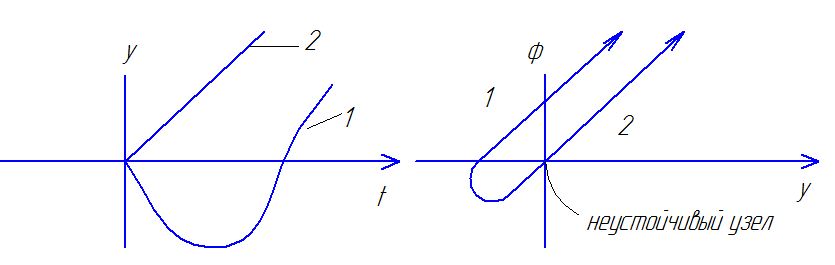
истема
неустойчива
Н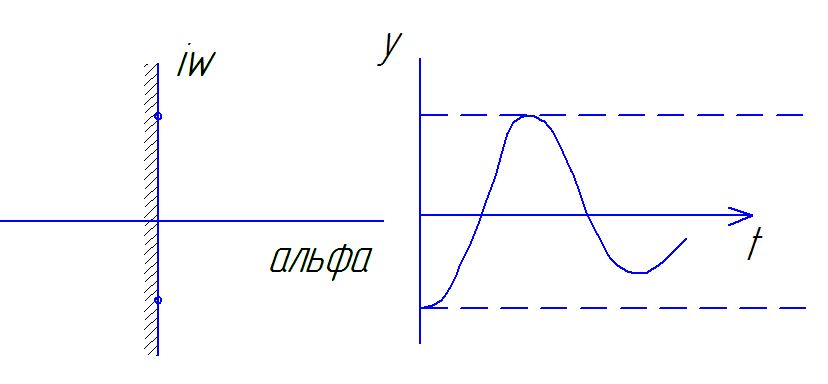
а
колебательной границе устойчивости
Решение:
-
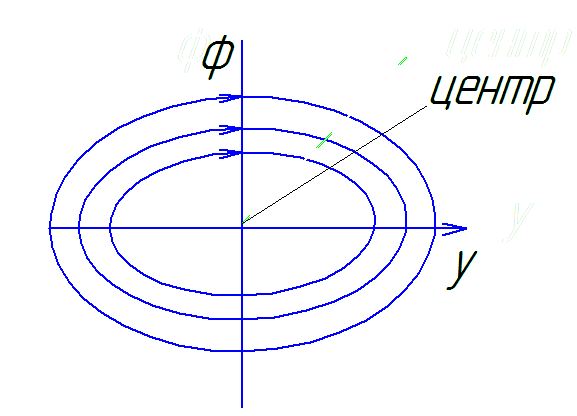семейство эллипсов
Правило направлений фазовых траекторий
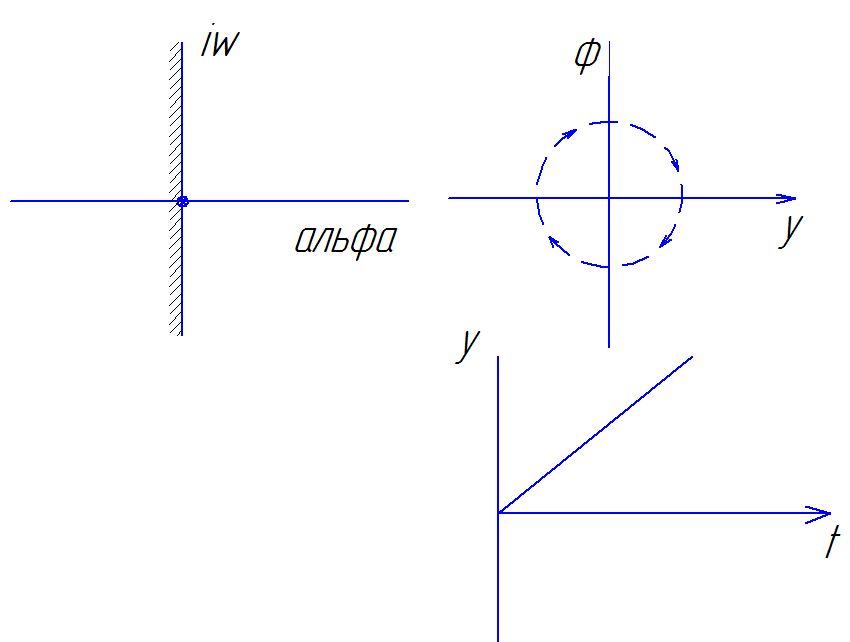
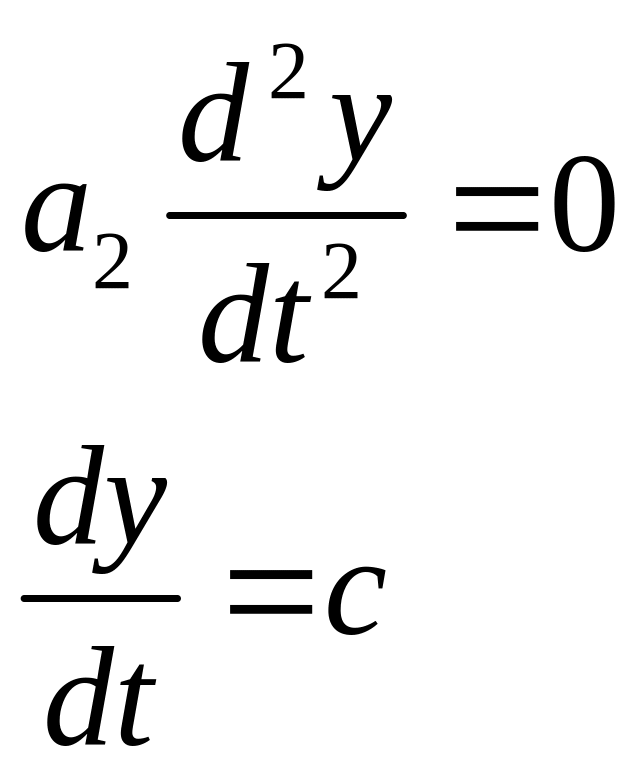
Ф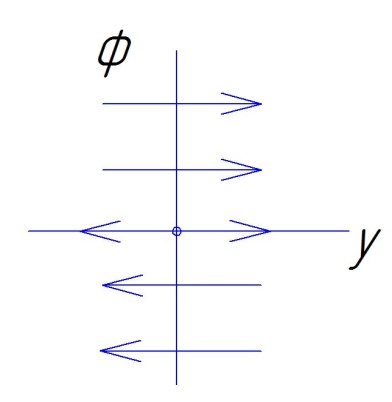
азовая
траектория
Особая точка без названия.
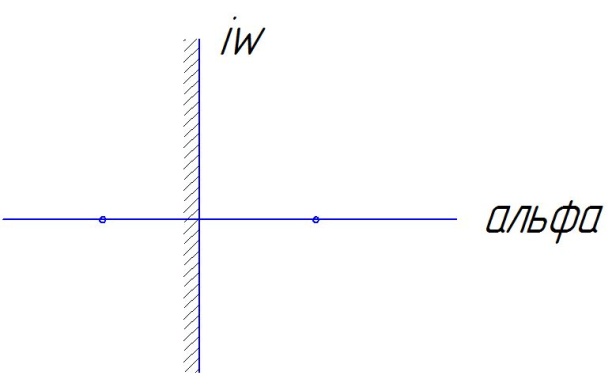
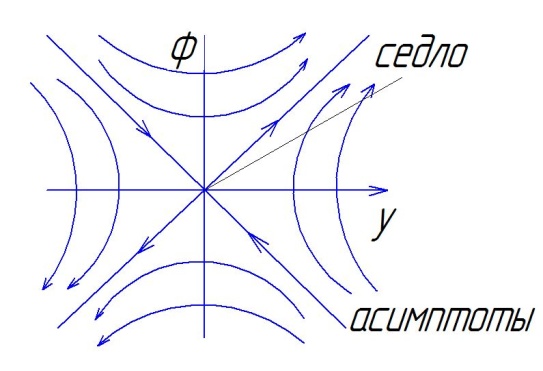
Решение
(гиперболы)
С=0: найдём уравнение асимптоты.
(В этом случае она может быть устойчива)
… - особая кривая разделяющая области с разными фазовыми траекториями.
Фазовые траектории нелинейных систем.
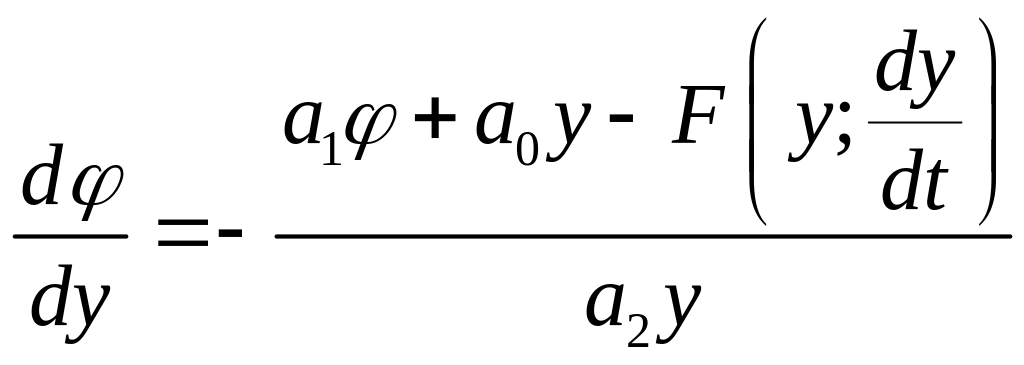(вся нелинейность справа).
в начале координат.
О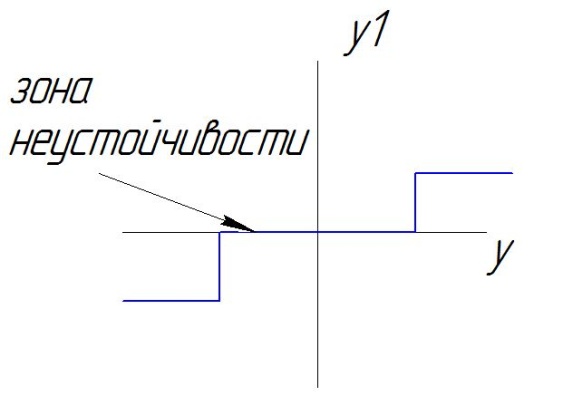
собенности
изображения на фазовой плоскости в
нелинейных системах.
с
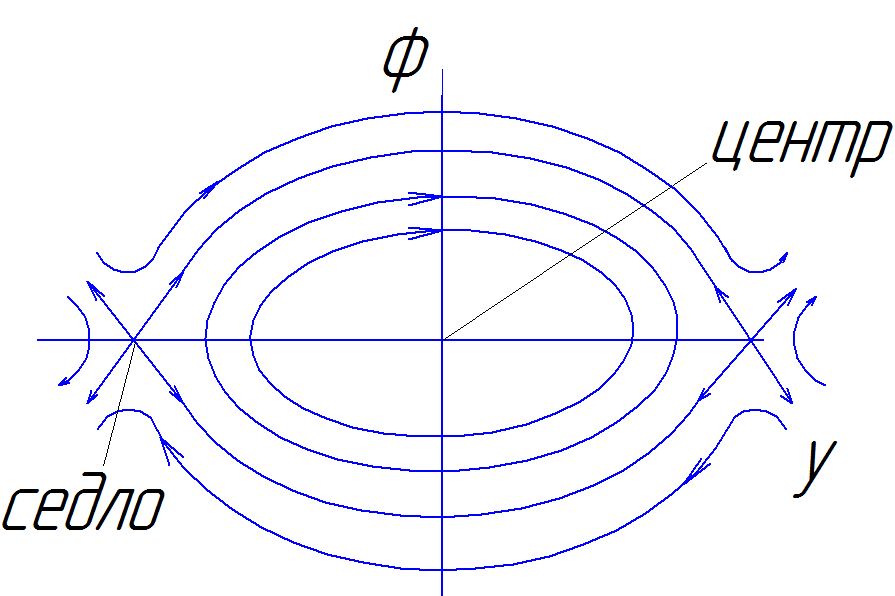емейство
узлов в зоне неустойчивости.
2)
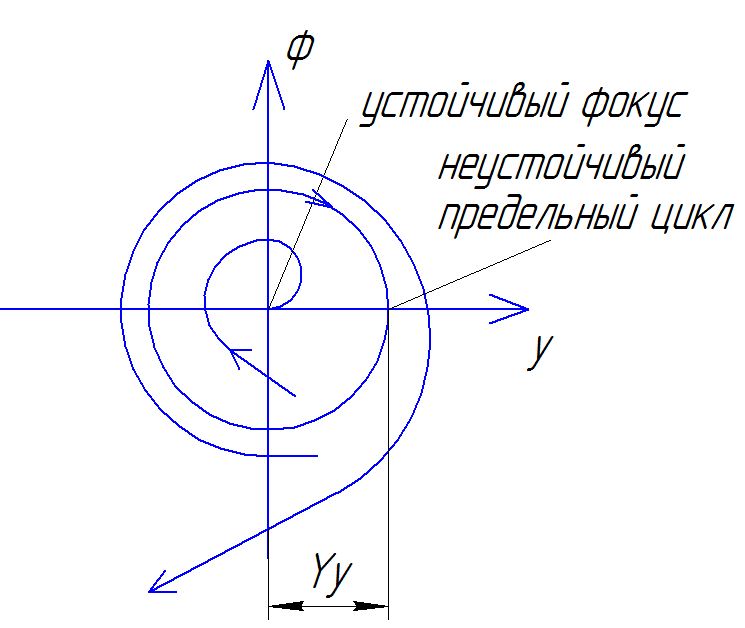
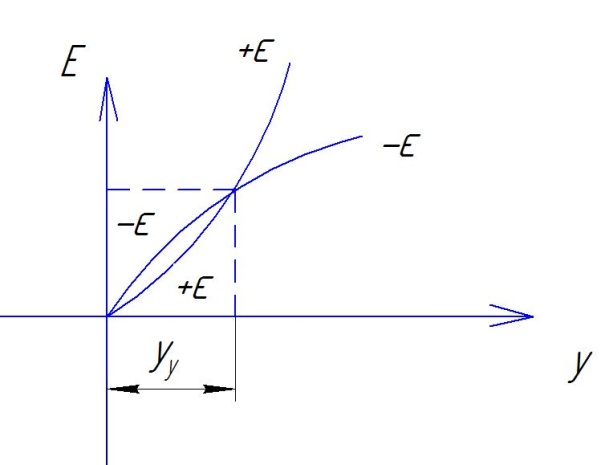
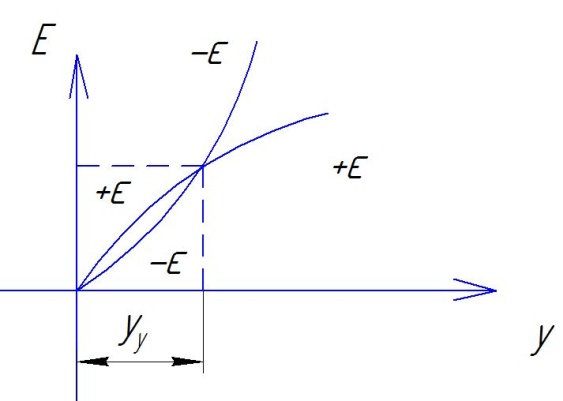
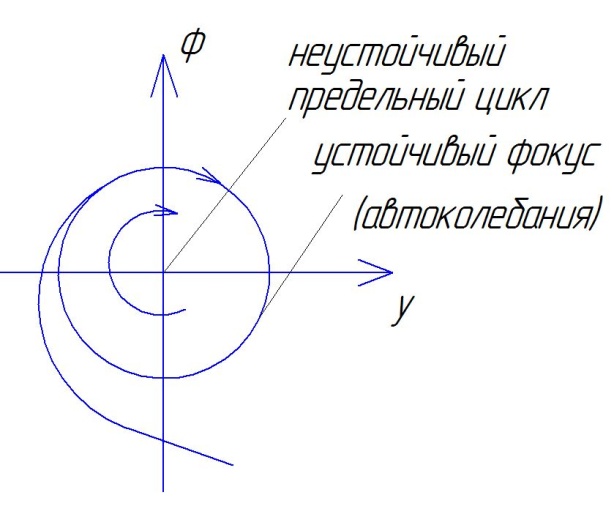
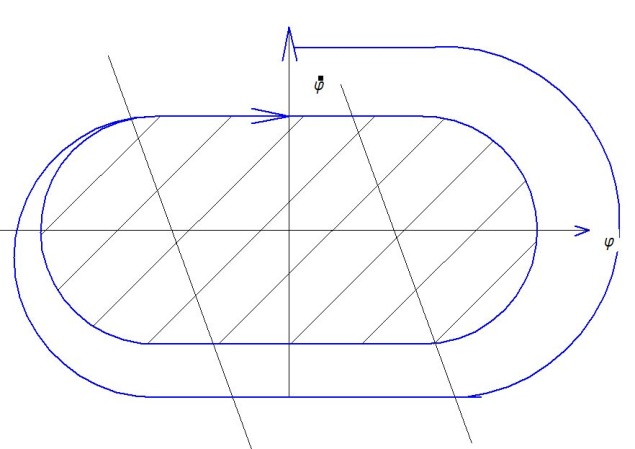
В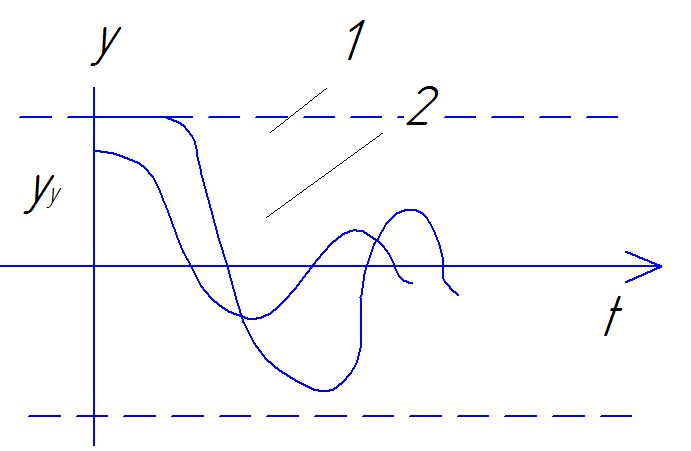
ывод:
При малых отклонениях система устойчива
,при больших неустойчива. Установившееся
от неустановившегося отличает предельный
цикл.
Всё сходится к предельному циклу.
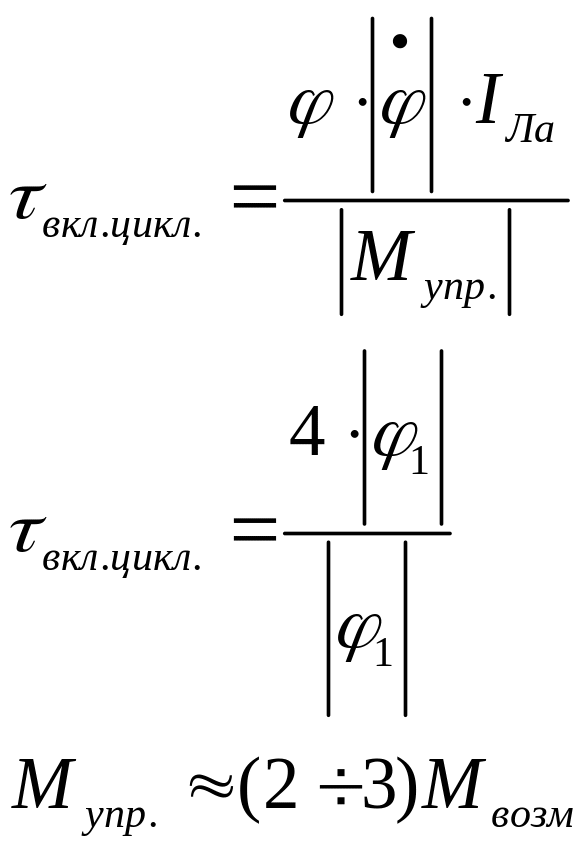
Условие возникновения колебаний:
К системе подводится энергия.
Наличие в системе нелинейности.
С
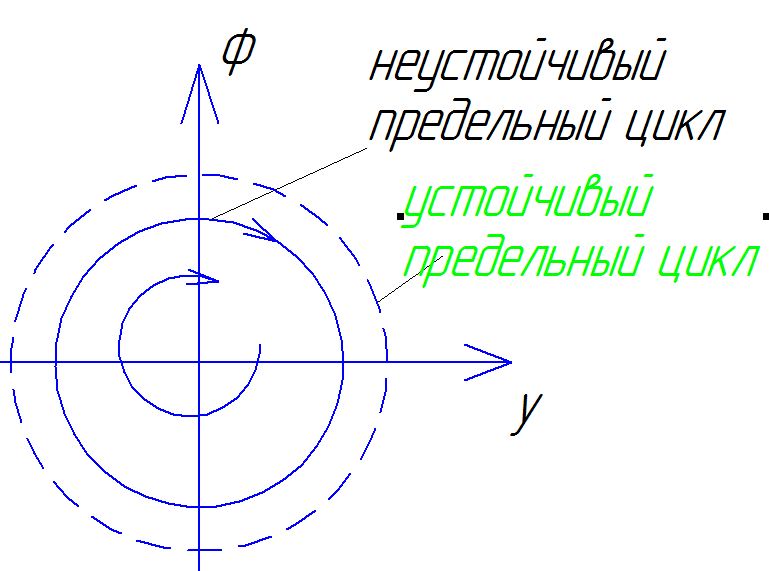
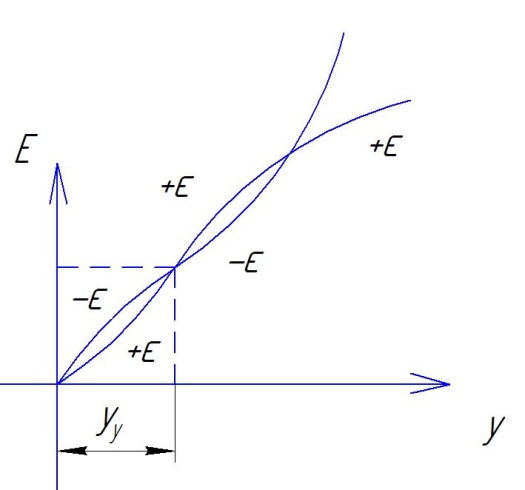вязь
между вх. и вых. параметрами.
Ж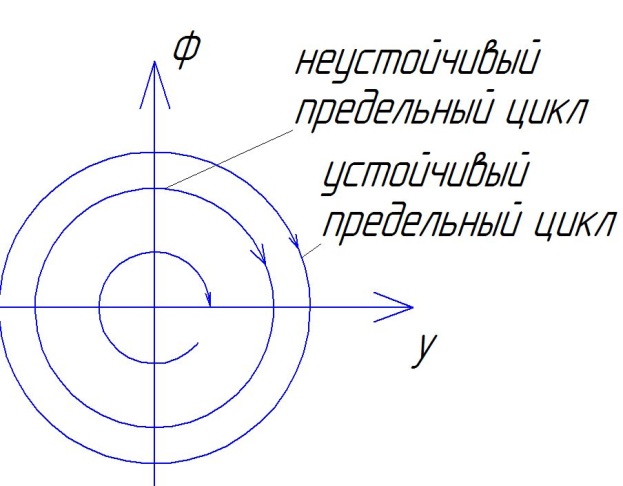
есткие
возбуждающие автоколебания происходят
при больших отклонениях.
Лекция № 13.
Р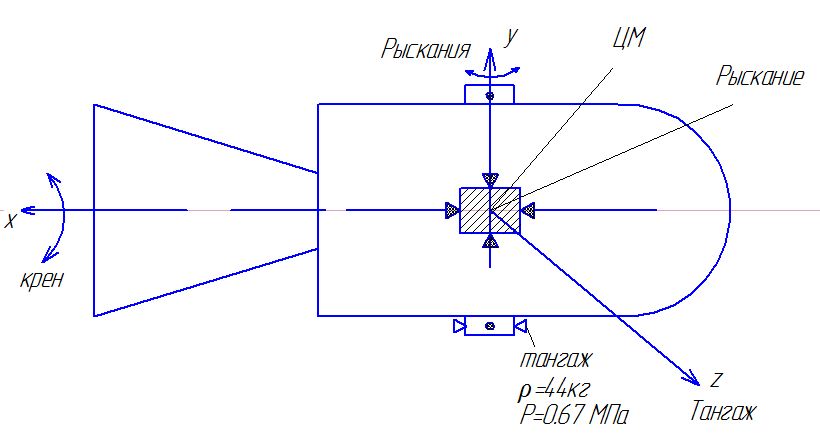
елейная
система управления космическим
летательным аппаратом относительно
центра масс.
700 МПа
Крен: (x) Допущения: 1) Не будем учитывать другие оси.
Абсолютно упругое тело.
Момент создаётся парой двигателей.
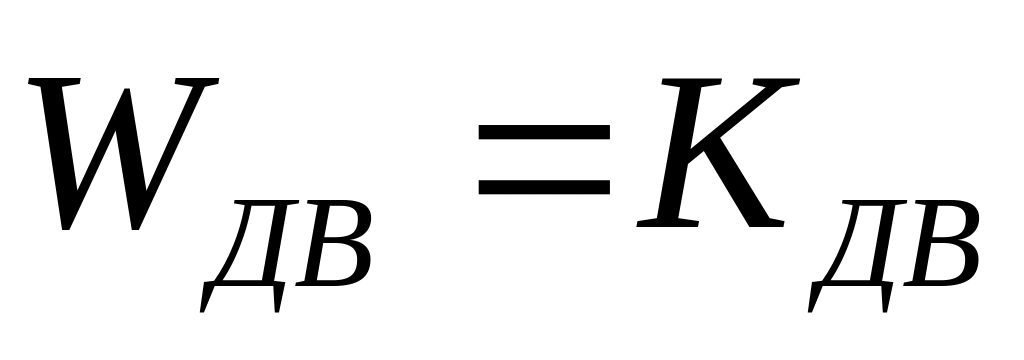
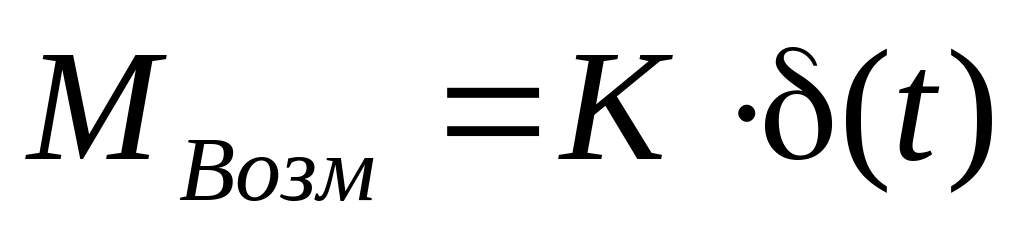
момент
инерции.
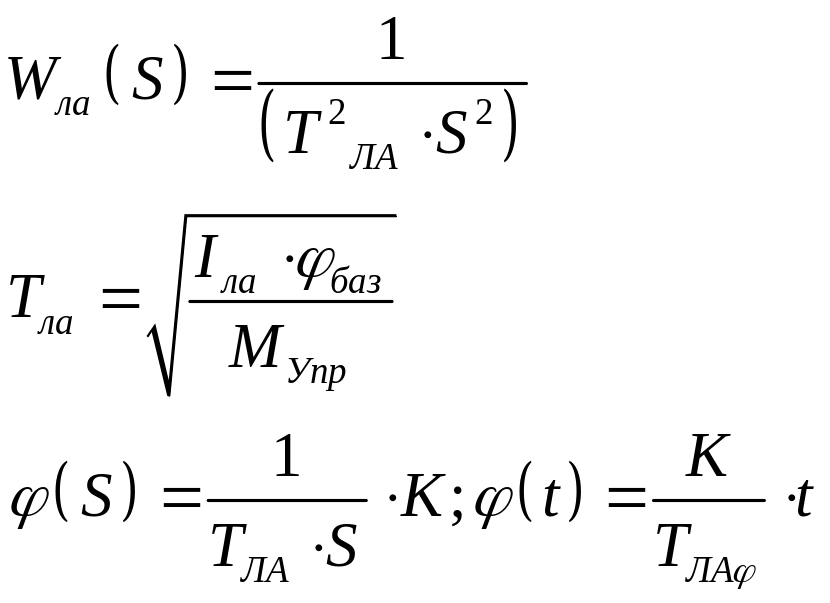
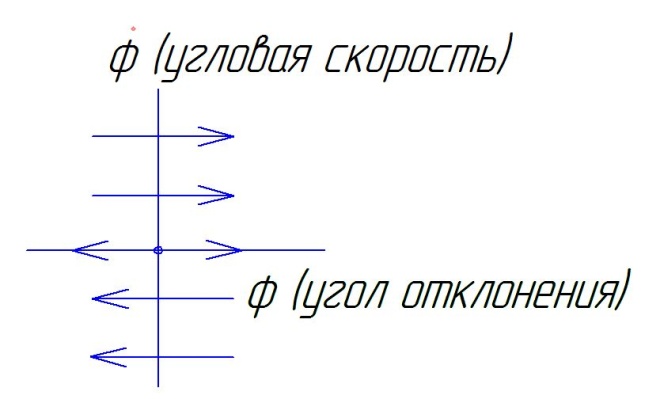
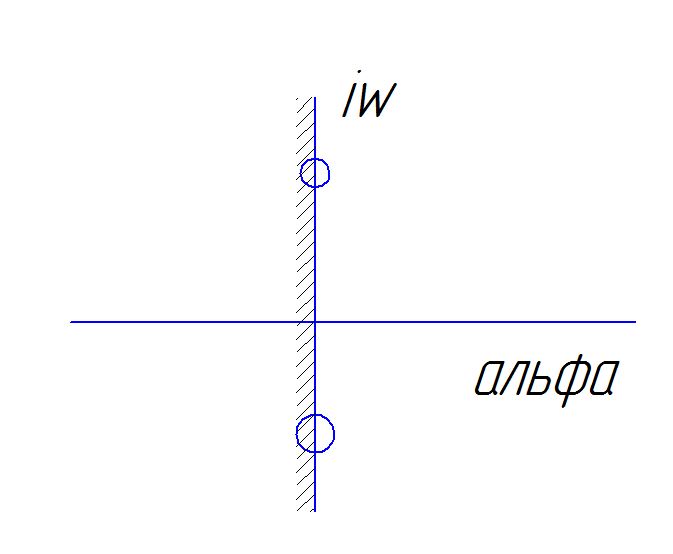
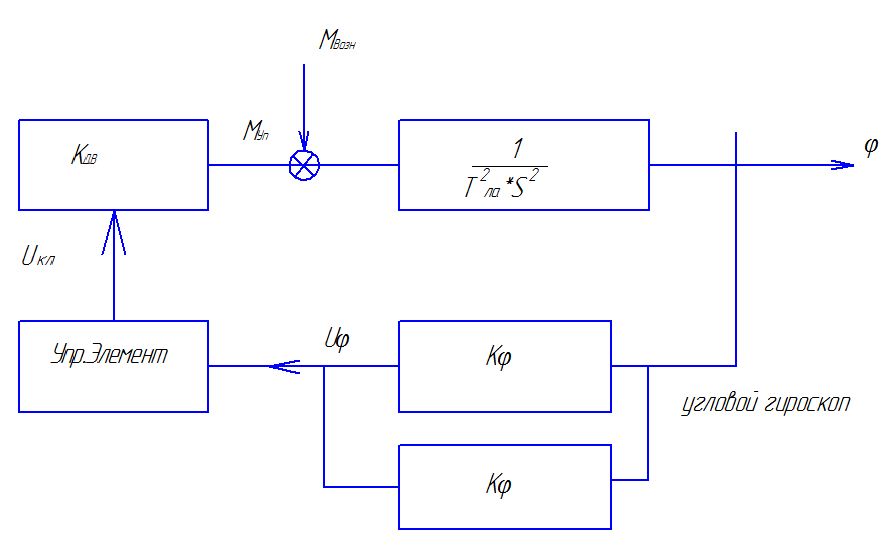
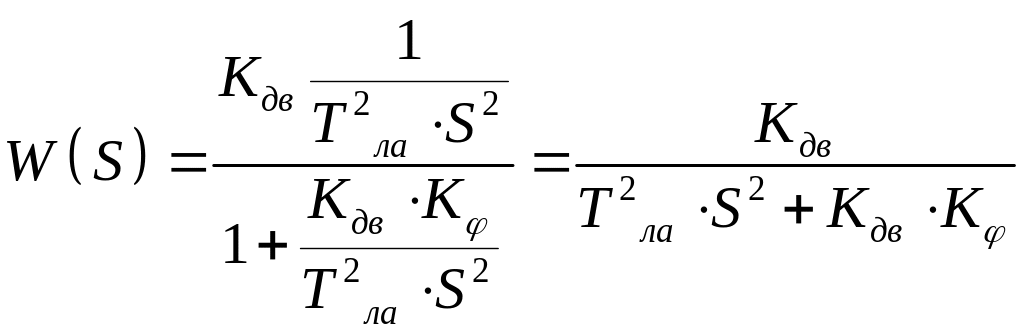
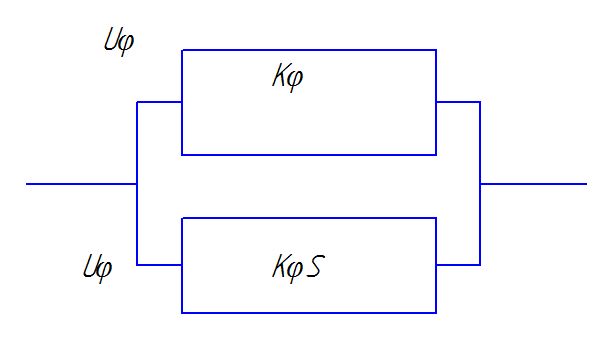
Добавим демпфирующее устройство.
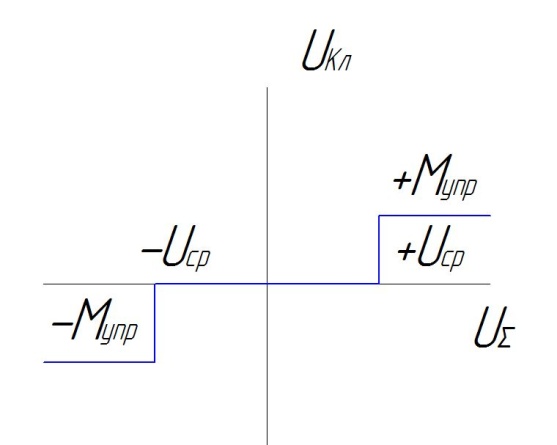
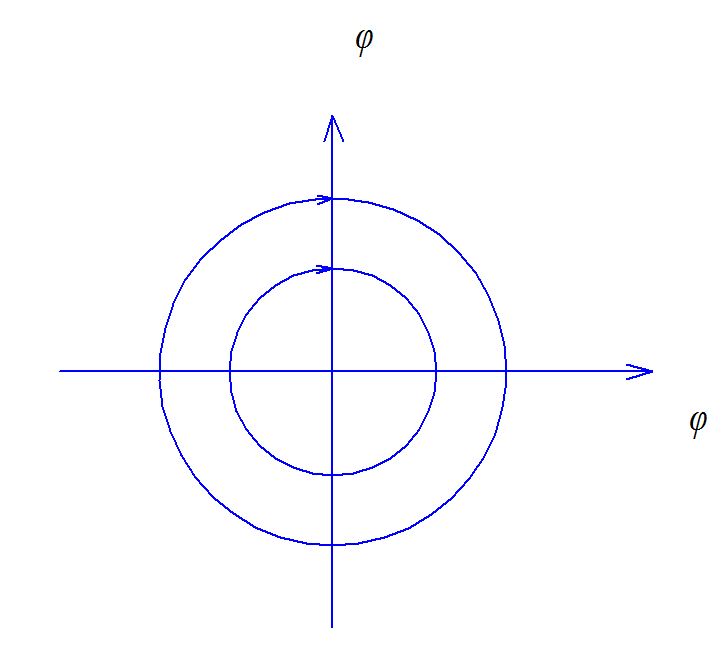
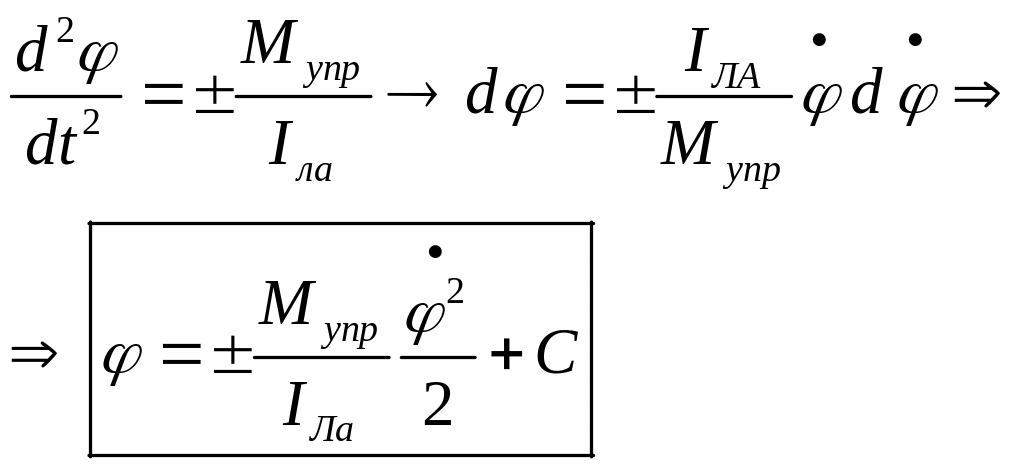
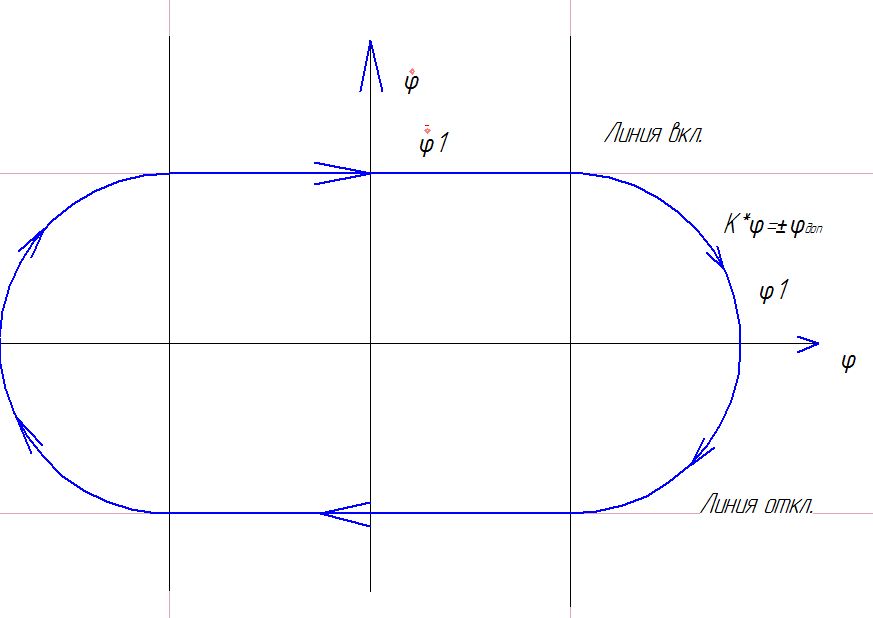Парабола.
