Лекция №4
Частотные характеристики:
Заменим
,
тогда
Отдельно выделим действительную и мнимую часть:
действ. (u) мнимая (v)
Амплитудо-частотная характеристика:
Фазо-частотная характеристика:
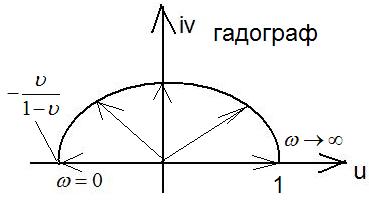
При
При
Амплитудо-частотная характеристика
Если
Логарифмические частотные характеристики.
Для РДТТ произведение заменяют суммой:
Рассмотрим АЧХ.
Децибел=1/10 бела
Единица измерения десятичного логарифма коэффициента (k) мощности сигнала.
Декада – это удесятеренное значение частоты.
Октава – это удвоенное значение частоты.
Пример: инерционное звено 1 порядка.
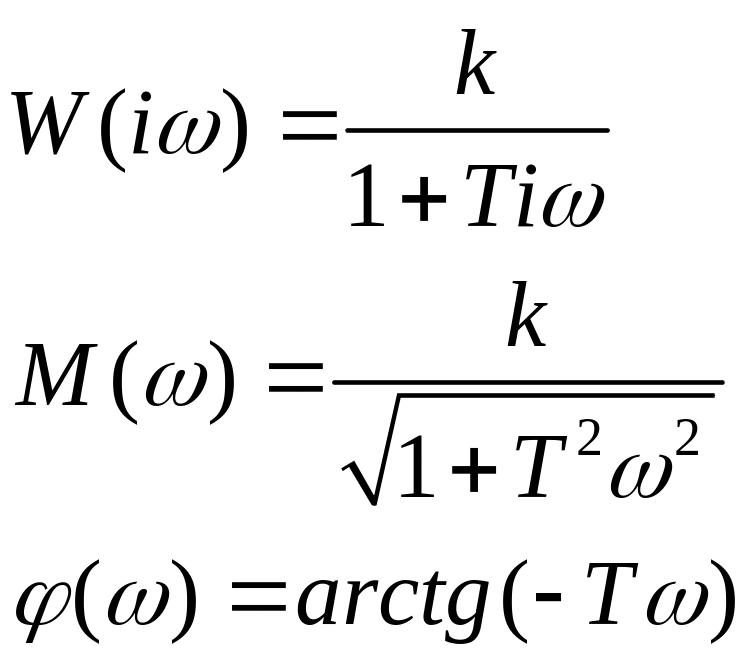
Заменяем поточечное построение частотной характеристики на касательное:
При
и
Увеличим частоту на декаду, т.е. в 10 раз.
-уменьшилась
на
,
т.е. на 20 дб на декаду.
Точка пересечения:
-сопряженная
частота
Посмотрим, наскока мы ошибаемся:
Рассмотри в логарифмических координатах:
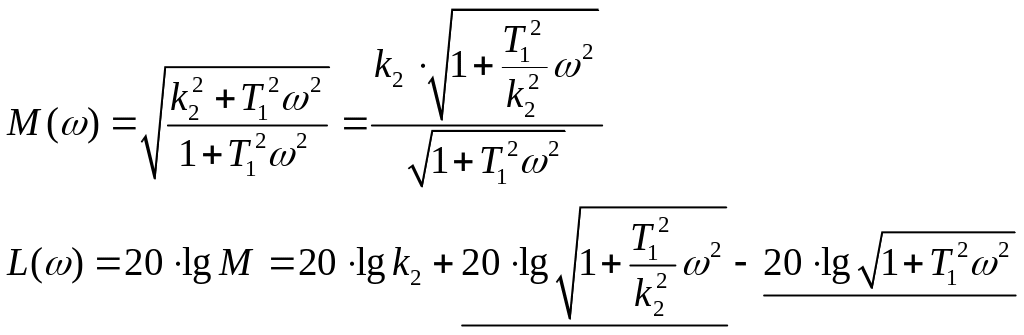
+20 дб./дек. -20 дб./дек.
Первый излом
При
|
|
|
|
|
0.2 |
0.25 |
-0.61 |
0.2/А |
0.8/А |
0.5 |
1 |
0 |
- |
- |
0.8 |
4 |
0.6 |
0.8/А |
0.2/А |
прямая +20 дб/декаду
Находим сопрягающую частоту:
-первая
сопрягающая частота
-
вторая сопрягающая частота
Лекция №5.
Критерий Найкреста.
Логарифмические частотные характеристики.
(Разомкнутая система)
АФЧХ
система
обладает запасом по устойчивости
Анализ работы ДУ.
Пример: РДТТ
Т1-постоянная времени
Из уравнения состояния газа:
Переходная функция:
Смесевое топливо:
Баллиститное топливо:
Что будет при
Возмущающее воздействие:
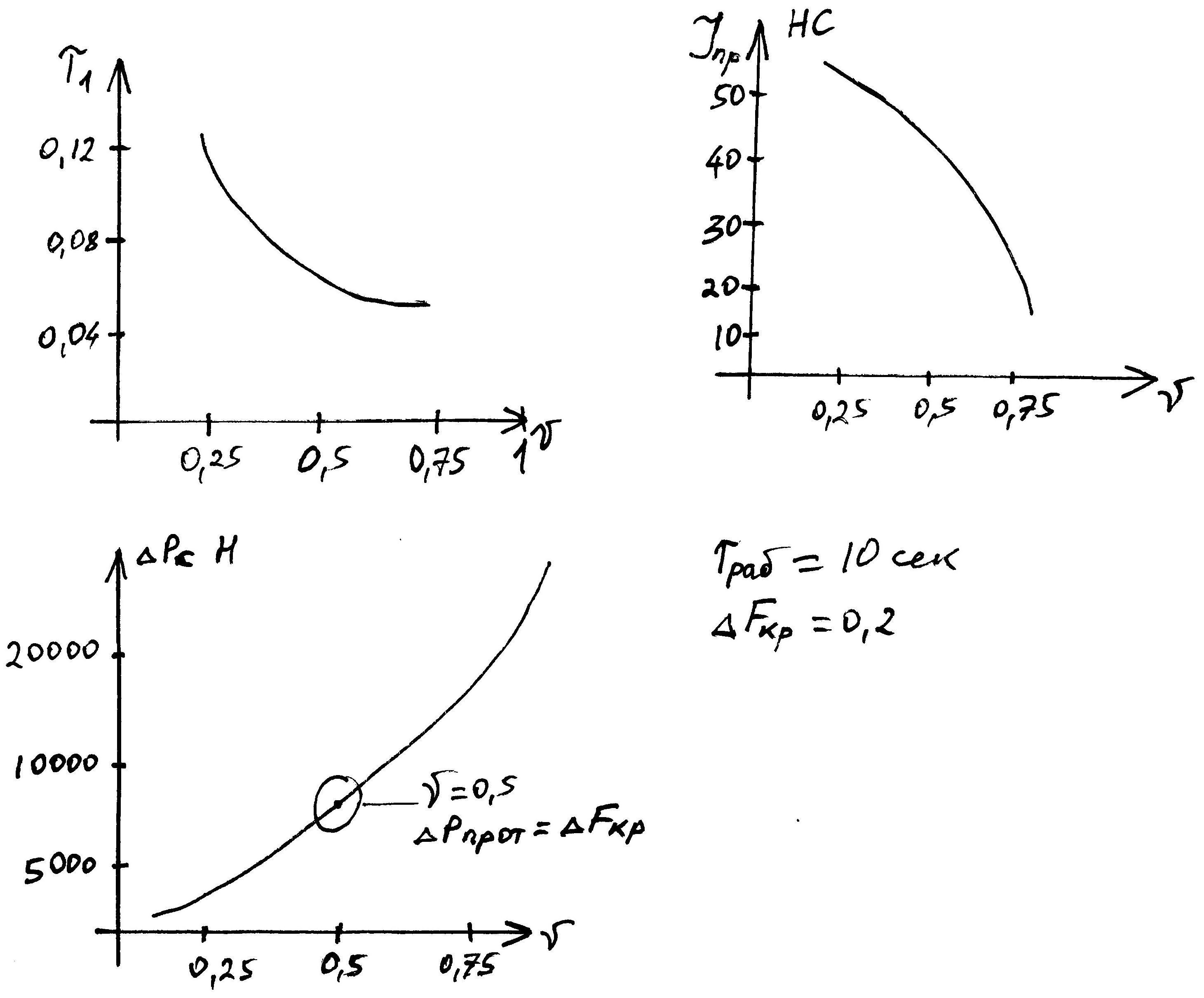
Лекция № 6.
САР с регулятором прямого действия.
Объект регулирования РДТТ.
Р
асположение
центрального тела.
2)
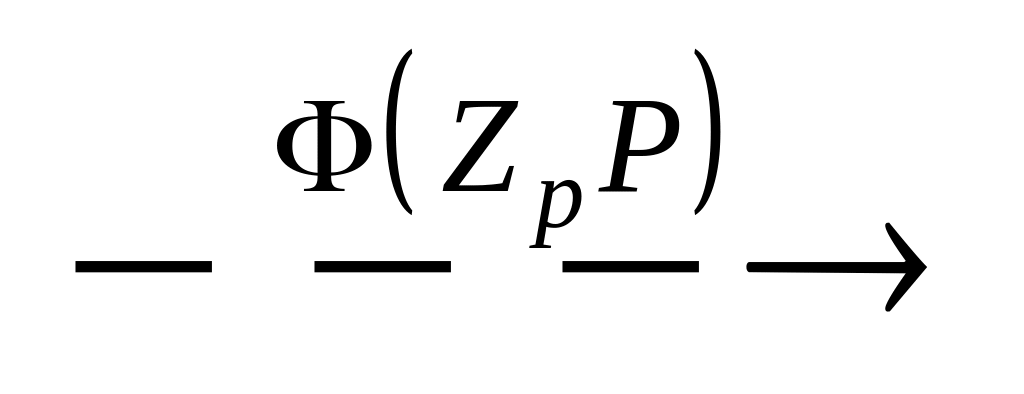
У
словие
установившегося режима.
В ряд Тейлора: m-масса регулятора. К- коэффициент трения.
Делим на
и
умножаем на
.
И
нерционное
звено 2 порядка.
,
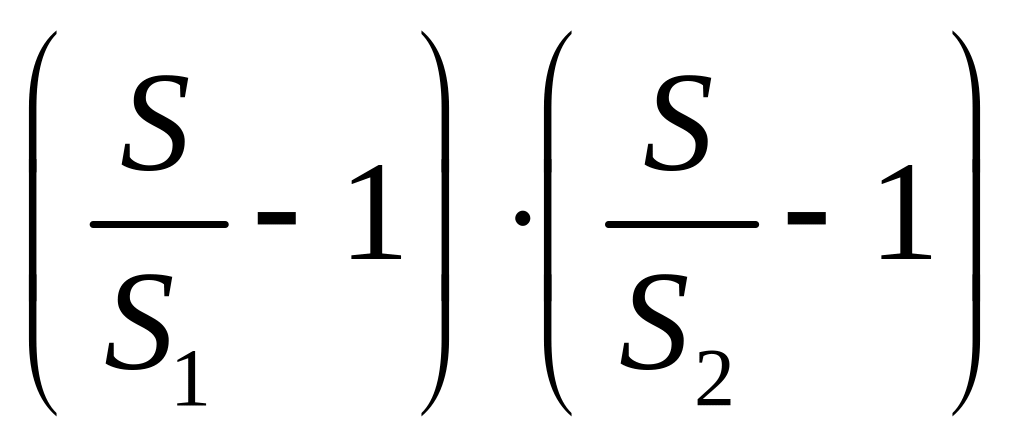
1)
корн. действ. аппериод. Процесс.
2)
апериод.
Процесс.
3)
корни мнимые. Колеб. процесс.
1.
2.
3.
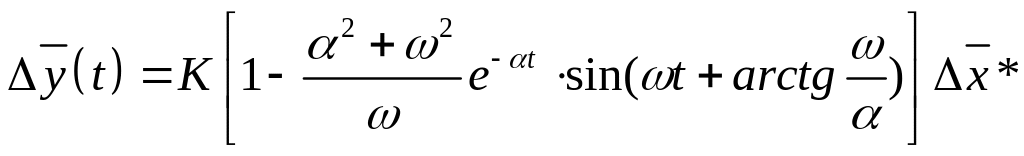
Ч
Частотные характеристики.
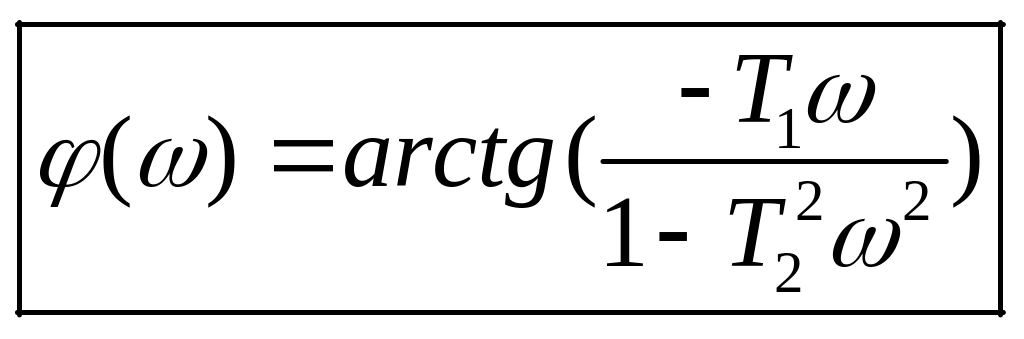
Консервативное звено:
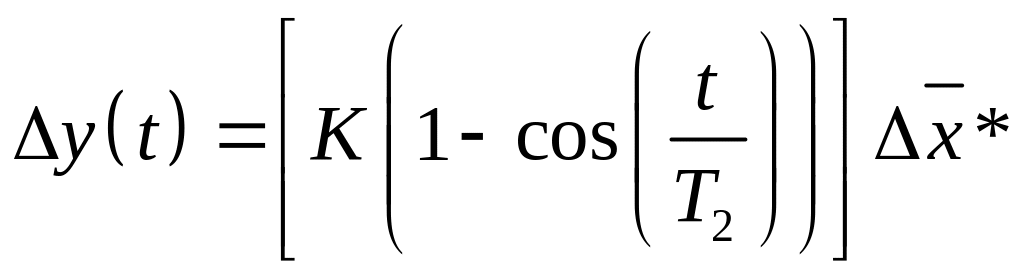
Частотные характеристики:
V=0
Объект регулирования:
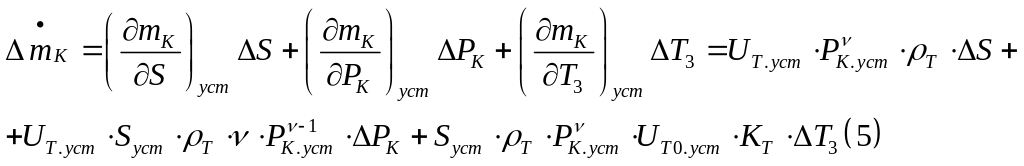
3,4,5 подставляем во 2.
Приводим всё к безразмерному виду.
Математическая модель.
Регулятор
Структурная схема.
;
.
.