
- •События и вероятность
- •Теоремы сложения и умножения вероятностей
- •Формула полной вероятности и формула Байеса
- •Повторные испытания
- •Случайные величины и законы их распределений
- •Из урны достают два шара. Случайная величина х – количество черных шаров, которые достали из урны. Ряд распределения случайной величины х имеет вид:
- •Случайная величина х задана законом распределения
- •Интегральная и дифференциальная функции распределения случайной величины
Формула полной вероятности и формула Байеса
В первом ящике 7 красных и 9 синих шаров, во втором – 4 красных и 11 синих. Из произвольного ящика достают один шар. Вероятность того, что он красный равна …
1) |
|
2) |
|
3) |
|
4) |
|
В первой урне 4 черных и 6 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
1) |
0,45 |
2) |
0,15 |
3) |
0,4 |
4) |
0,9 |
Событие А может наступить лишь при условии появления одного из двух несовместных событий
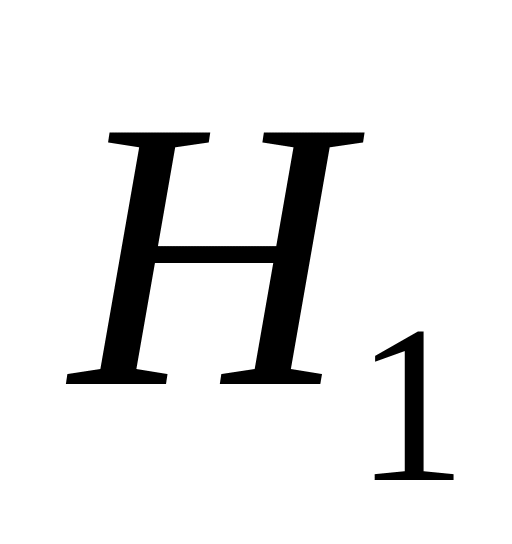 и
и
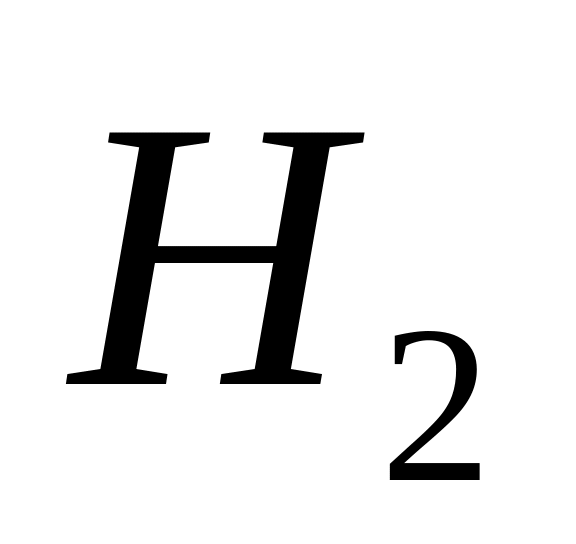 ,
образующих полную группу событий.
Известны вероятность
,
образующих полную группу событий.
Известны вероятность
 и условные вероятности
и условные вероятности
 ,
,
 .
Тогда вероятность
.
Тогда вероятность
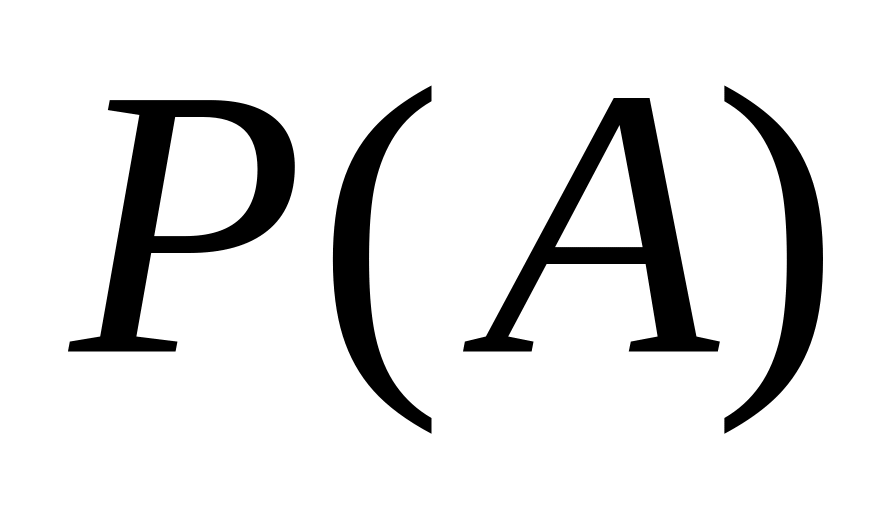 равна …
равна …
1) |
3/4 |
2) |
1/2 |
3) |
1/3 |
4) |
2/3 |
Формула полной вероятности имеет вид …
1) |
|
2) |
|
3) |
|
4) |
|
В первой урне 3 белых и 7 черных шаров. Во второй урне 1 белый и 9 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется черным, равна…
1) |
0,8 |
2) |
0,2 |
3) |
0,4 |
4) |
1,6 |
В каждой из двух урн содержится 6 белых и 4 черных шара. Из первой урны во вторую переложили один шар. Вероятность того, что шар, извлеченный из второй урны после перекладывания, окажется белым, равна…
1) |
0,2 |
3) |
0,3 |
5) |
0,4 |
7) |
0,5 |
2) |
0,6 |
4) |
0,7 |
6) |
0,8 |
8) |
0,9 |
Формула Байеса имеет вид …
1) |
|
2) |
|
3) |
|
4) |
|
В первой урне 4 белых и 6 черных шаров, во второй урне 8 белых и 2 черных шара. Из наугад выбранной урны достали белый шар. Вероятность того, что белый шар достали из первой урны равна …
1) |
0,4 |
3) |
0,6 |
5) |
0,8 |
2) |
1/3 |
4) |
2/3 |
|
|
Если произошло событие А, которое может появиться только с одной из гипотез Н1, Н2, …, Hn образующих полную группу событий, то произвести количественную переоценку априорных (известных до испытания) вероятностей гипотез можно по …
1) |
Формуле полной вероятности |
4) |
Формуле Пуассона |
2) |
Формуле Байеса |
5) |
Формуле Муавра-Лапласа |
3) |
Формуле Бернулли |
|
|
Событие А может наступить лишь при условии появления одного из трех несовместных событий , ,
 ,
образующих полную группу событий.
Известны вероятности:
,
образующих полную группу событий.
Известны вероятности:
 ,
,
 ,
,
,
,
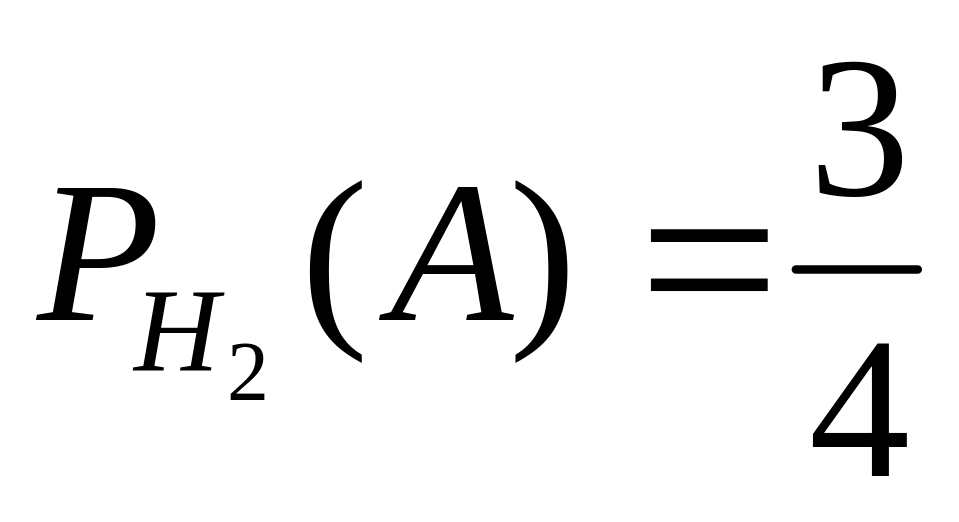 и
и
 .
Установите соответствие
.
Установите соответствие
А) |
P(A) |
1) |
2/9 |
В) |
|
2) |
1/9 |
C) |
|
3) |
9/16 |
D) |
|
4) |
7/16 |
|
|
5) |
2/3 |
|
|
6) |
1/3 |
