Длина кривой.

Пусть имеется кривая АВ. Возьмем на АВ ряд точек, следующих друг за другом вдоль кривой: M₀=A, M₁,…,M_n-1,M_n=B. Соединяя последовательно эти точки прямолинейными отрезками, получим некоторую ломаную линию, вписанную в кривую АВ.

Рисунок.

Обозначим через длину i-го звена ломаной. Тогда l_лом.= будет длиной ломаной.

Для закрепленного числа n и для закрепленного способа выбора точек M₁,М₂,…,M_n-1 значение величины l_лом будет вполне определенным числом. Если же число точек M₁,М₂,…,M_n-1 и способы их выбора на кривой АВ менять, то меняться и значение величины l_лом.

Положим = .

Определение. Если существует конечный предел длины вписанной в дугу ломаной

l= (1)

не зависящий от способа выбора вершин ломаной, то этот предел называют длиной дуги АВ, а саму дугу АВ называют в этом случае спрямляемой.

Длина дуги кривой, заданной явным уравнением.

Теорема 1. Пусть кривая АВ задана явным уравнением y=f(x), x[a,b], a<b

Пусть функция f(x) имеет в промежутке [a,b] непрерывную производную . Тогда кривая АВ спрямляема, и ее длина равна:

l= (2)

Доказательство. Введем обозначение: y_i=f(x_i+1)-f(x_i).

Тогда длина =l_i= =

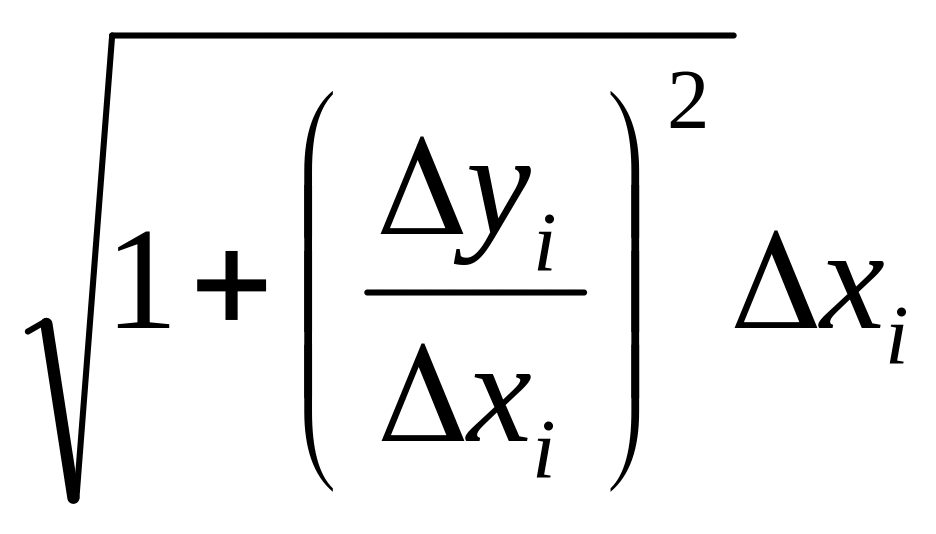
По теореме Лагранжа имеем: = , где .

Следовательно, l_i= .

Т.о. длина вписанной ломаной l_лом.= .

По условию, непрерывна, следовательно, функция тоже непрерывна. Поэтому существует предел l= и при этом

l= = или l= (3) ч.т.д.

Пример.

Длина дуги, заданной параметрически.

Теорема 2. Пусть дуга АВ задана параметрически уравнениями

Пусть функции (t) и (t) имеют в промежутке [,] непрерывные производные и . Тогда кривая АВ спрямляема, и ее длина равна:

l= (4)

Доказательство. Пусть а=(), b=(). Сделаем в интеграле (3) подстановку х=(t), dx= dt, получим и

l=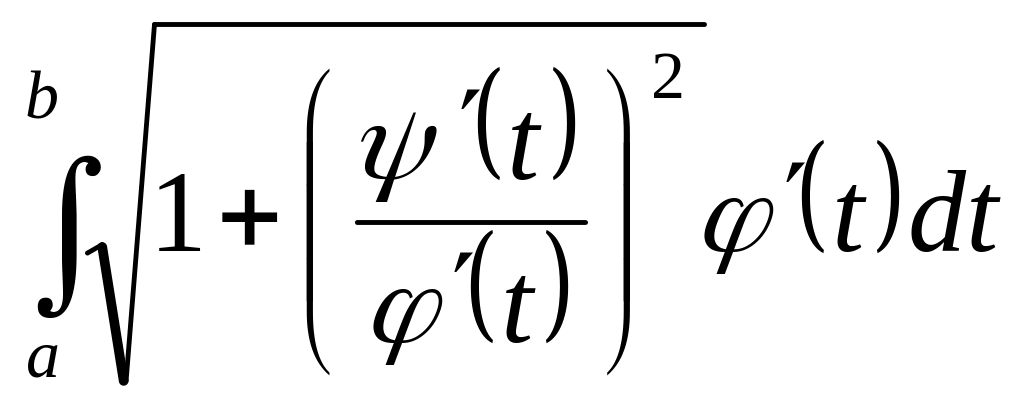 или l= ч.т.д.

Пример.

Длина дуги кривой в полярных координатах.

Теорема 3. Пусть дуга АВ задана уравнением r=f(), [,], <.

Пусть функция r=f() имеет в промежутке [,] непрерывную производную . Тогда кривая АВ спрямляема, и ее длина равна:

l= (5)

Доказательство. Т.к. , то параметрическое уравнение кривой АВ в этом случае будет: (здесь  - параметр)

Тогда 

Выполнены условия теоремы 2. Следовательно, кривая АВ спрямляема, и ее длина равна: l= ч.т.д.