Формула Ньютона-Лейбница.

Теорема. Пусть функция f(x) непрерывна на отрезке [a;b]. Пусть функция F(x) является некоторой ее первообразной на этом отрезке, тогда

=F(b)-F(a) (17)

Доказательство. По условию F(x) – первообразная для f(x) на [a;b].

Т.к. f(x) непрерывна на [a;b], то функция Ф(х)= тоже является первообразной для функции f(x). Тогда, функции Ф(х) и F(x) отличаются друг от друга в [a;b] только на постоянную величину. Т.е. Ф(х)-F(x)=С или =F(x)+С

Положим в последнем тождестве х=а, тогда

=F(а)+СС=-F(а)

Тогда =F(x)-F(а)

Полагая х=b, получим =F(b)-F(а) ч.т.д.

=F(х) = F(b)- F(а)

Пример. 1) , 2)

Замена переменной в определенном интеграле.

Теорема. Пусть функция f(x) непрерывна на отрезке [a;b]. Тогда если

1. функция x=φ(t) определена на [α;β] и имеет там непрерывную производную φ΄(t);

2. множеством значений функции x=φ(t) является отрезок [a;b];

3. φ(α)=a и φ(β)=b, то справедлива формула

(18)

Доказательство. Пусть F(х) – первообразная для функции f(x).

По формуле Ньютона-Лейбница =F(b)-F(a)

F΄(x)=f(x), F΄(φ(t))=F΄(φ(t))·φ΄(t)=f(φ(t))·φ΄(t),

Т.е. функция F΄(φ(t)) является первообразной для функции f(φ(t))·φ΄(t).

Тогда по формуле Ньютона-Лейбница

=F(φ(β))- F(φ(α))=F(b)-F(a)= ч.т.д.

Примеры. 1)

Замена: x=r sin t, dx=r cos t dt.

Определим новые пределы: x=0 при t=0, x=r при t= . Следовательно,

= = = =

= = =

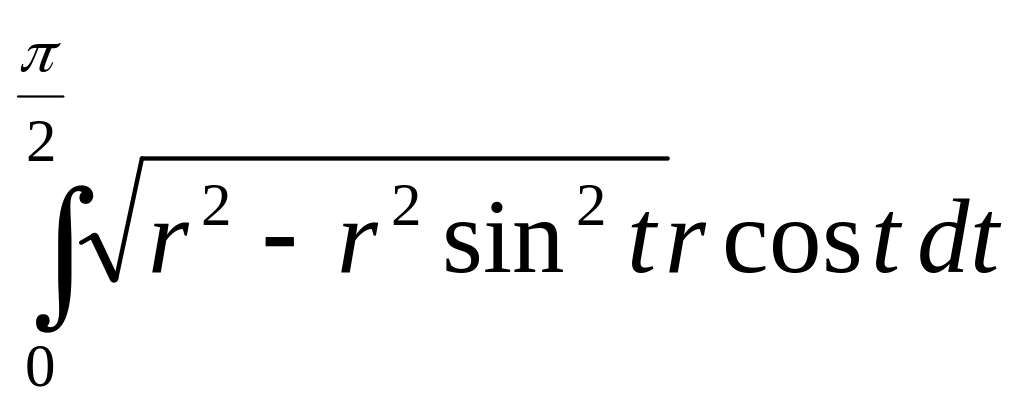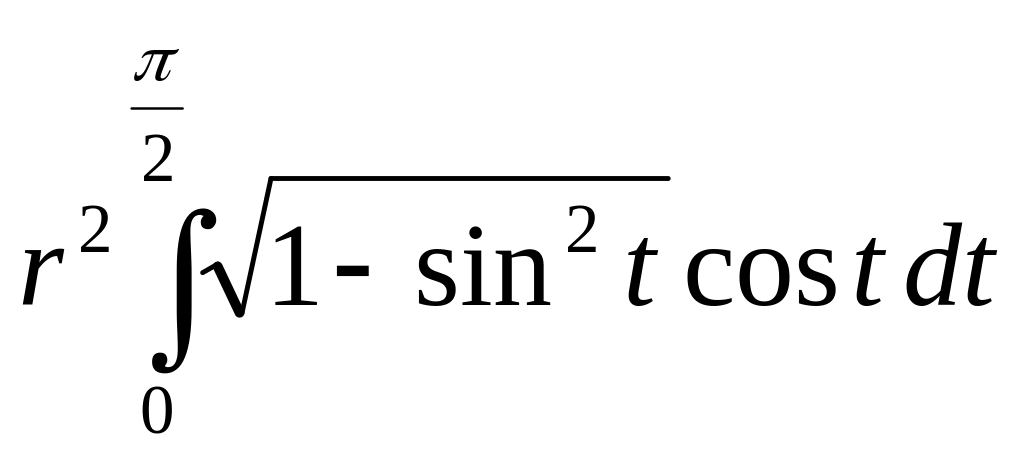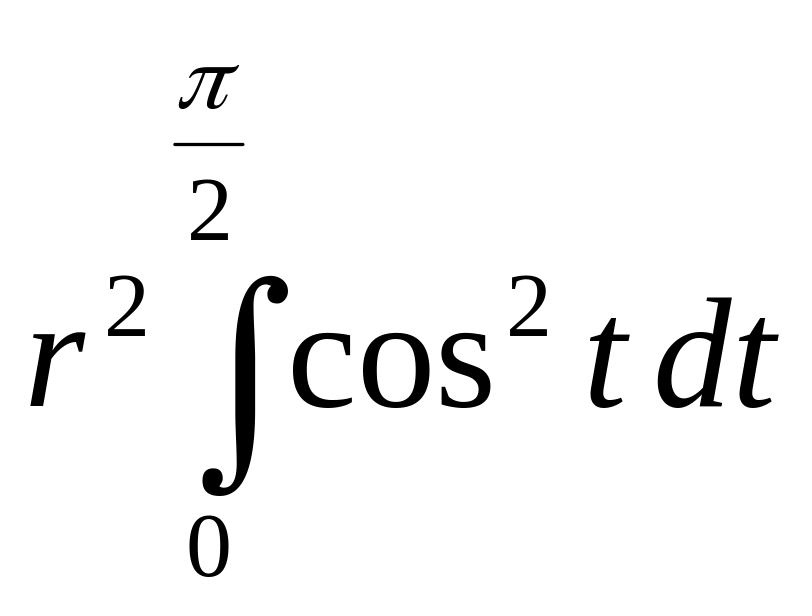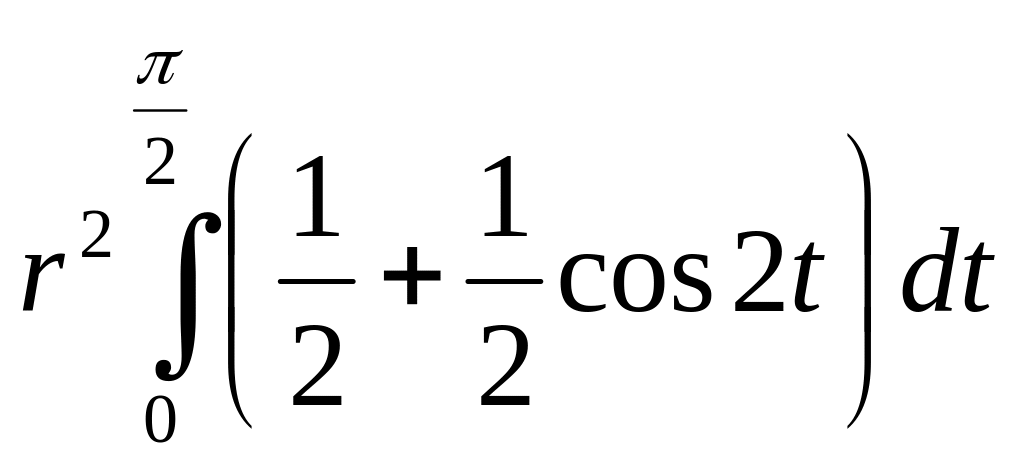Формула интегрирования по частям в определенном интеграле.

Теорема. Пусть функции u(x) и v(x) – непрерывные вместе со своими производными u΄(x) и v΄(x) на отрезке [a;b]. Тогда справедлива формула:

(19)

Доказательство. Т.к.(uv)΄=u΄v+v΄u, то функция uv является первообразной для функции u΄v+v΄u.

По формуле Ньютона-Лейбница получаем

По свойству определенных интегралов:

Отсюда ч.т.д.

Пример. 1) = = - =0- =-1-1=-2.

2) = = + =0- =

Геометрические приложения определенного интеграла.

Вычисление площадей плоских фигур.

Площадь в прямоугольных координатах.

1. Пусть функция f(x) неотрицательна и непрерывна на отрезке [a;b]. Тогда, по геометрическому смыслу определенного интеграла, площадь фигуры под кривой f(x) на [a;b] численно равна . (1)

Пример.

2. Пусть функция f(x) неположительна и непрерывна на отрезке [a;b]. Отражая кривую f(x) относительно оси Ох, получаем кривую с уравнением у= - f(x). Функция у=- f(x) неотрицательна на [a;b] и площадь фигуры под кривой у=- f(x) на [a;b] равна площади S (из соображений симметрии). S= = -

Пример.

3. Если функция f(x) конечное число раз меняет знак на отрезке [a,b], то ин6теграл по всему отрезку [a,b] разбиваем на сумму интегралов по частичным отрезкам. Интеграл будет положителен на тех отрезках, где f(x)0, и отрицателен там, где f(x)0. Интеграл по всему отрезку равен разности площадей, лежащих выше и ниже оси Ох. Для того, чтобы получить сумму площадей в обычном смысле, нужно найти сумму абсолютных величин интегралов по указанным отрезкам или вычислить интеграл

Рисунок.

Пример. Вычислить площадь фигуры, ограниченной синусоидой у=sin x и осью Ох, при 0х2.

Рисунок.

S= + =

= =-(cos  - cos 0)= - (-1-1)=2

= =-(cos 2-cos )= -2

S=2+-2=4

4. (Площадь обобщенной криволинейной трапеции). Теорема. Пусть на отрезке [a;b] заданы непрерывные функции y=f₁(x) и y=f₂(x) такие, что f₁(x)≤f₂(x). Тогда площадь фигуры, заключенной между кривыми y=f₁(x) и y=f₂(x) на отрезке [a;b]:

S= (2)

Рисунки.

Пример.